More Related Content
PDF
PDF
プログラミングコンテストでのデータ構造 2 ~動的木編~ PDF
PDF
AtCoder Beginner Contest 021 解説 PDF
PDF
プログラミングコンテストでのデータ構造 2 ~平衡二分探索木編~ PDF
PDF
What's hot
PDF
PDF
PDF
PDF
PDF
PDF
二部グラフの最小点被覆と最大安定集合と最小辺被覆の求め方 PDF
PDF
PDF
PDF
PDF
PDF
勉強か?趣味か?人生か?―プログラミングコンテストとは PDF
PPTX
PDF
PDF
PDF
Amortize analysis of Deque with 2 Stack PDF
AtCoder Beginner Contest 015 解説 PPTX
PDF
Viewers also liked
PDF
AtCoder Beginner Contest 035 解説 PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
競技プログラミングにおけるMajorization PDF
PDF
PDF
ODP
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Similar to 辺彩色
PDF
PDF
KMC 競技プログラミング練習会 Advanced 第3回 ふろー PDF
PDF
PDF
PDF
競技プログラミング練習会2015 Normal 第3回 PDF
PDF
Stochastic complexities of reduced rank regression証明概略 PPTX
More from Ken Ogura
PDF
PDF
ODP
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
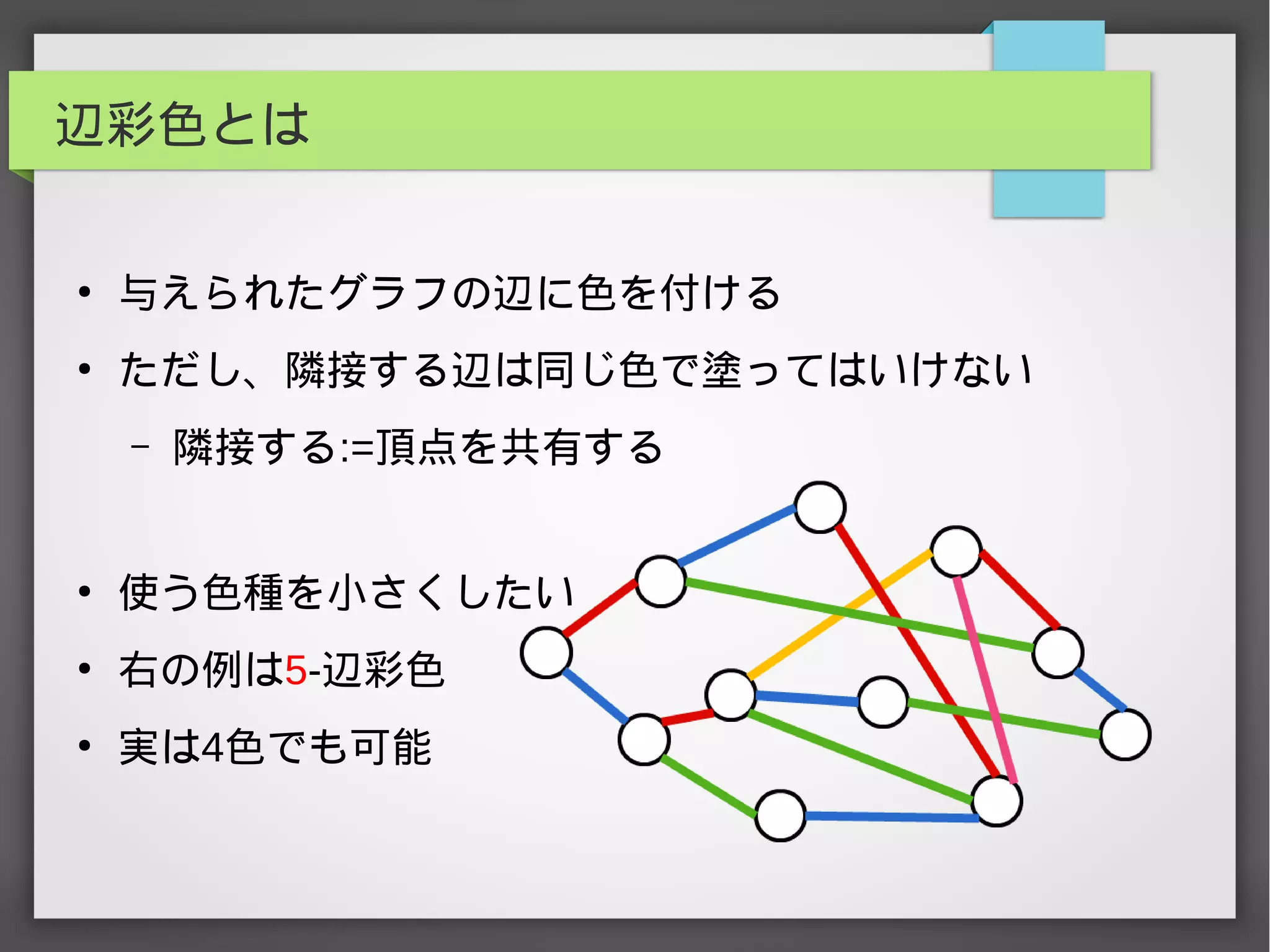
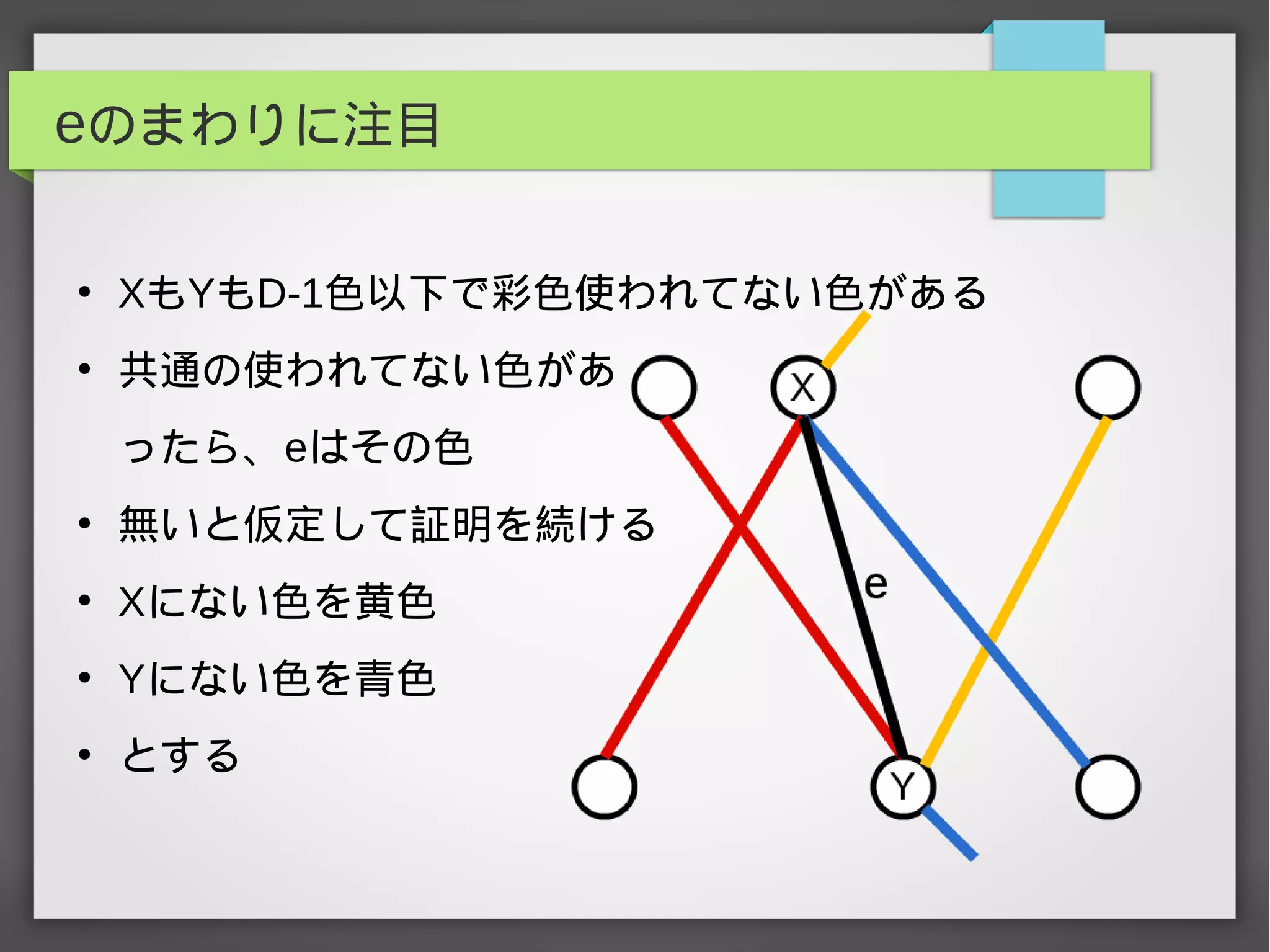
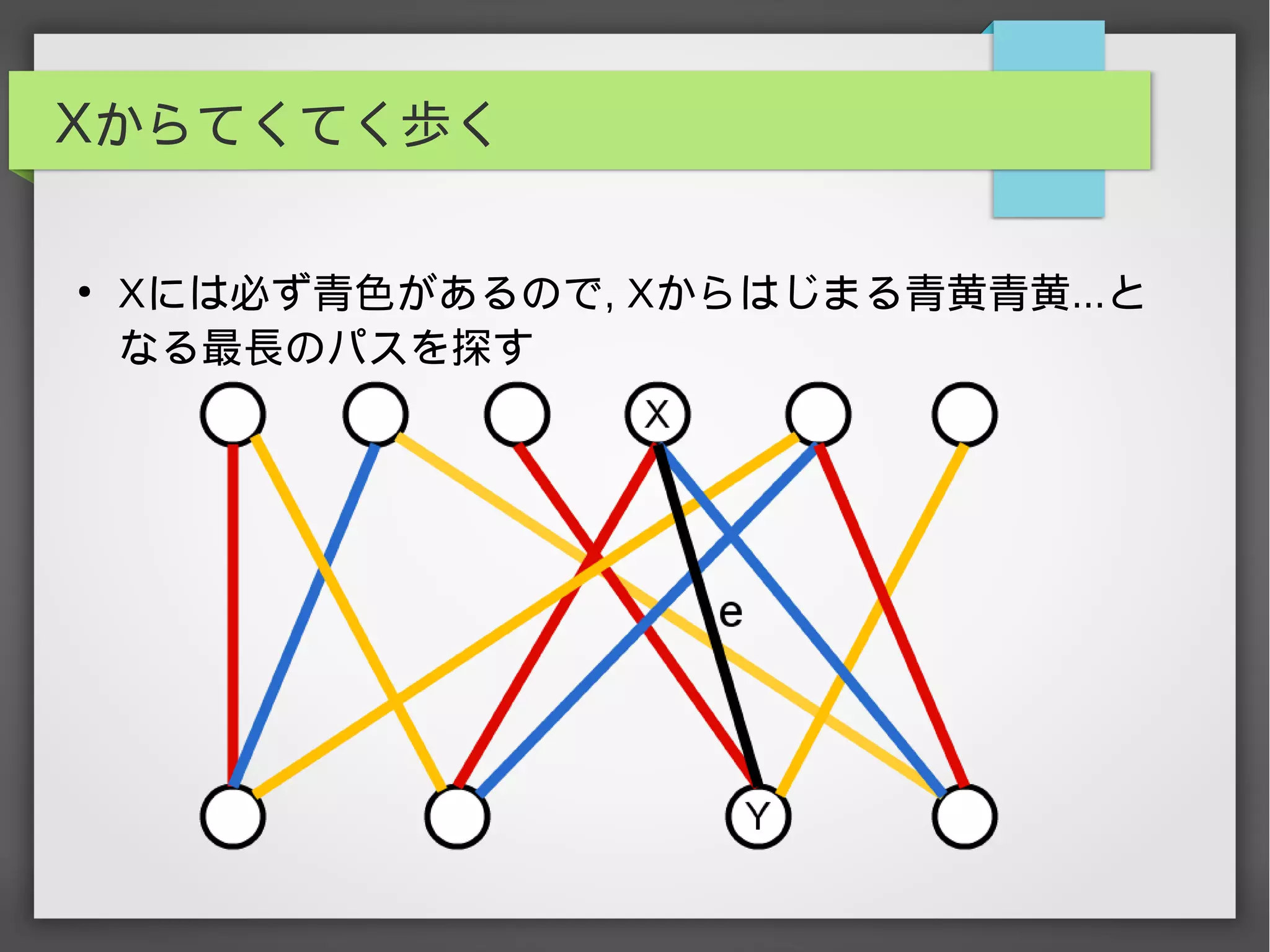
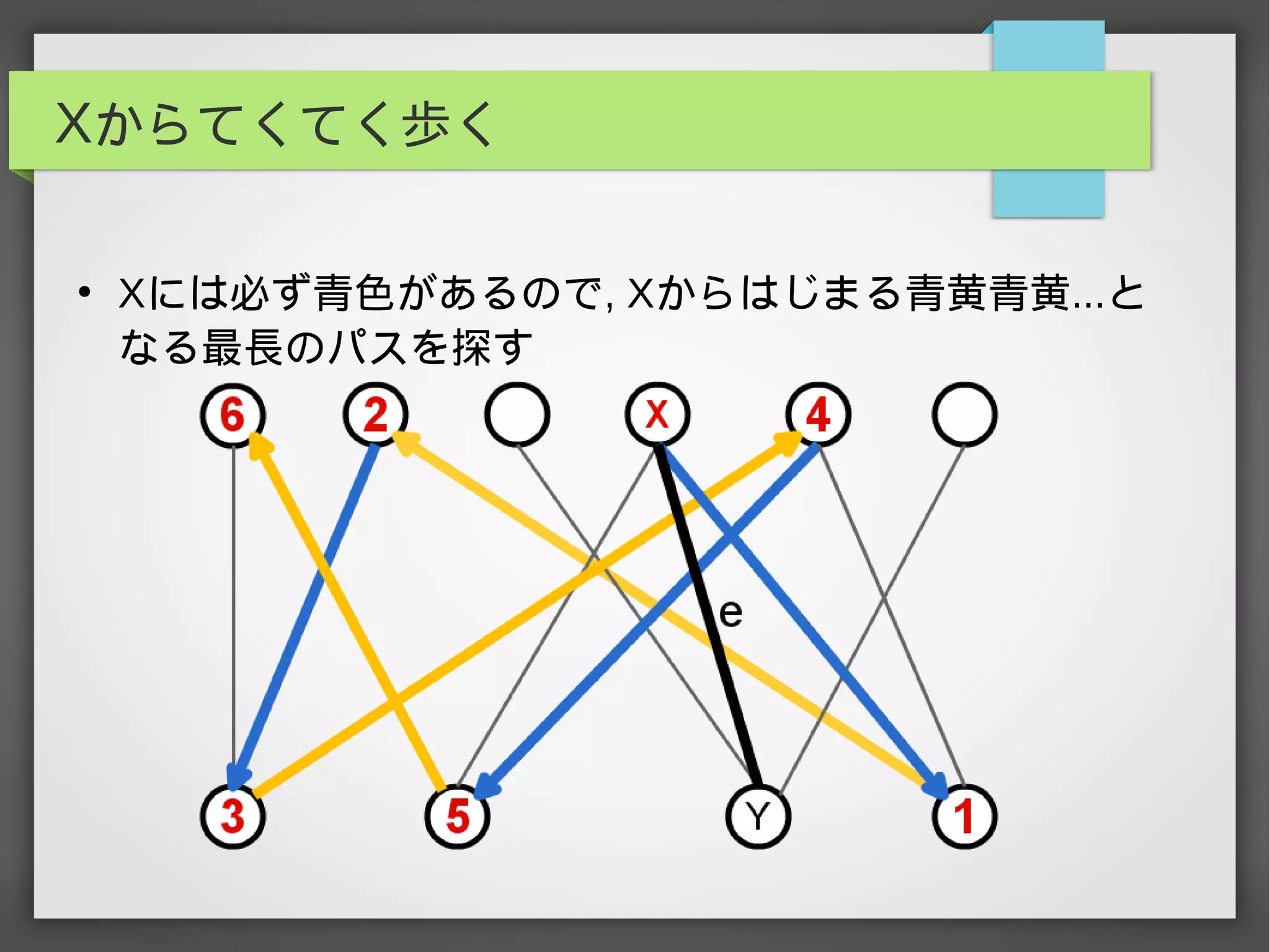
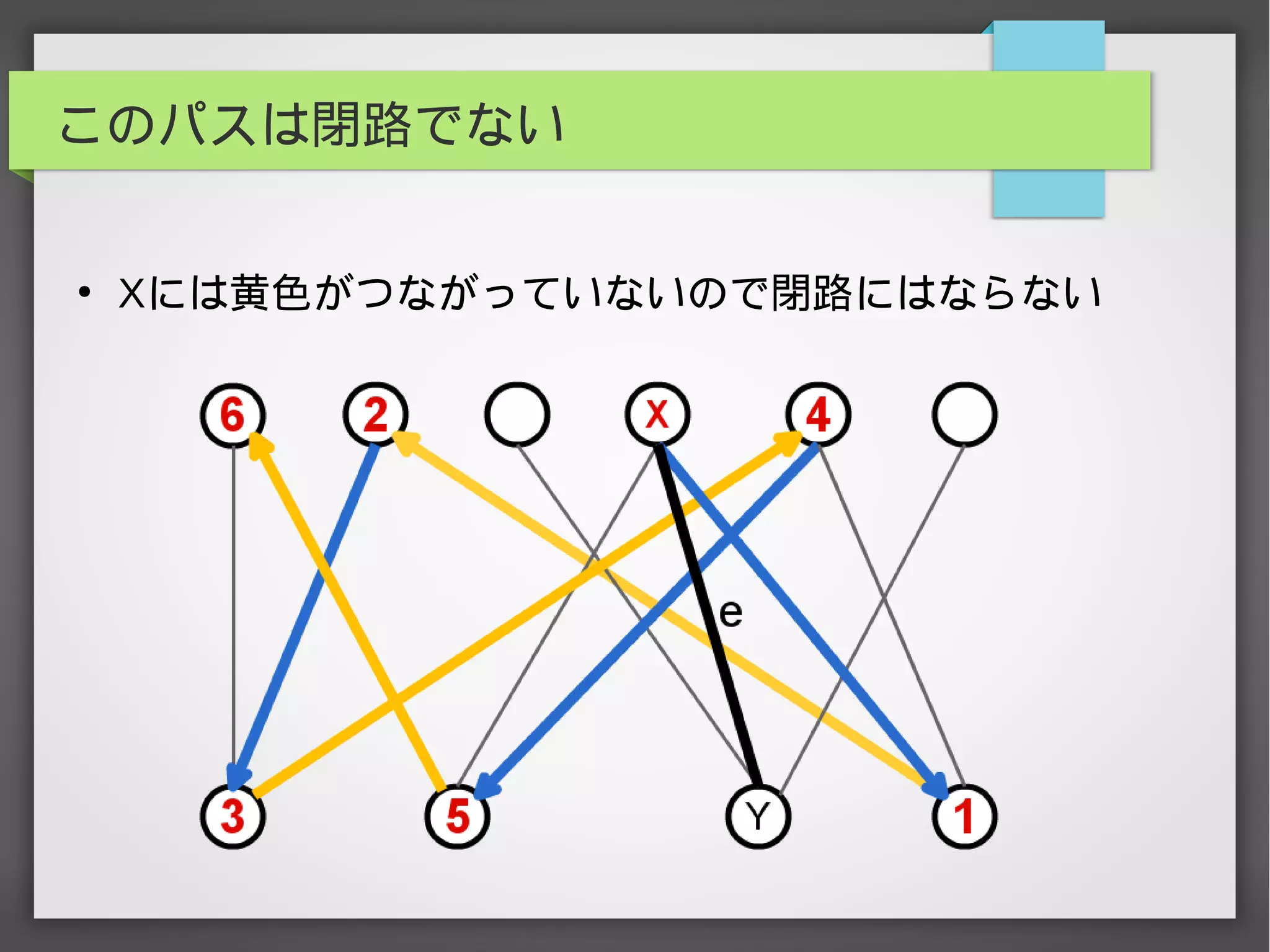
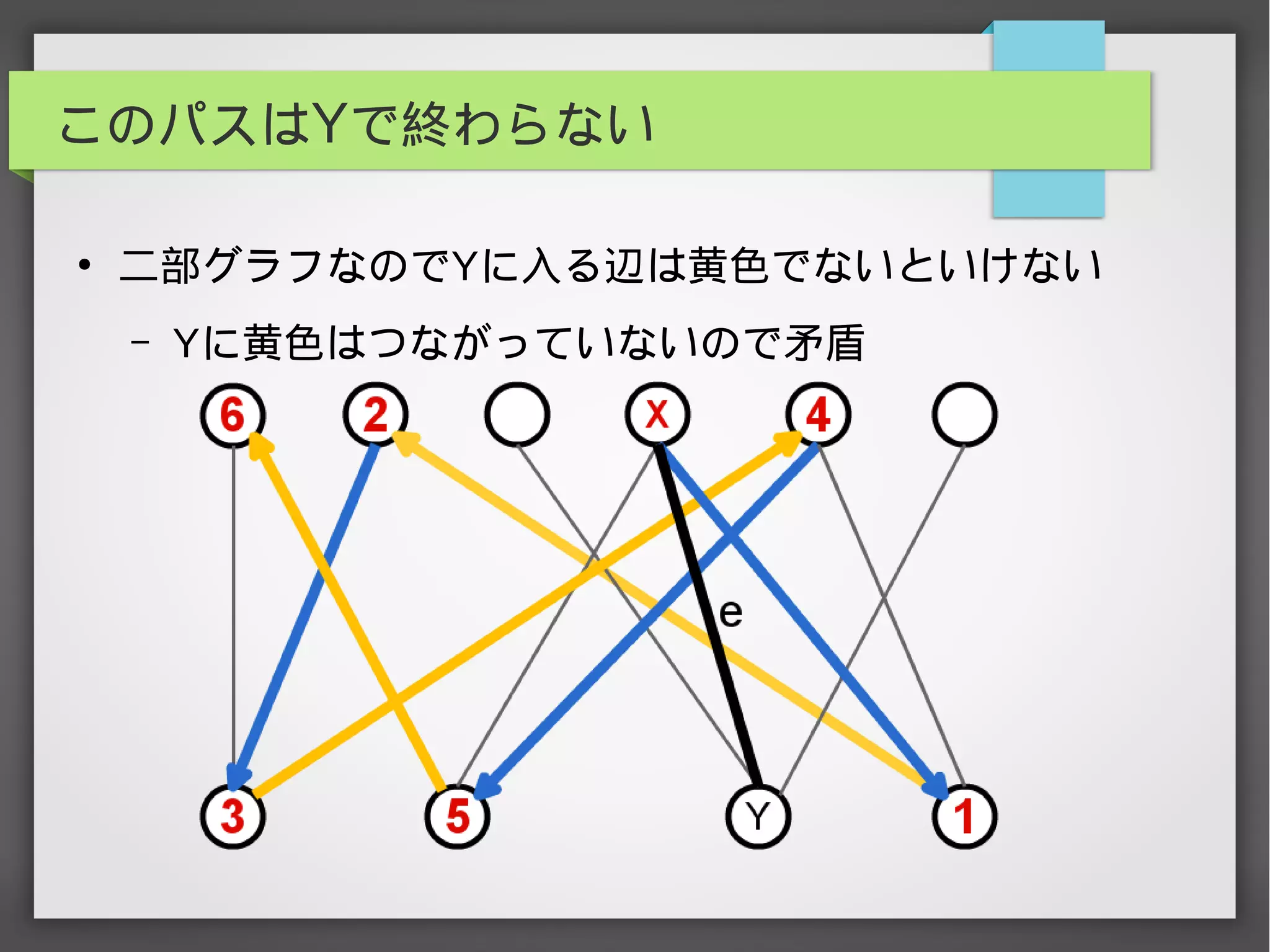
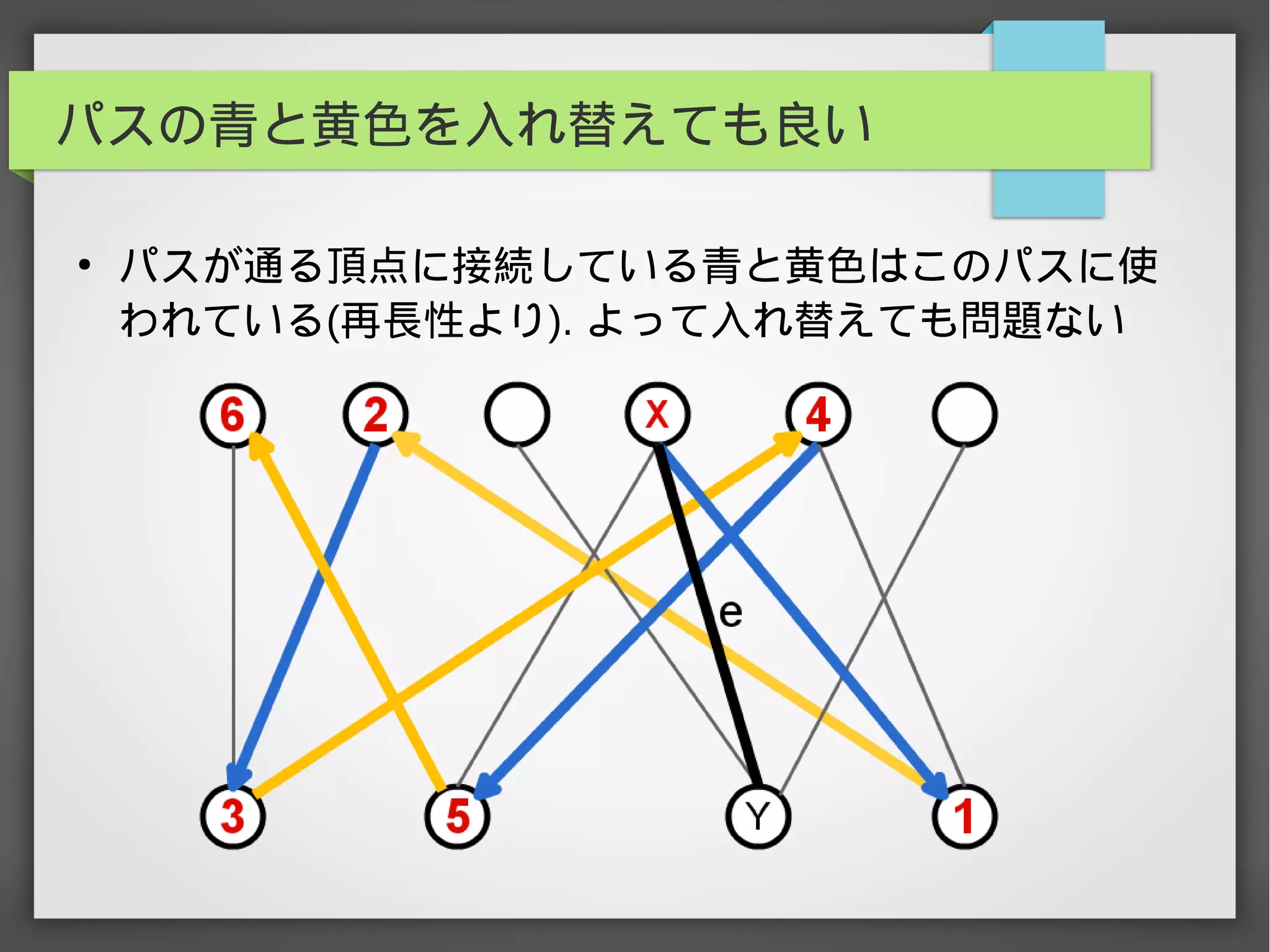
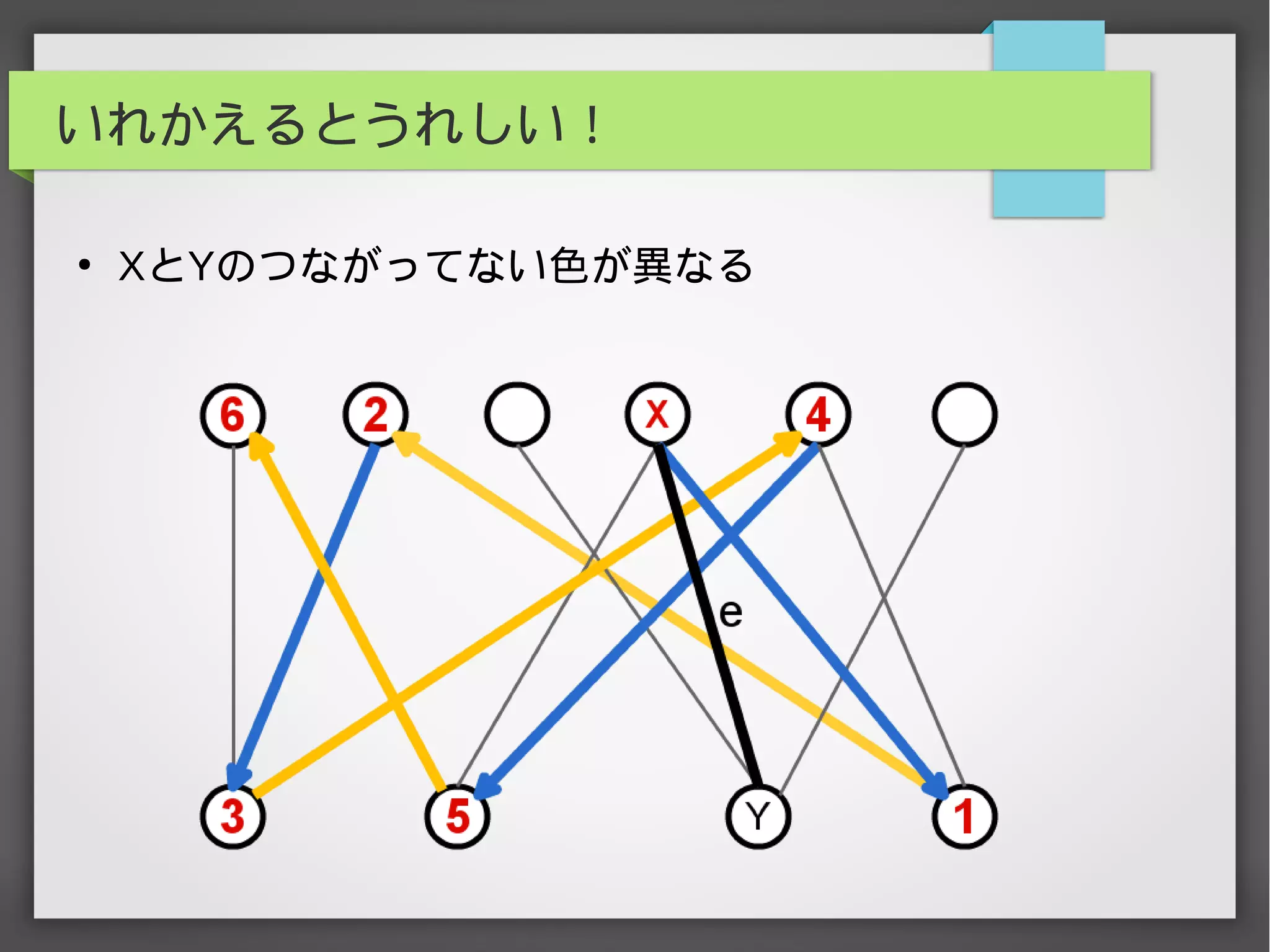
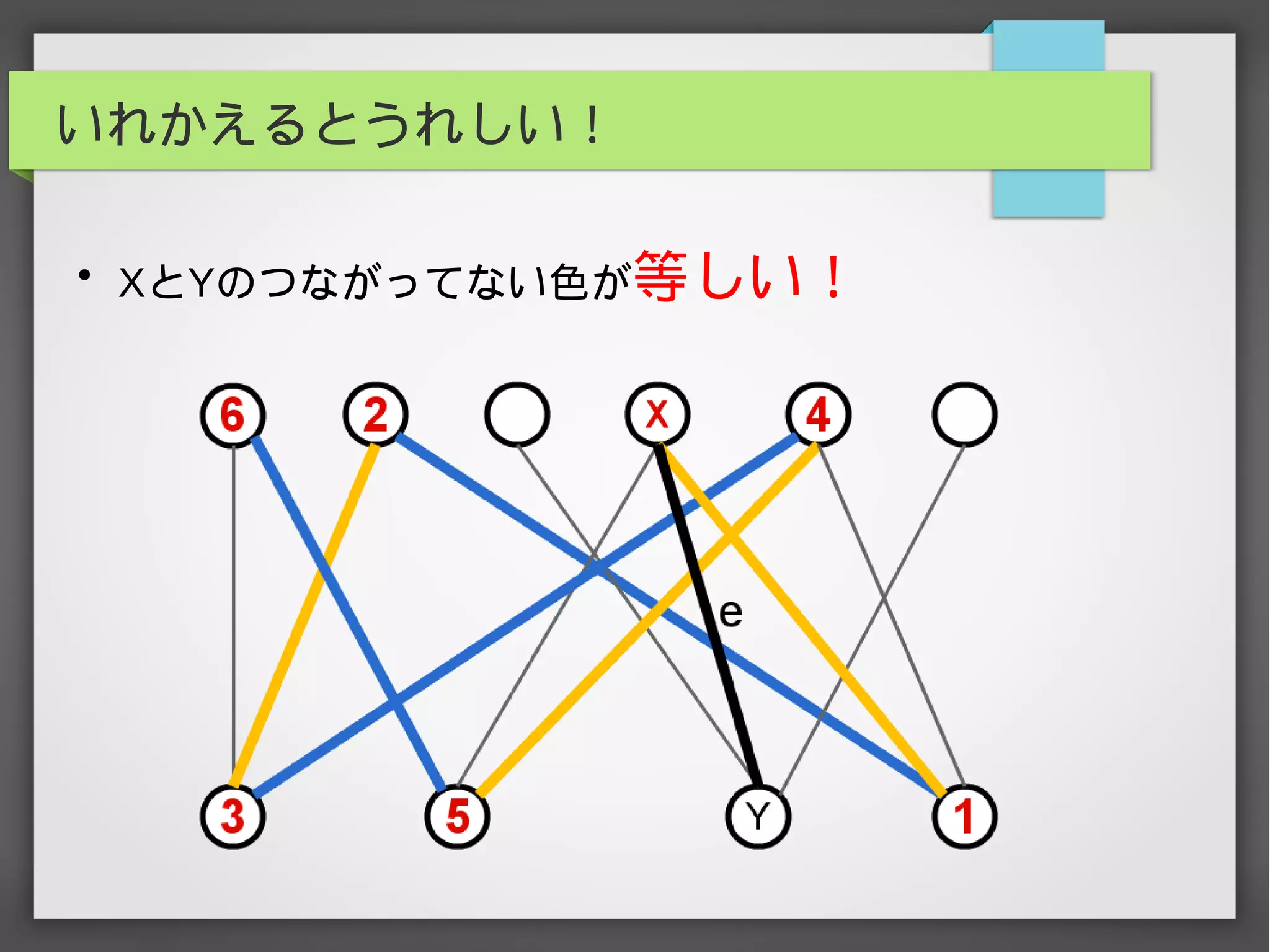
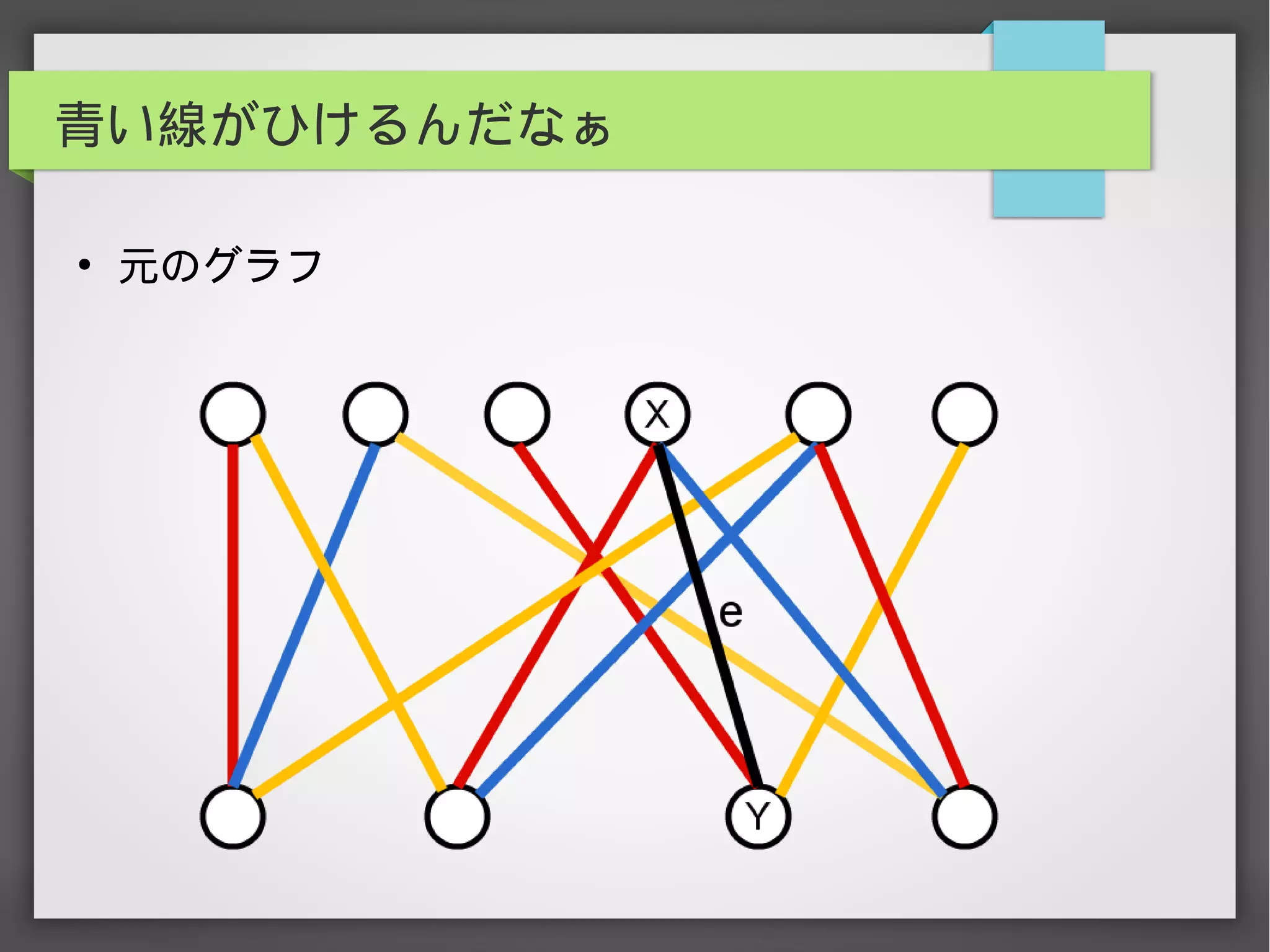
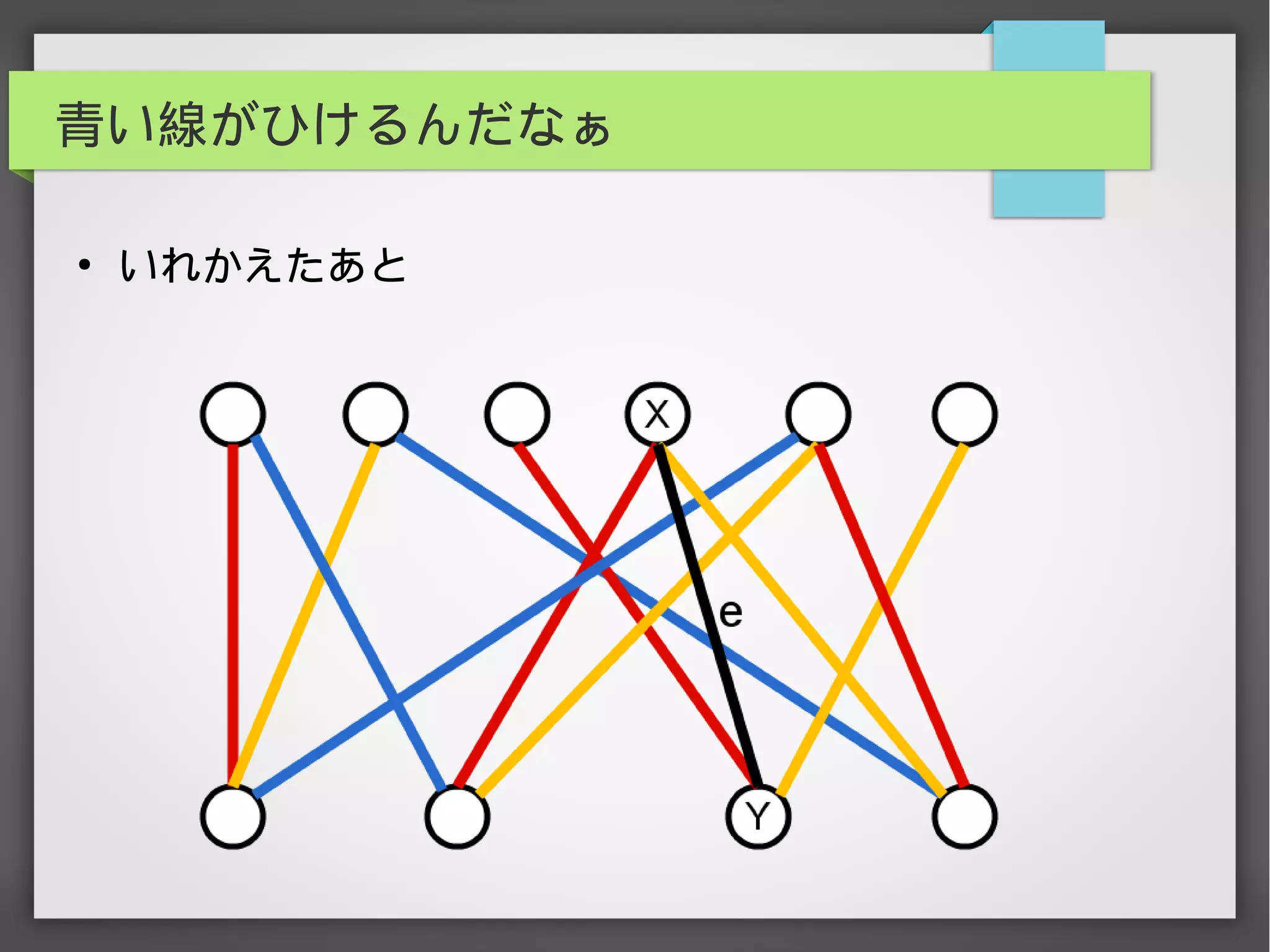
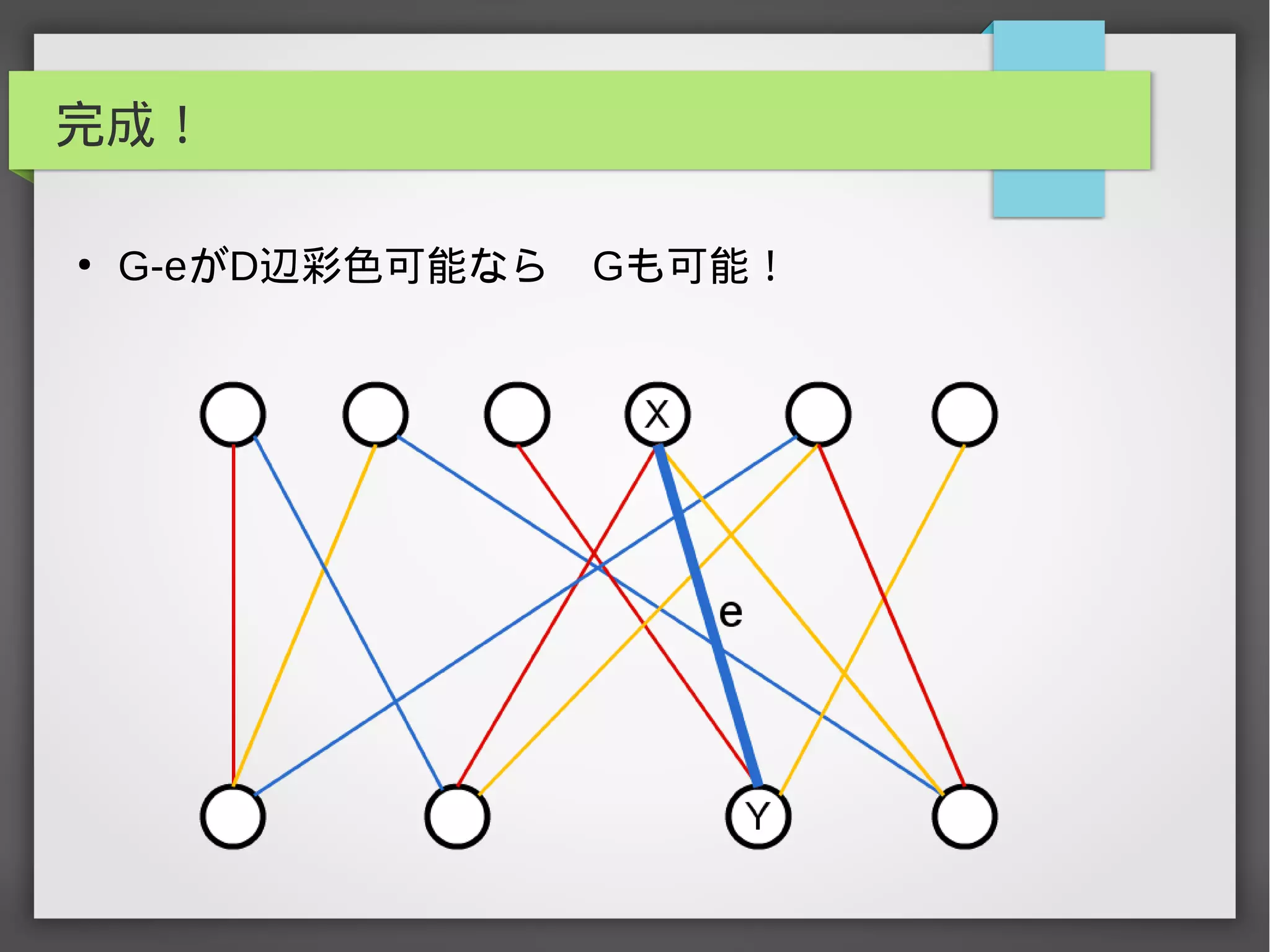
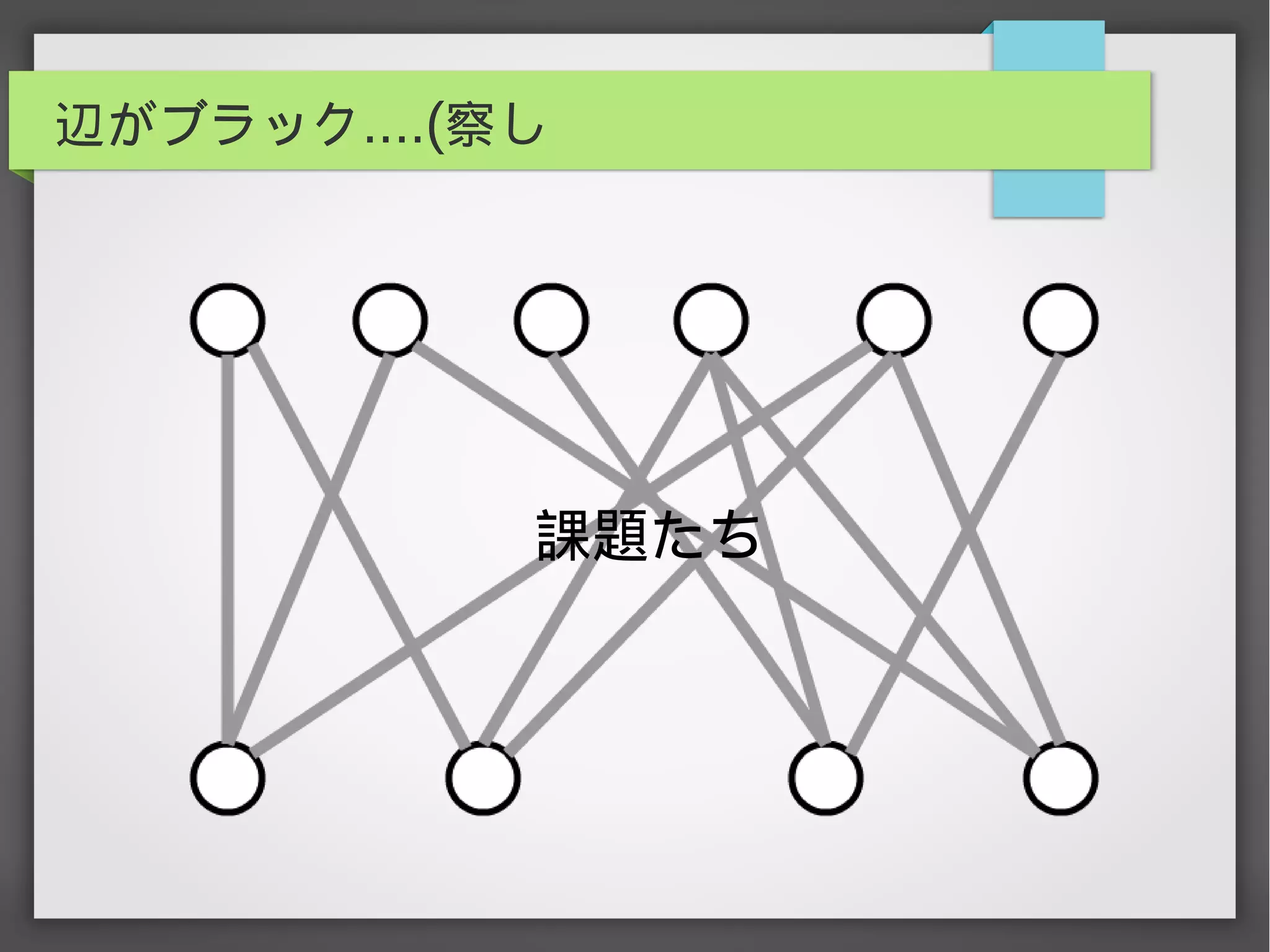
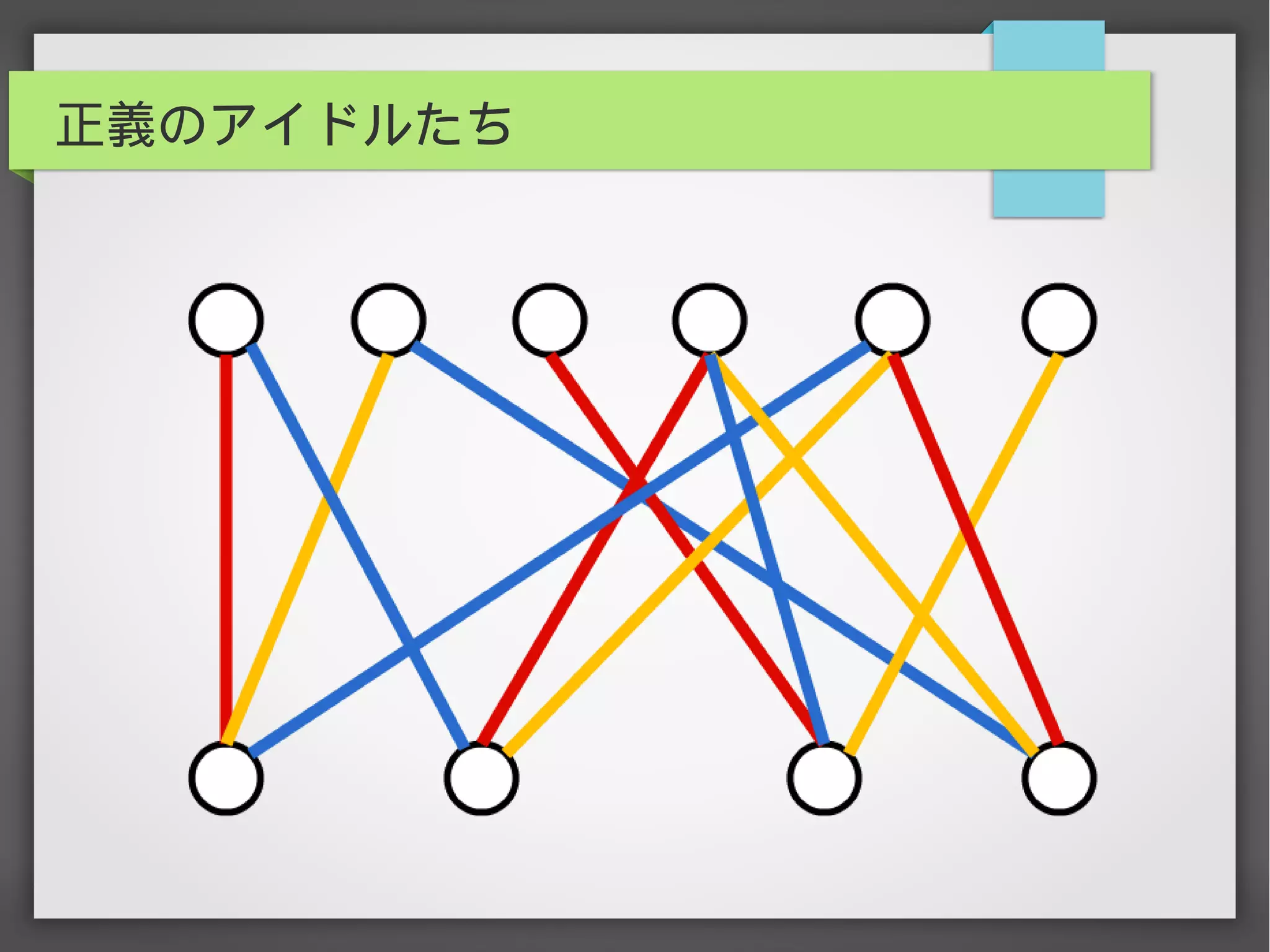
辺彩色
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.