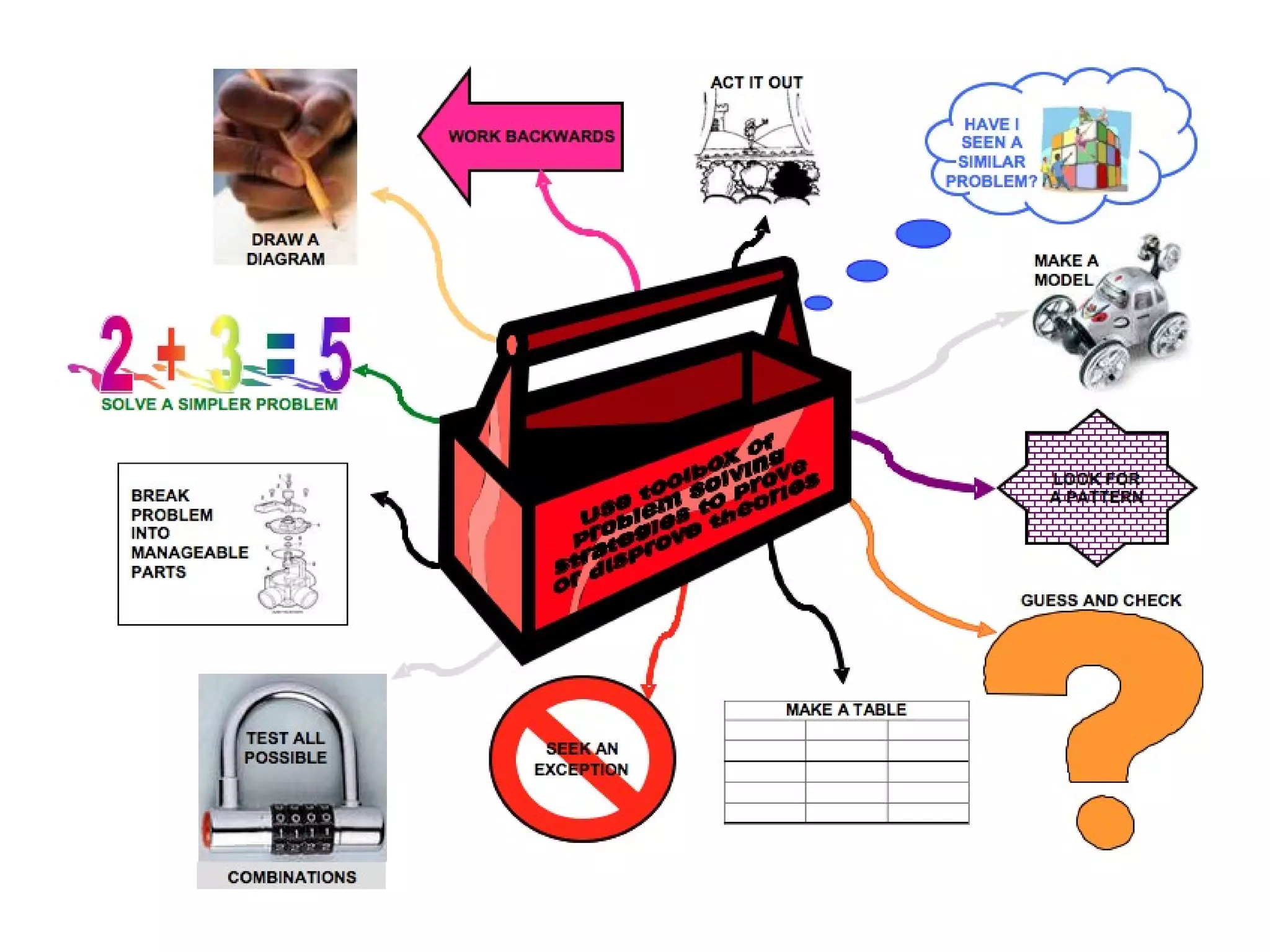
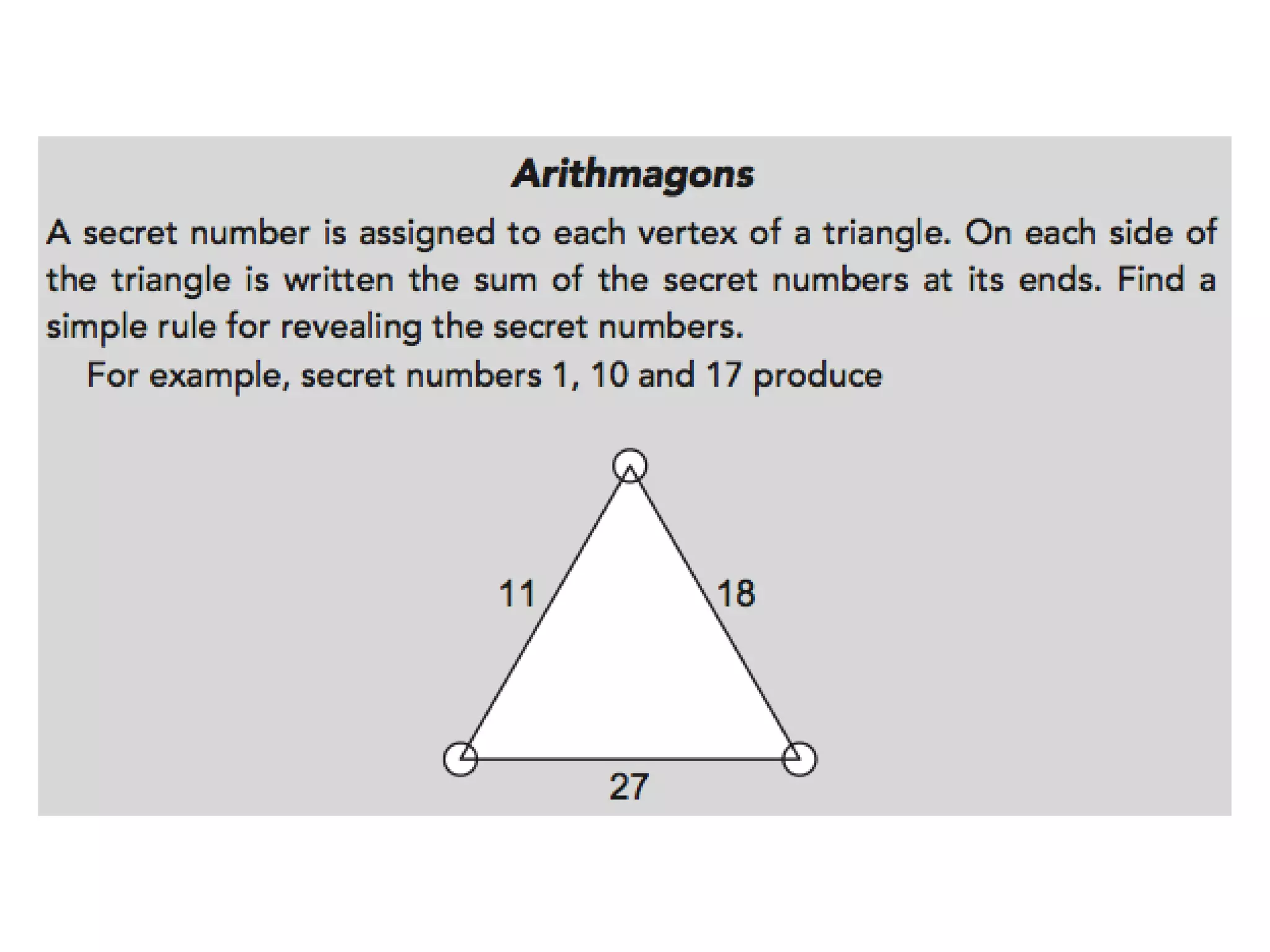
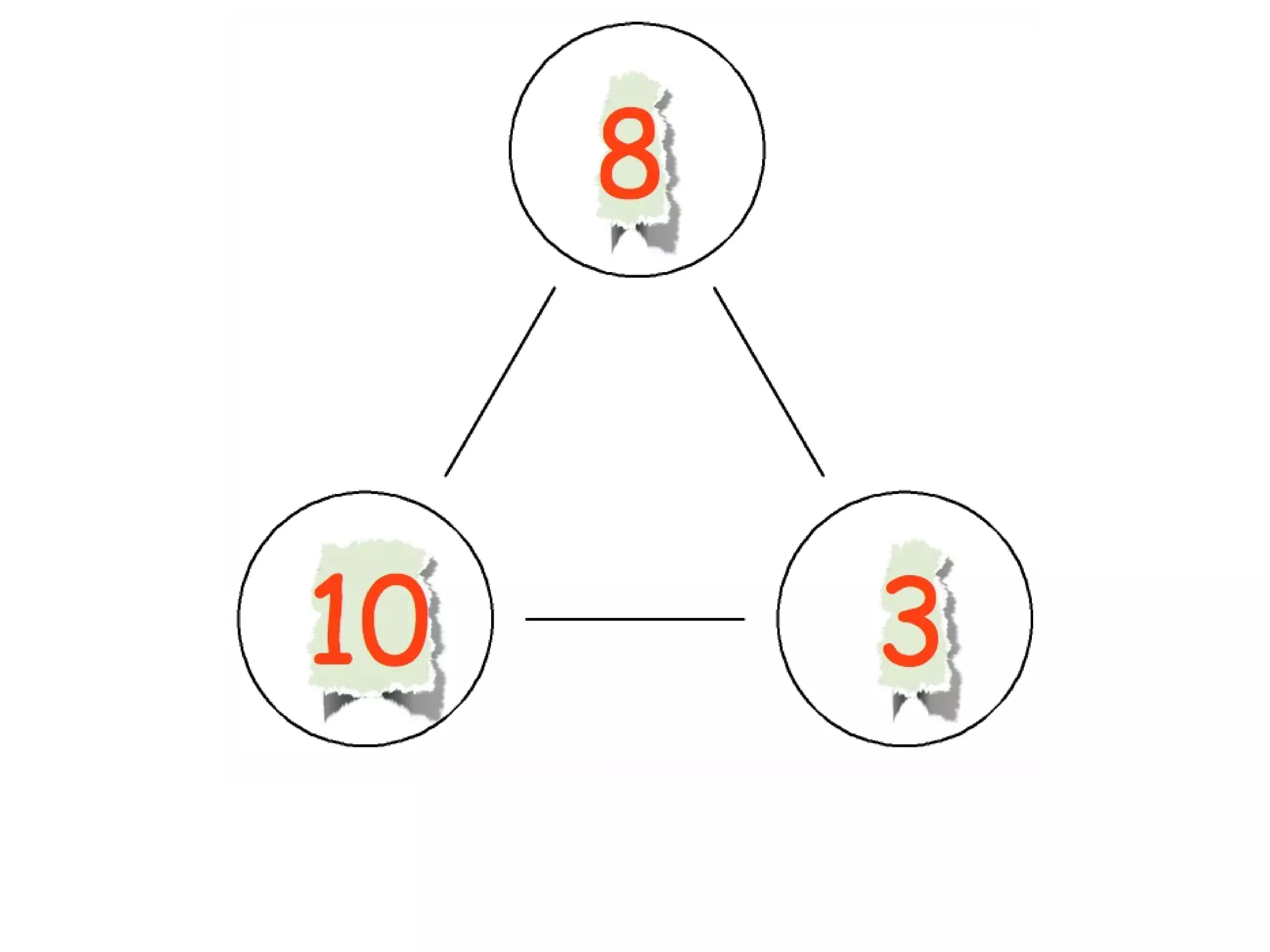
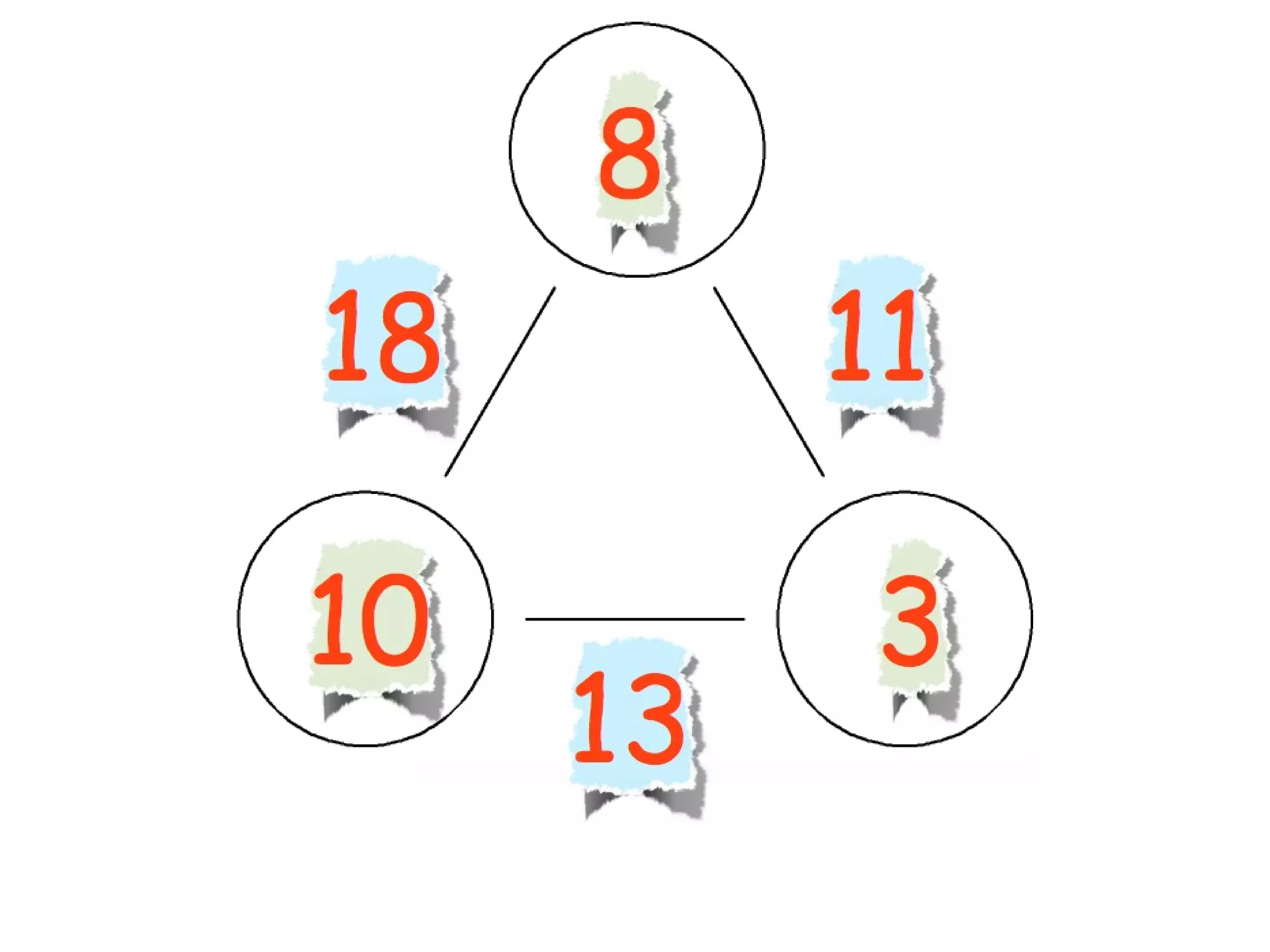
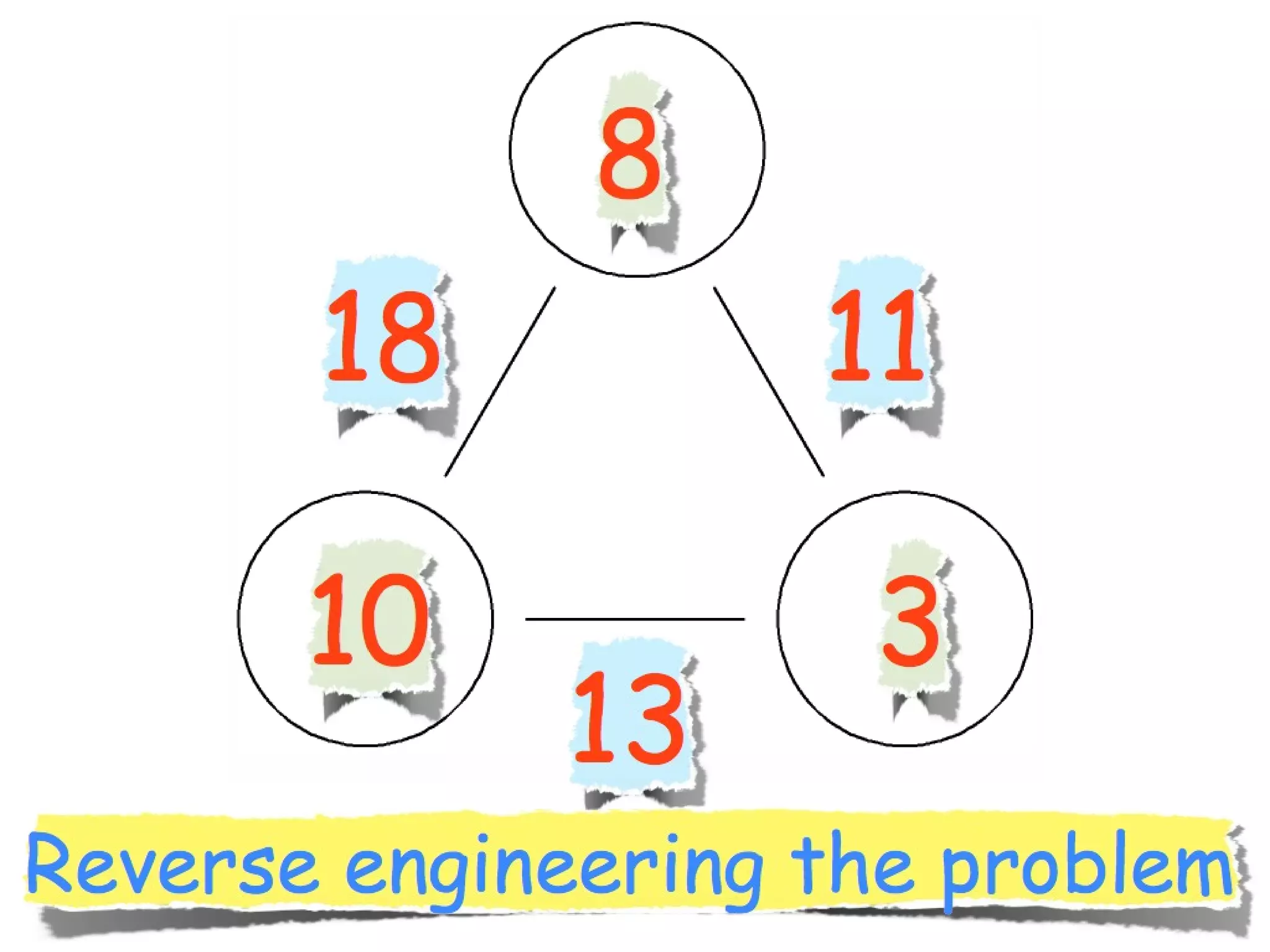
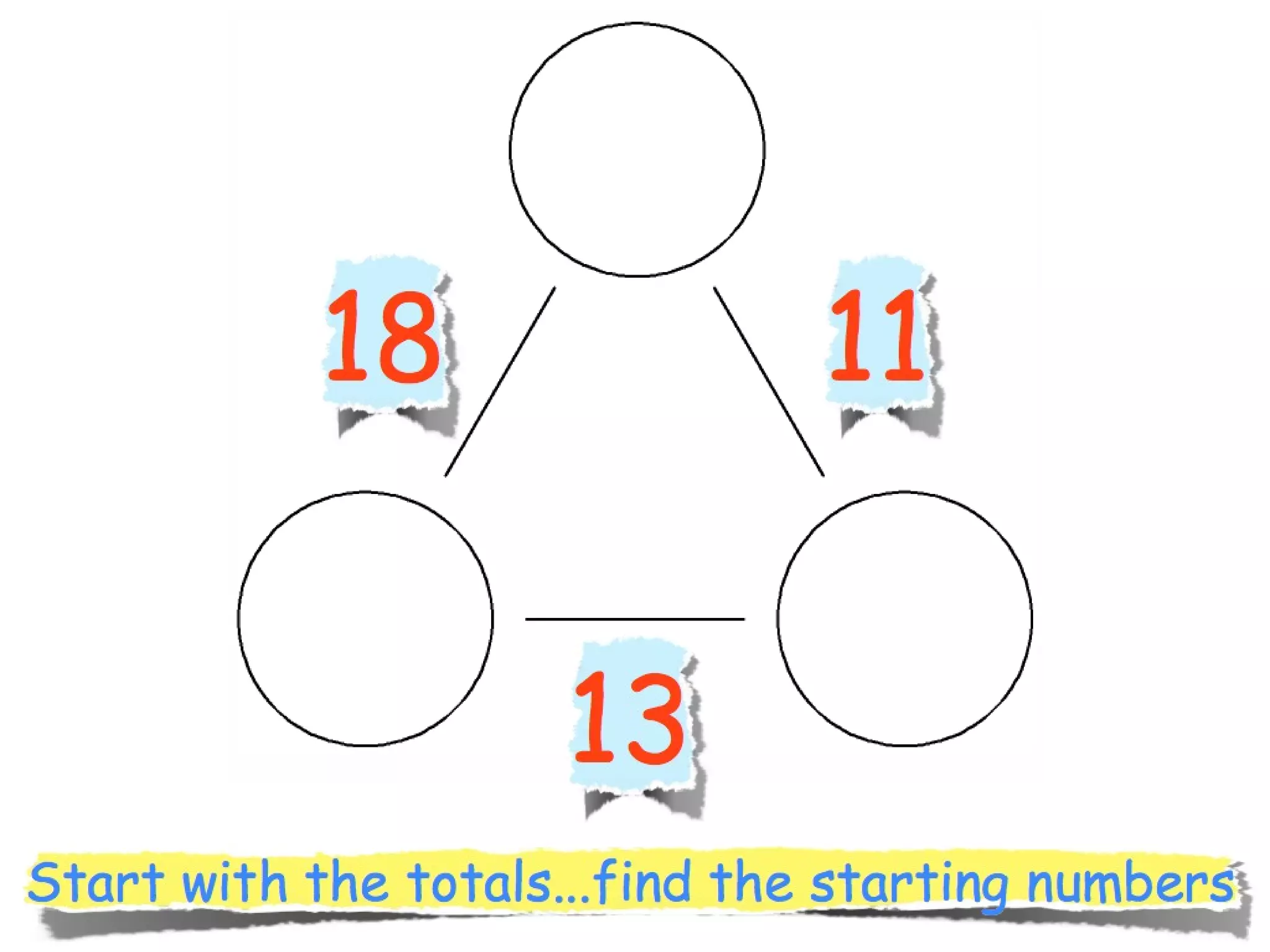
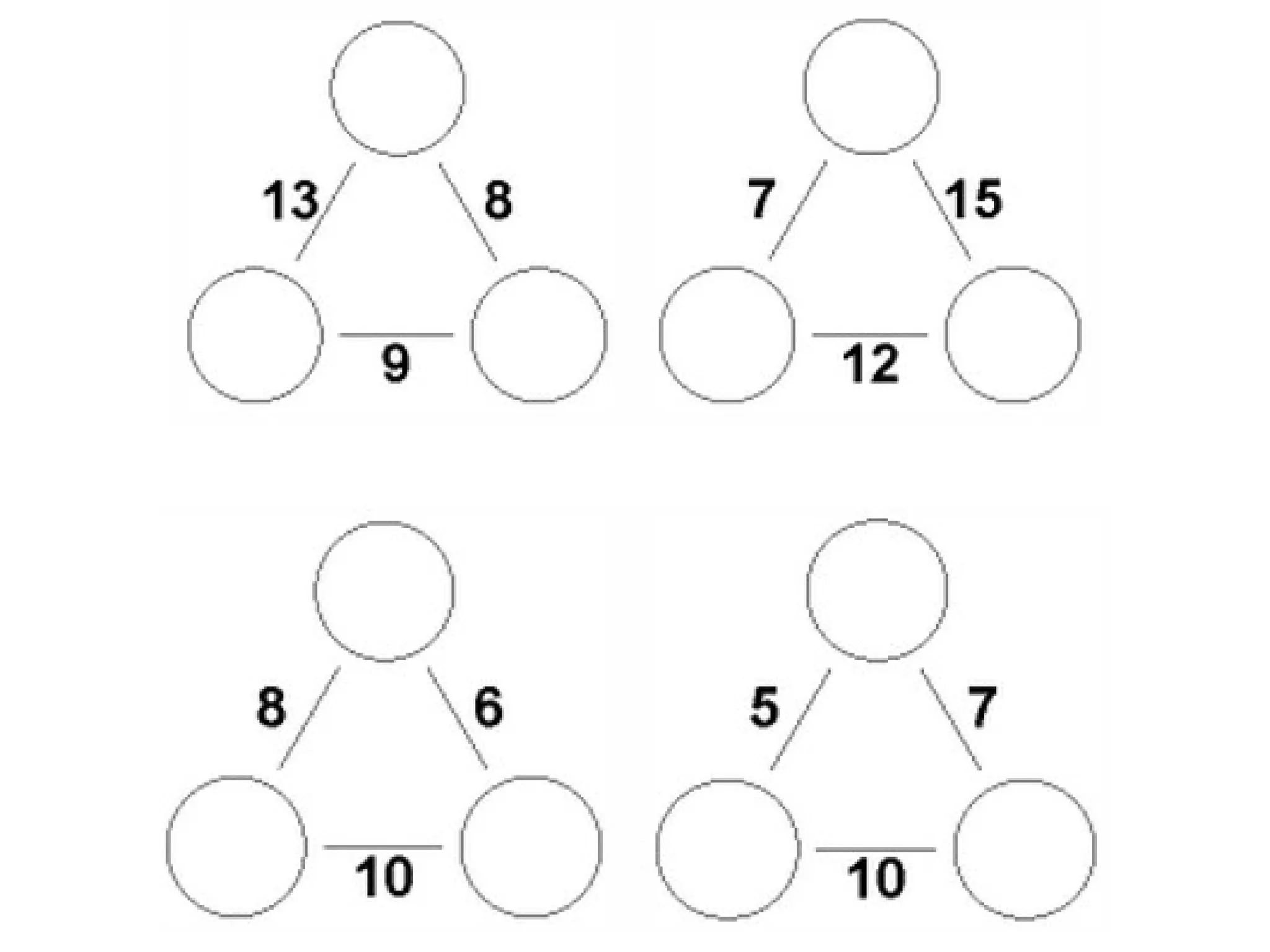
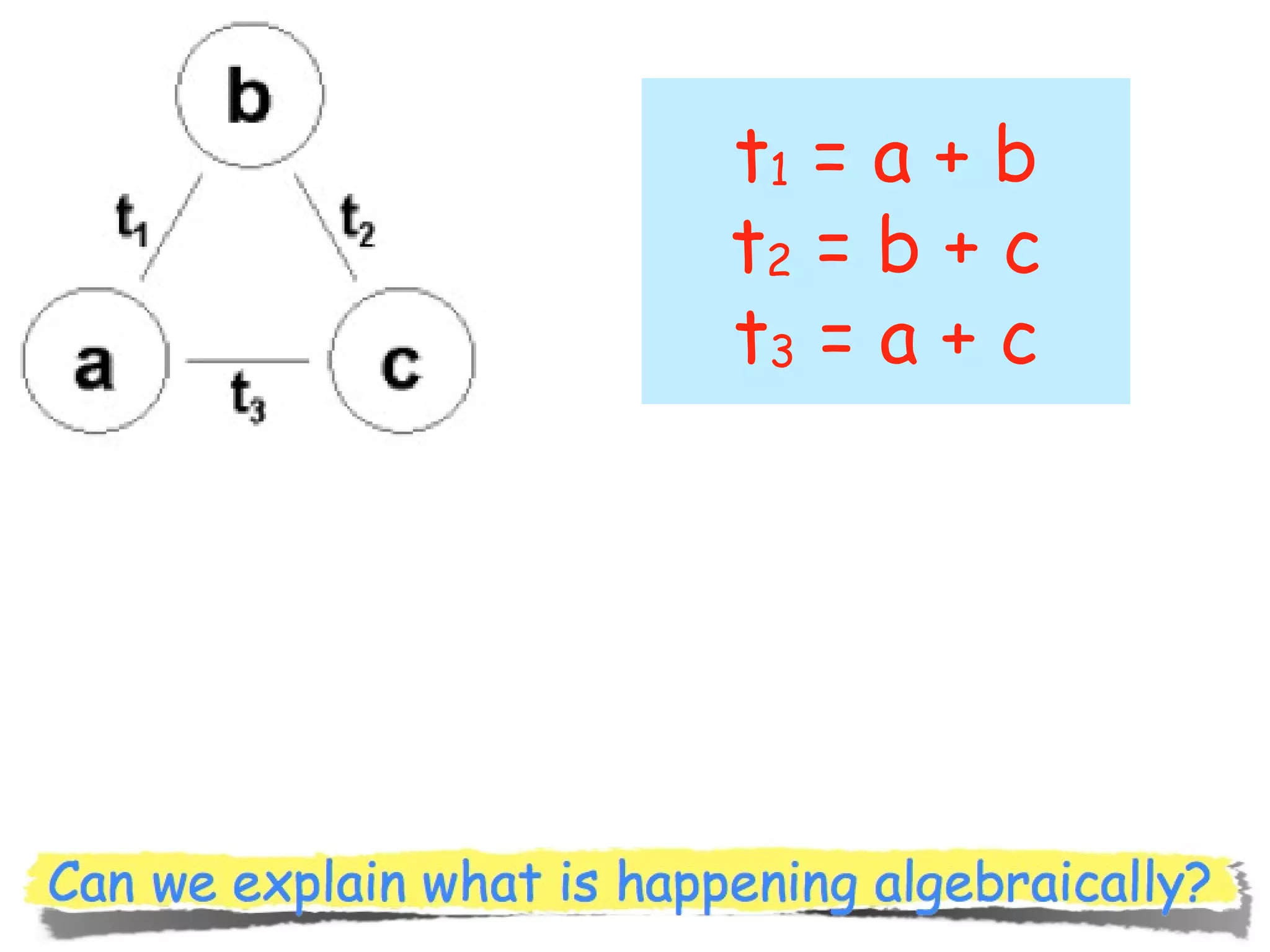
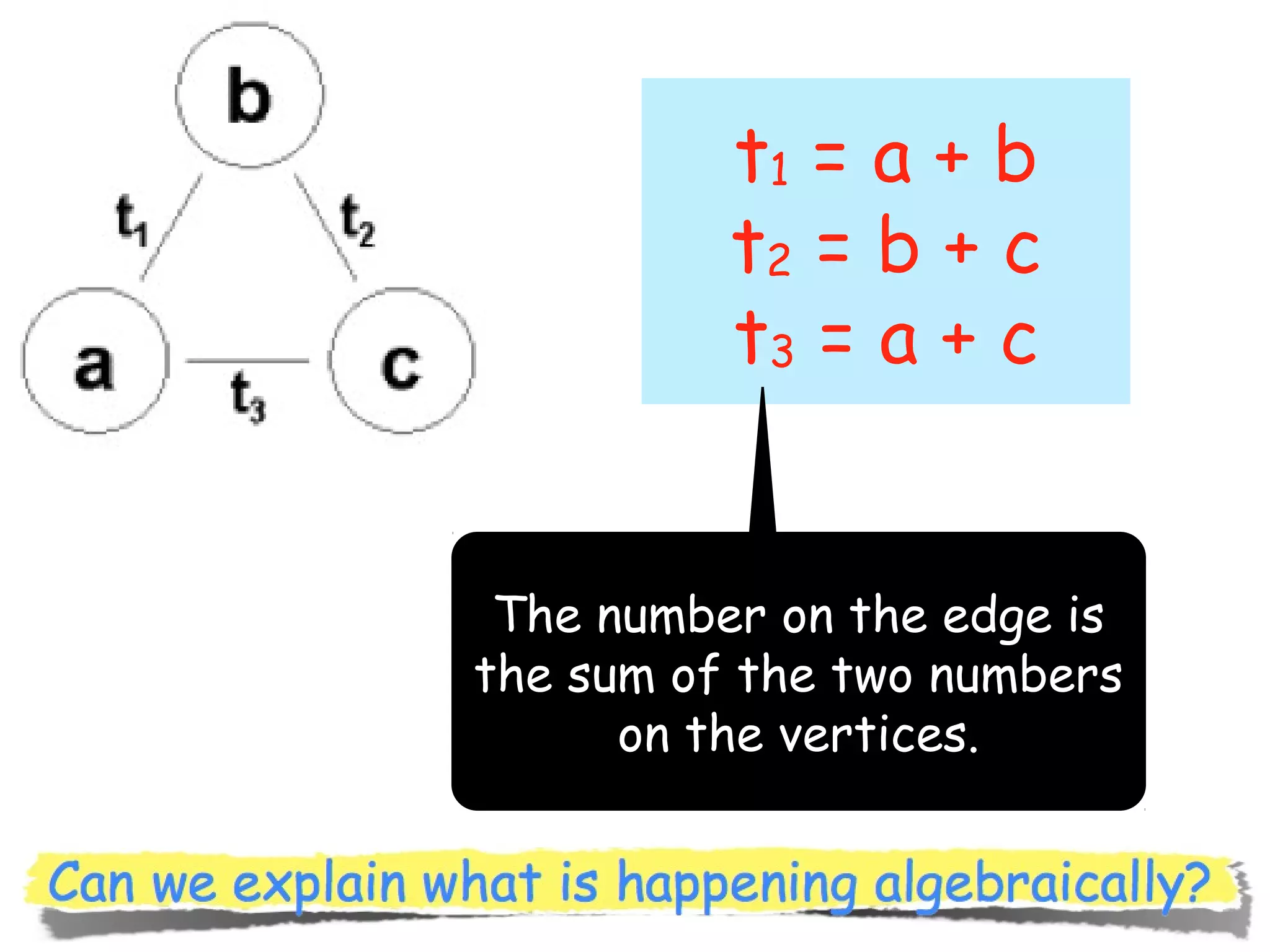
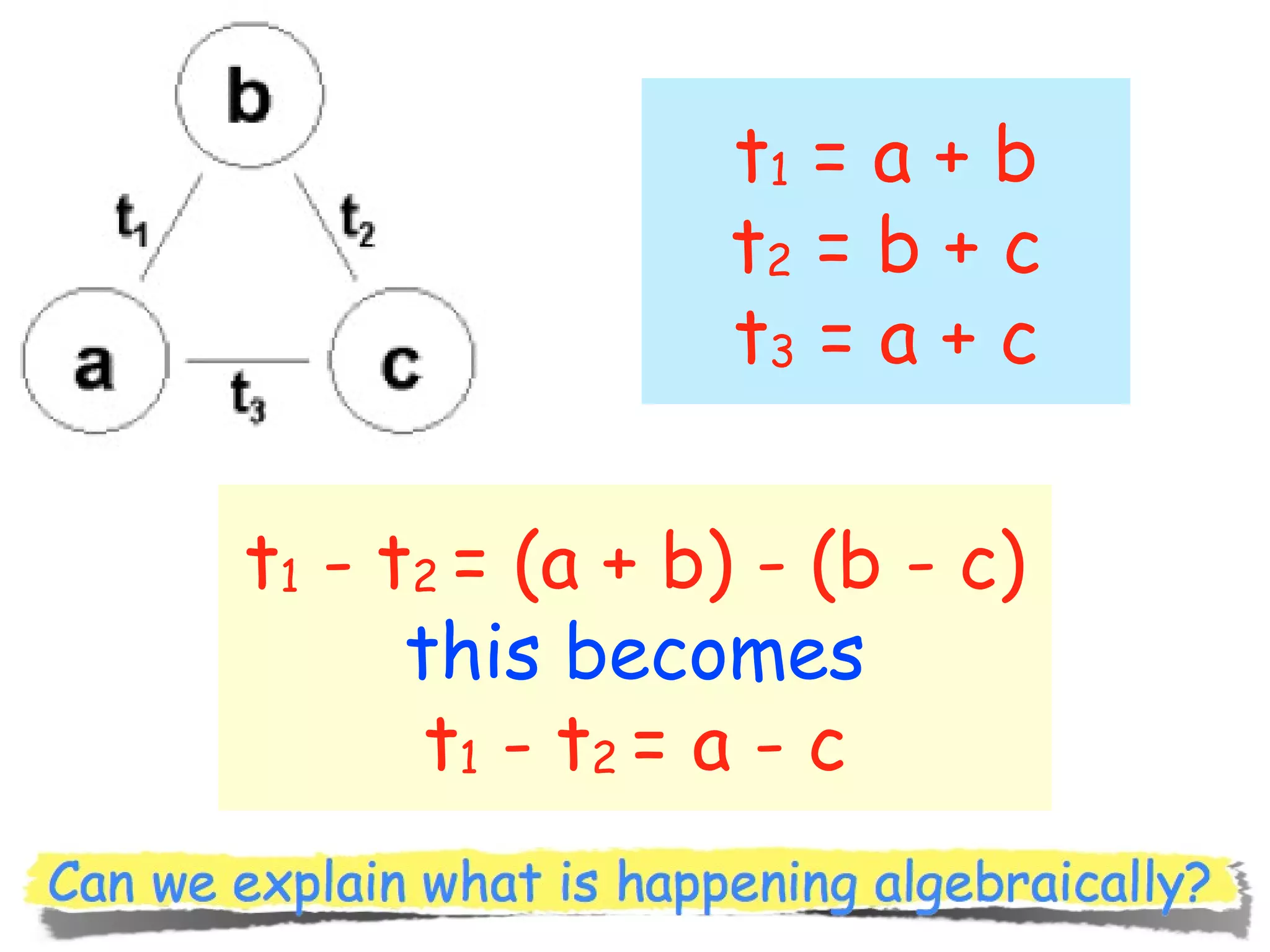
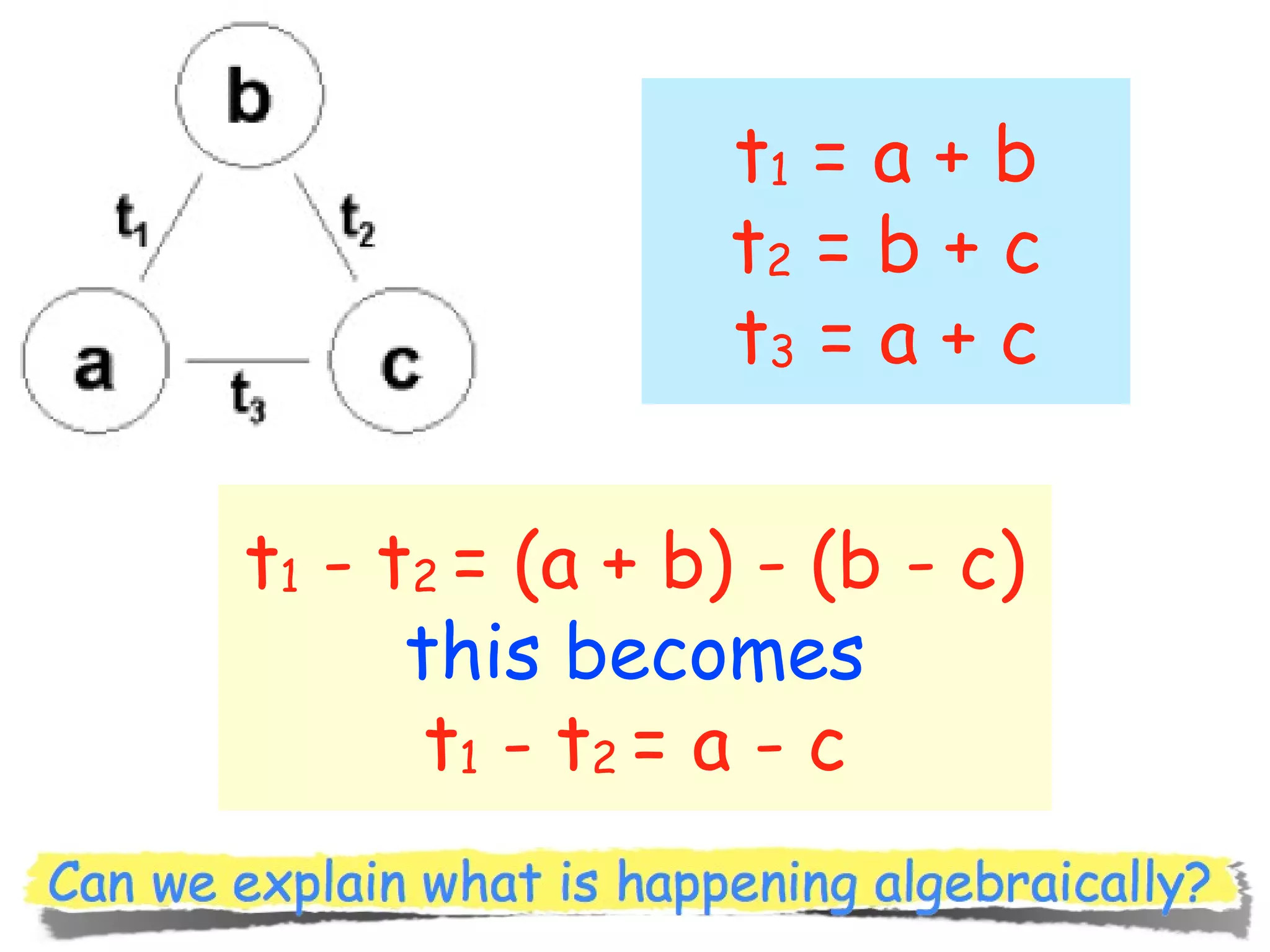
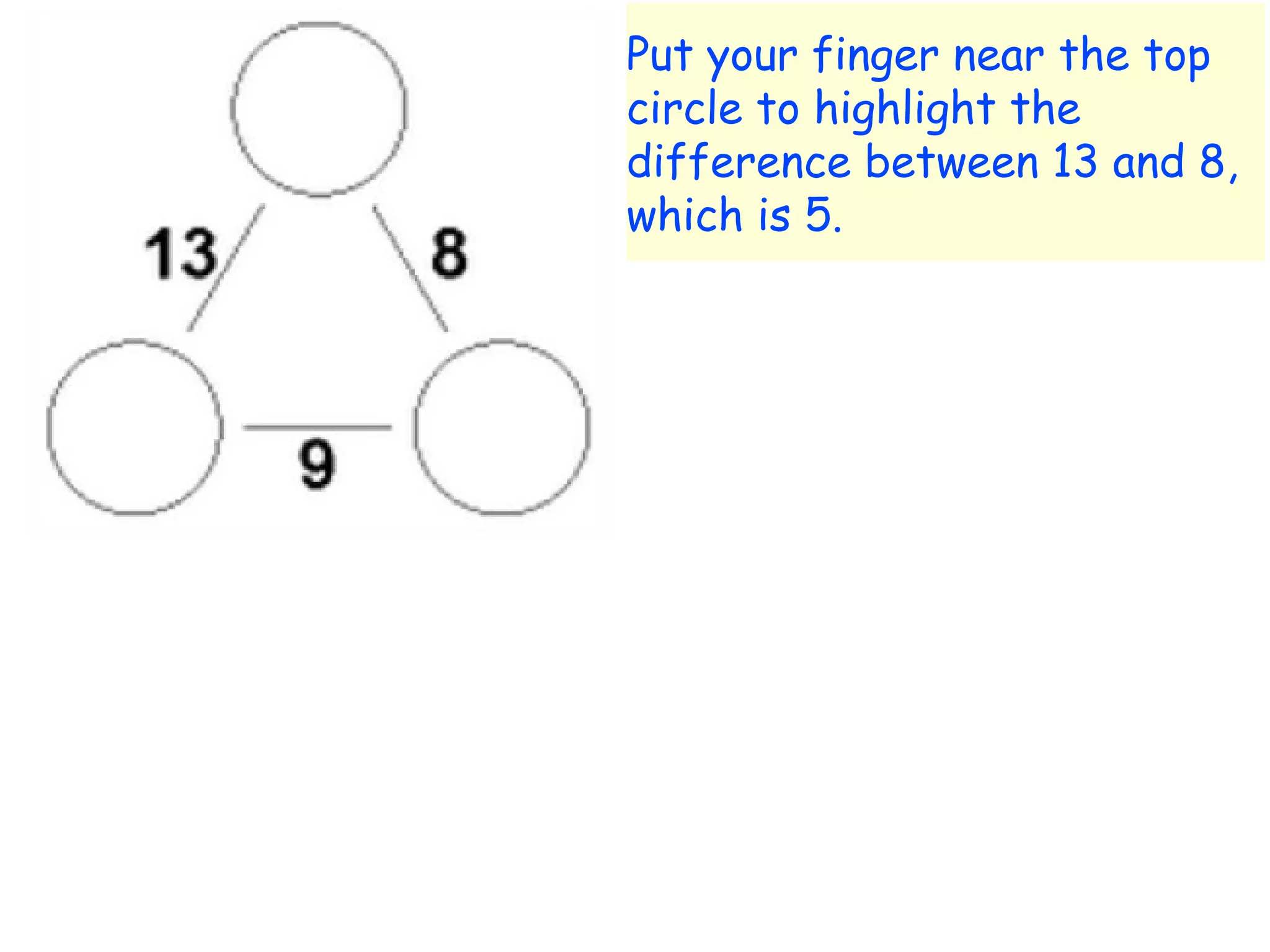
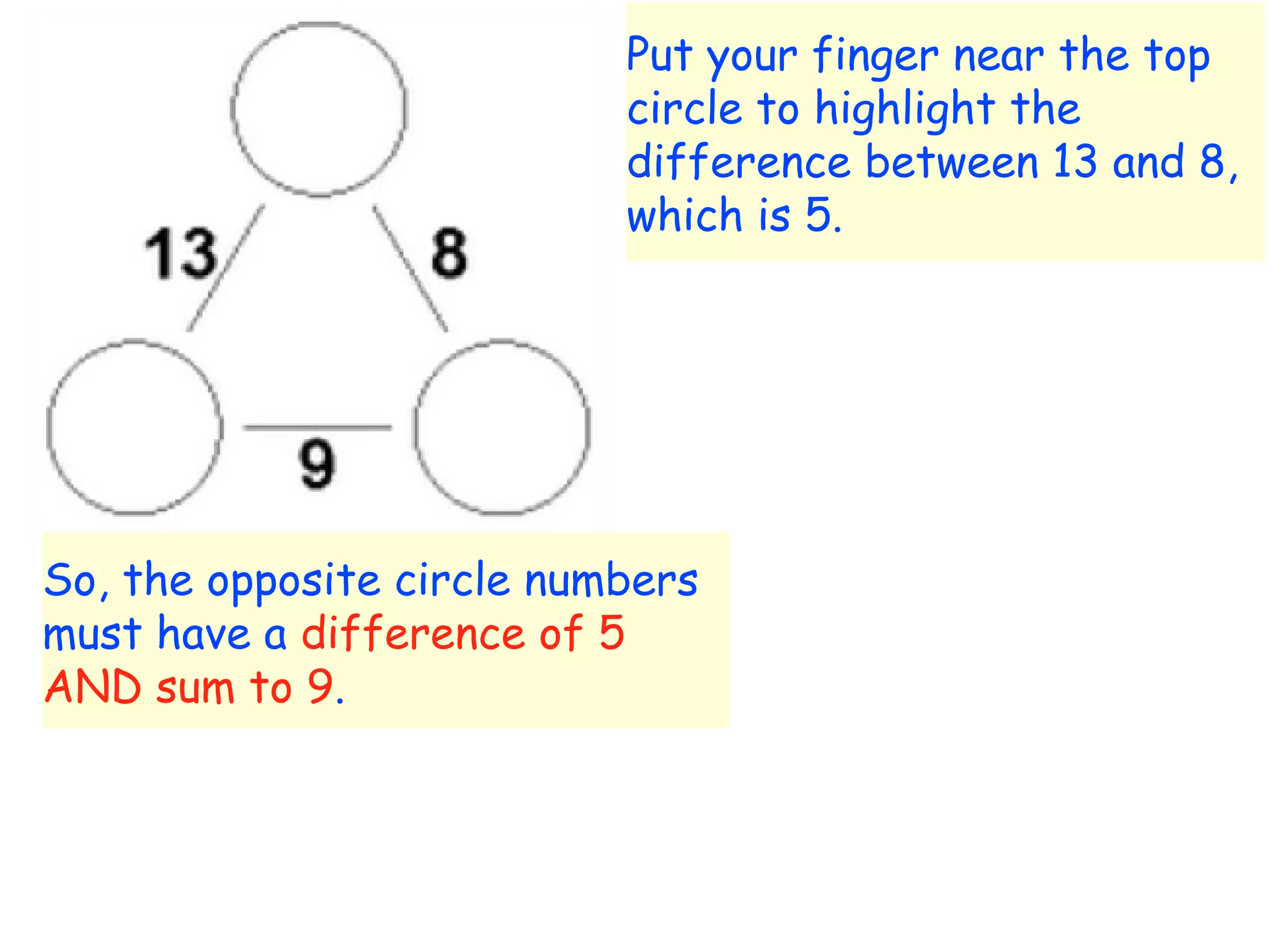
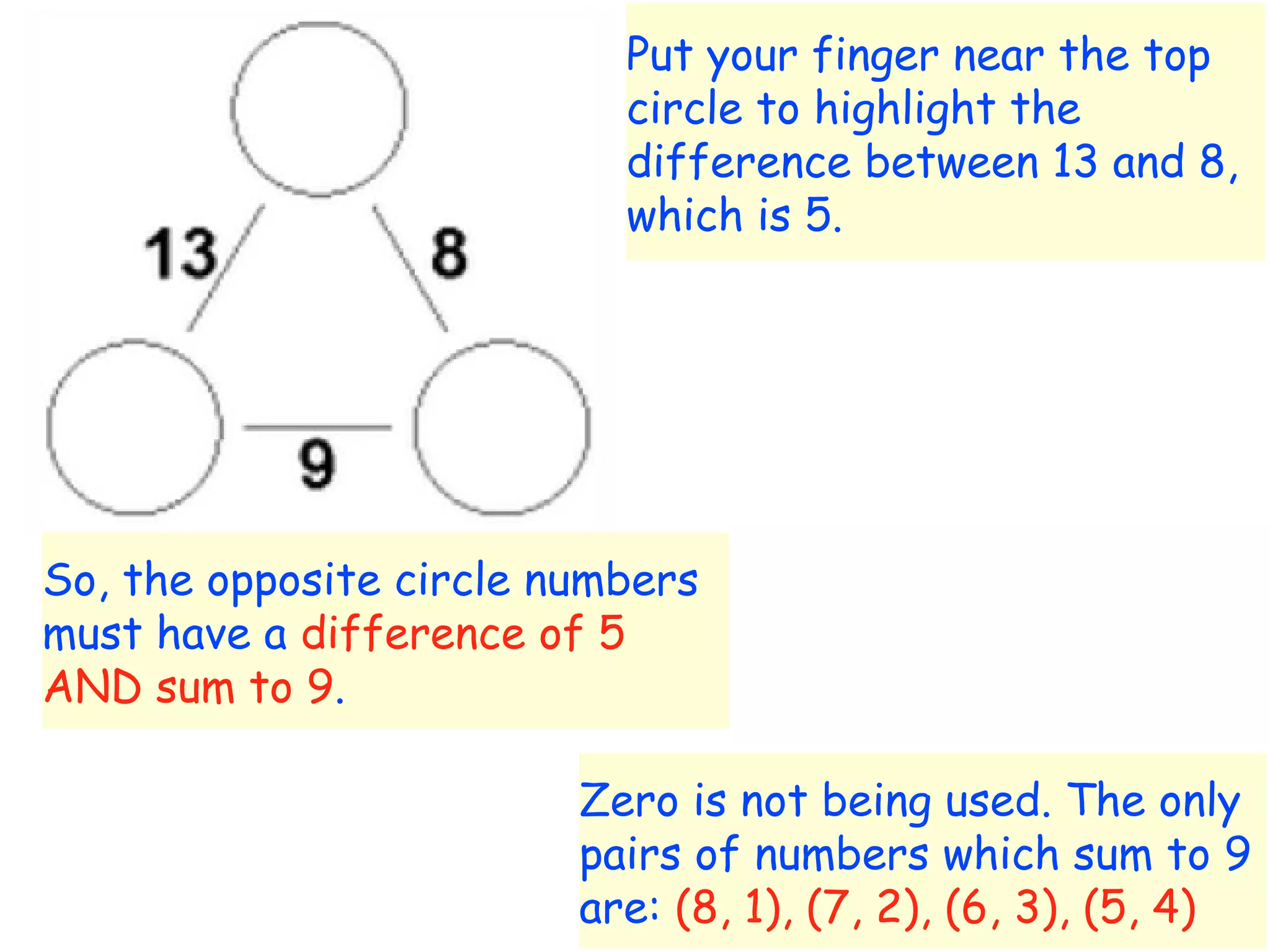
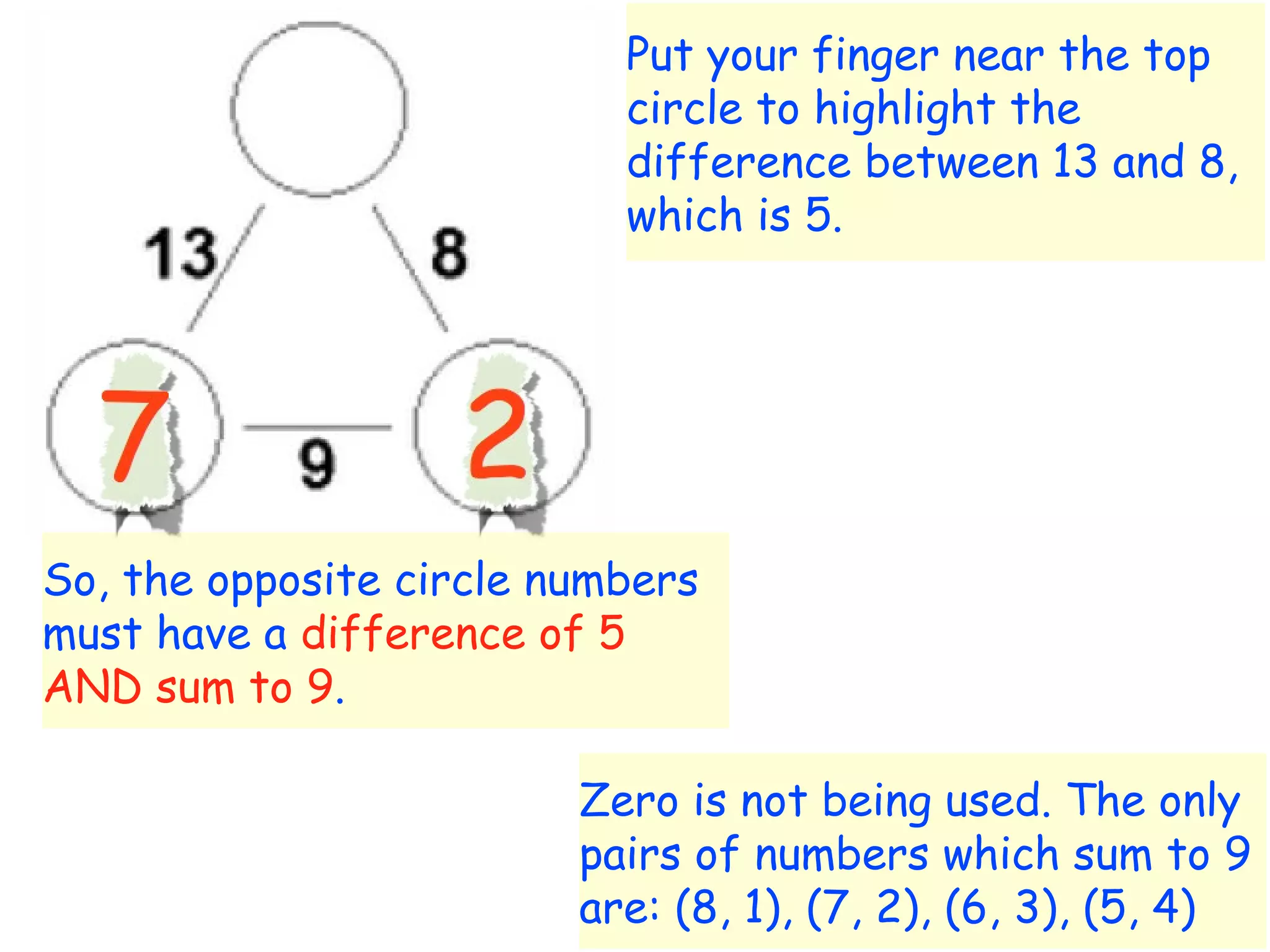
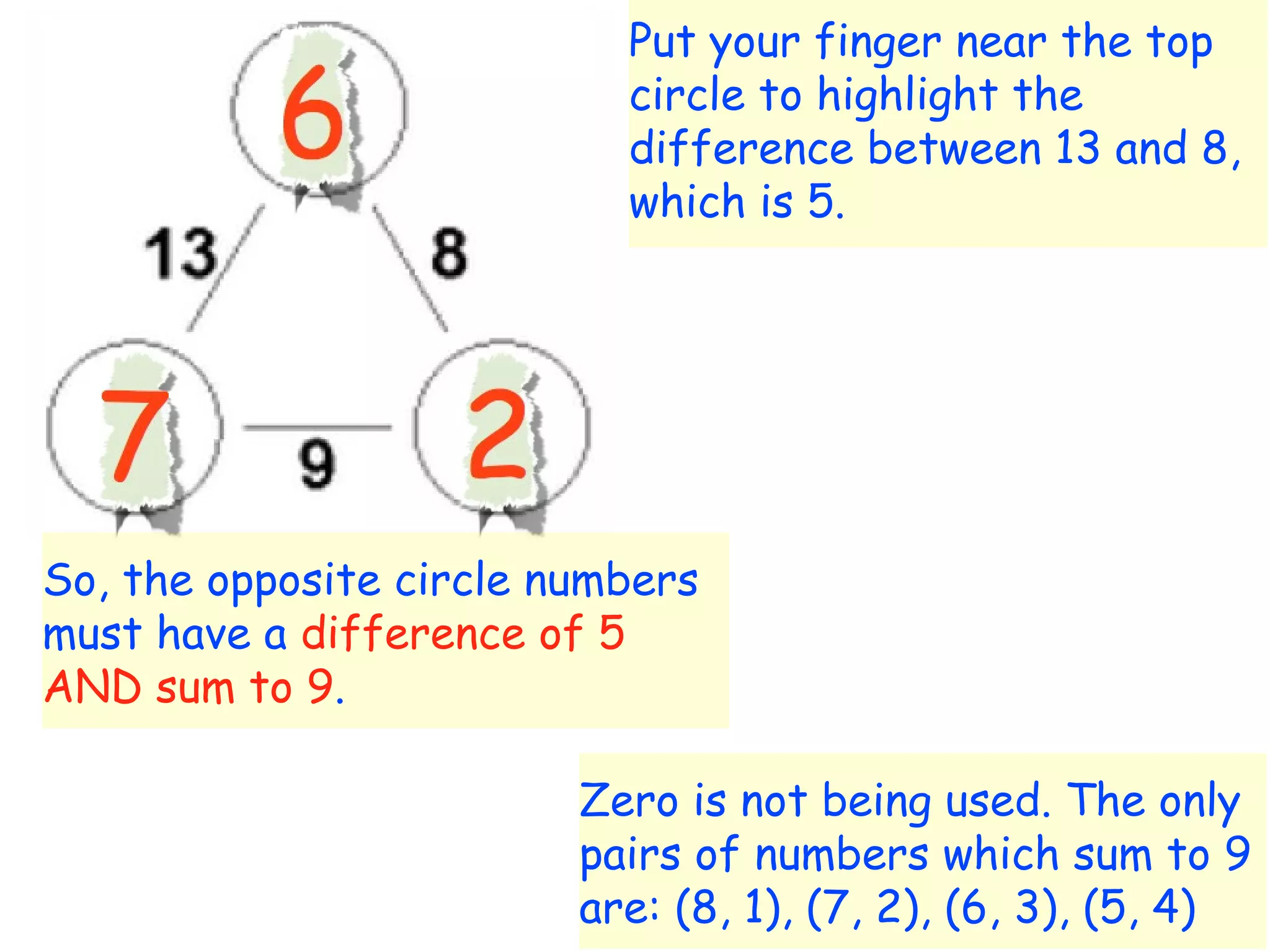
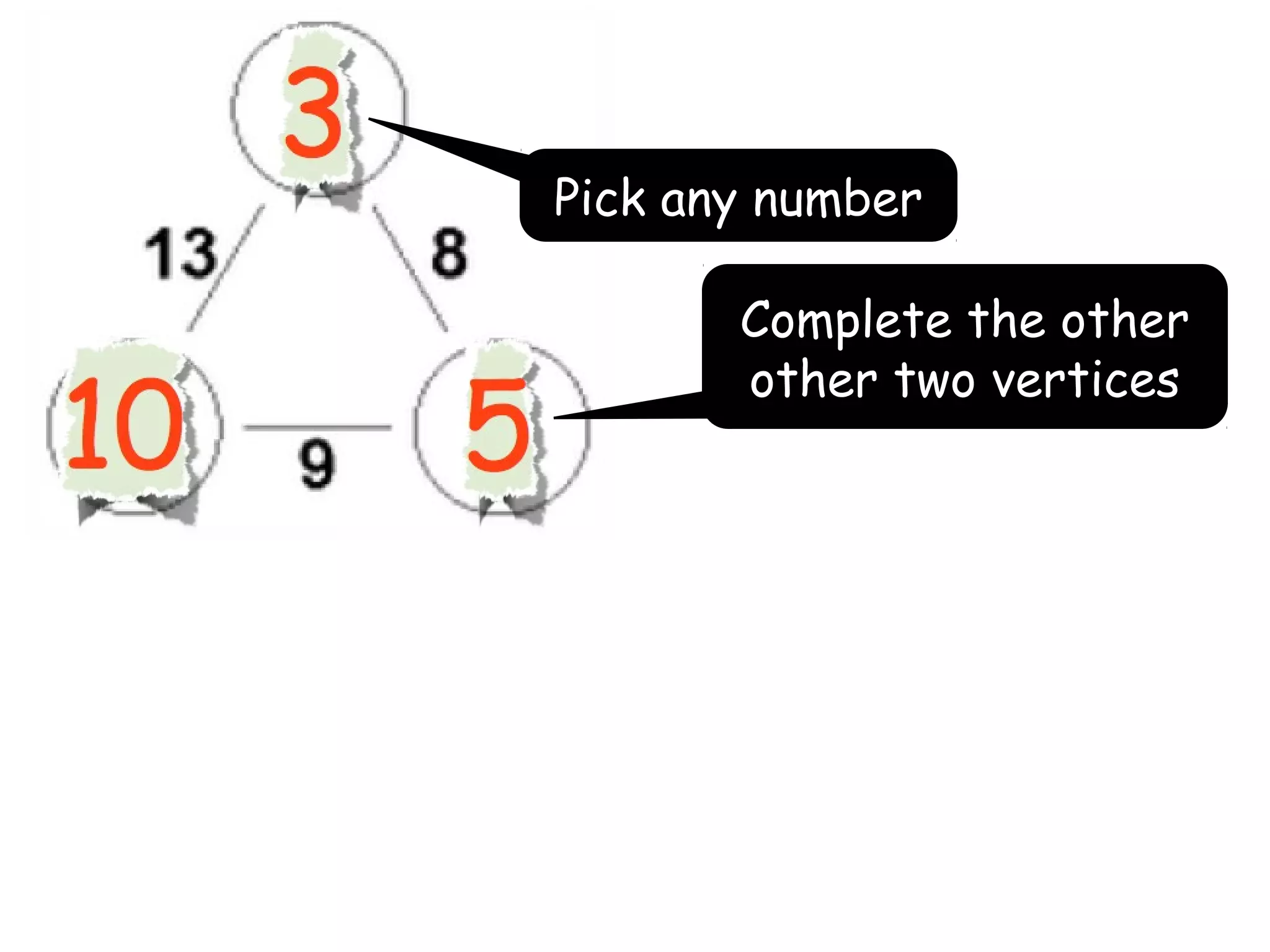
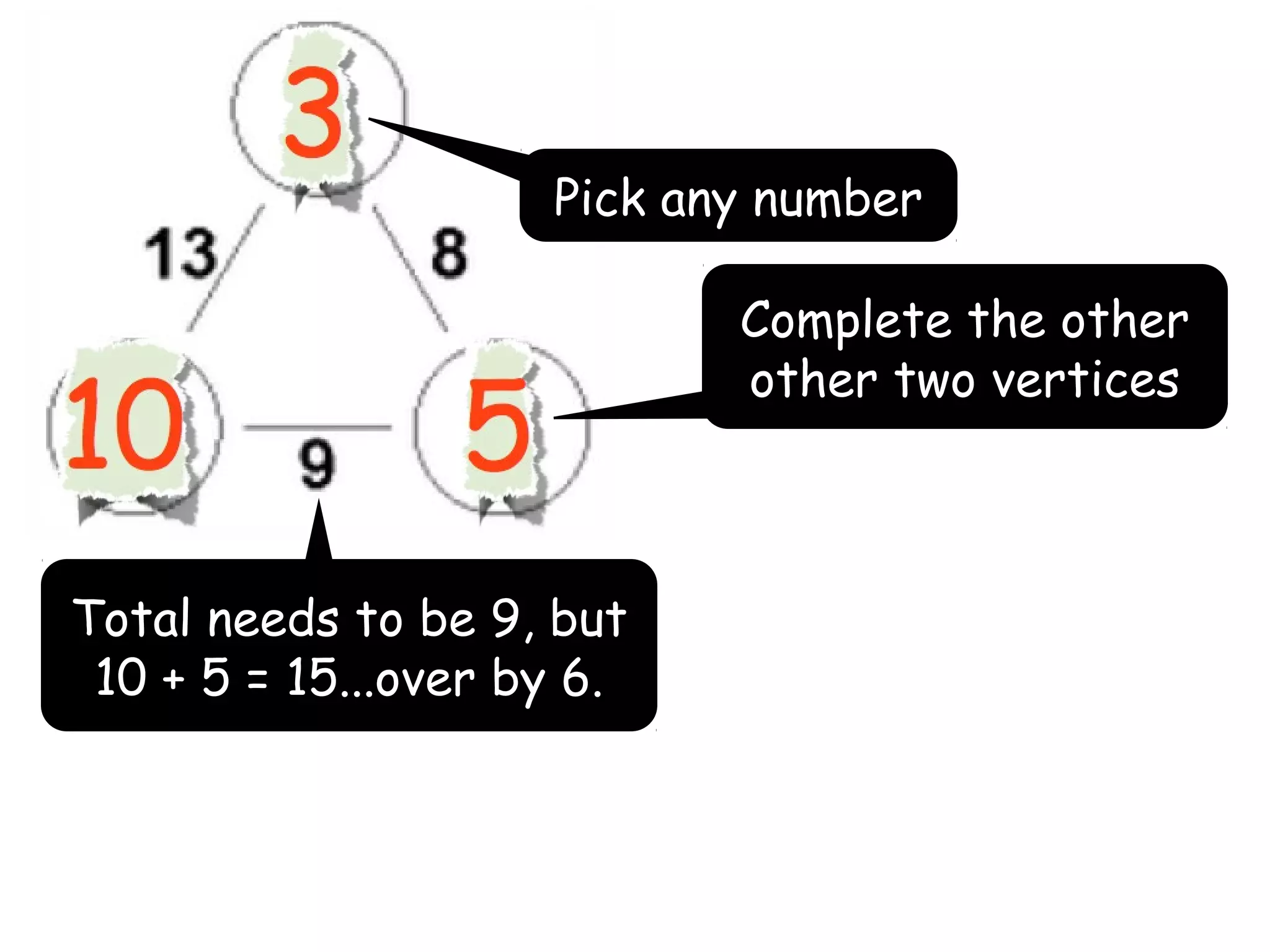
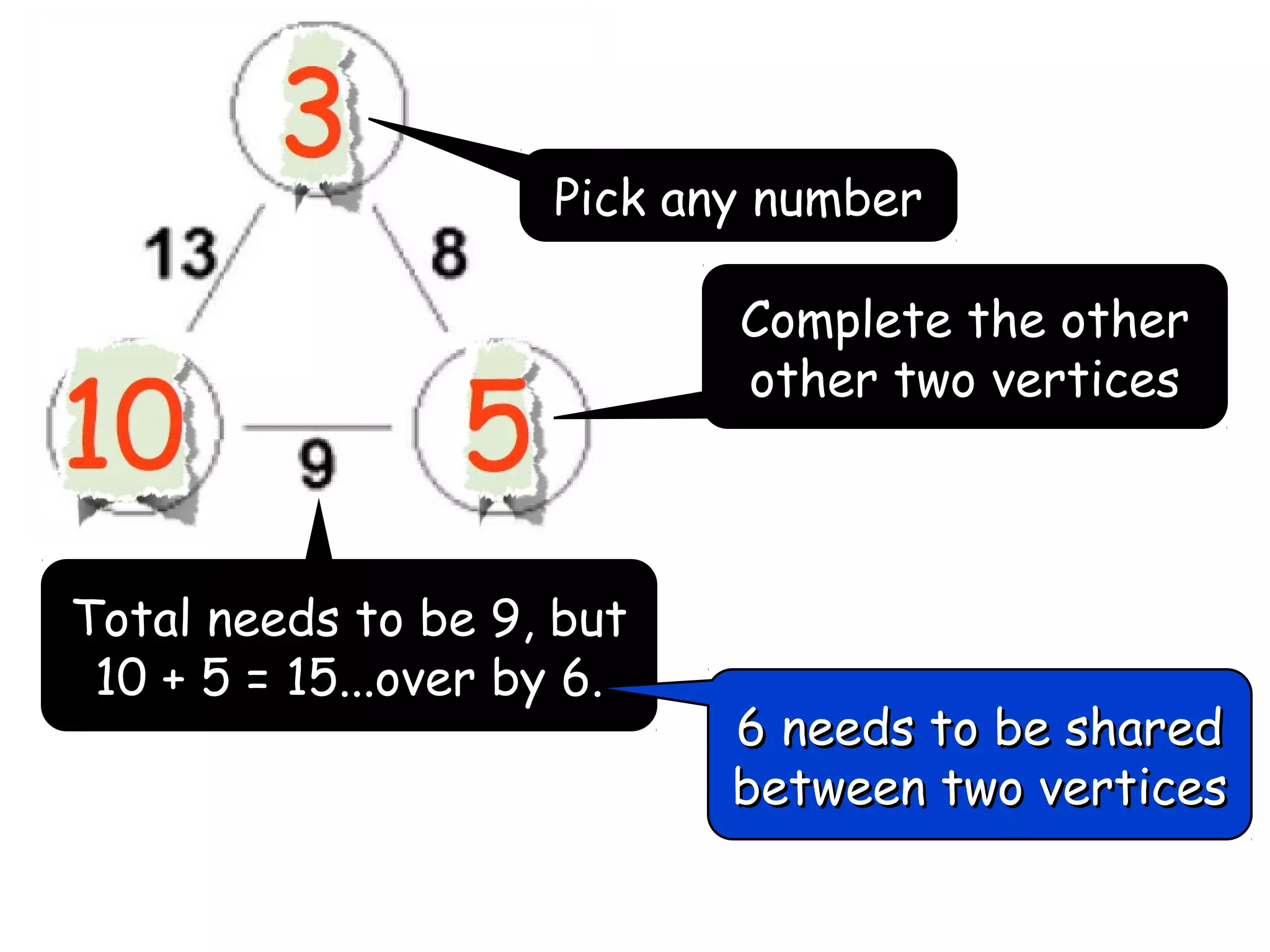
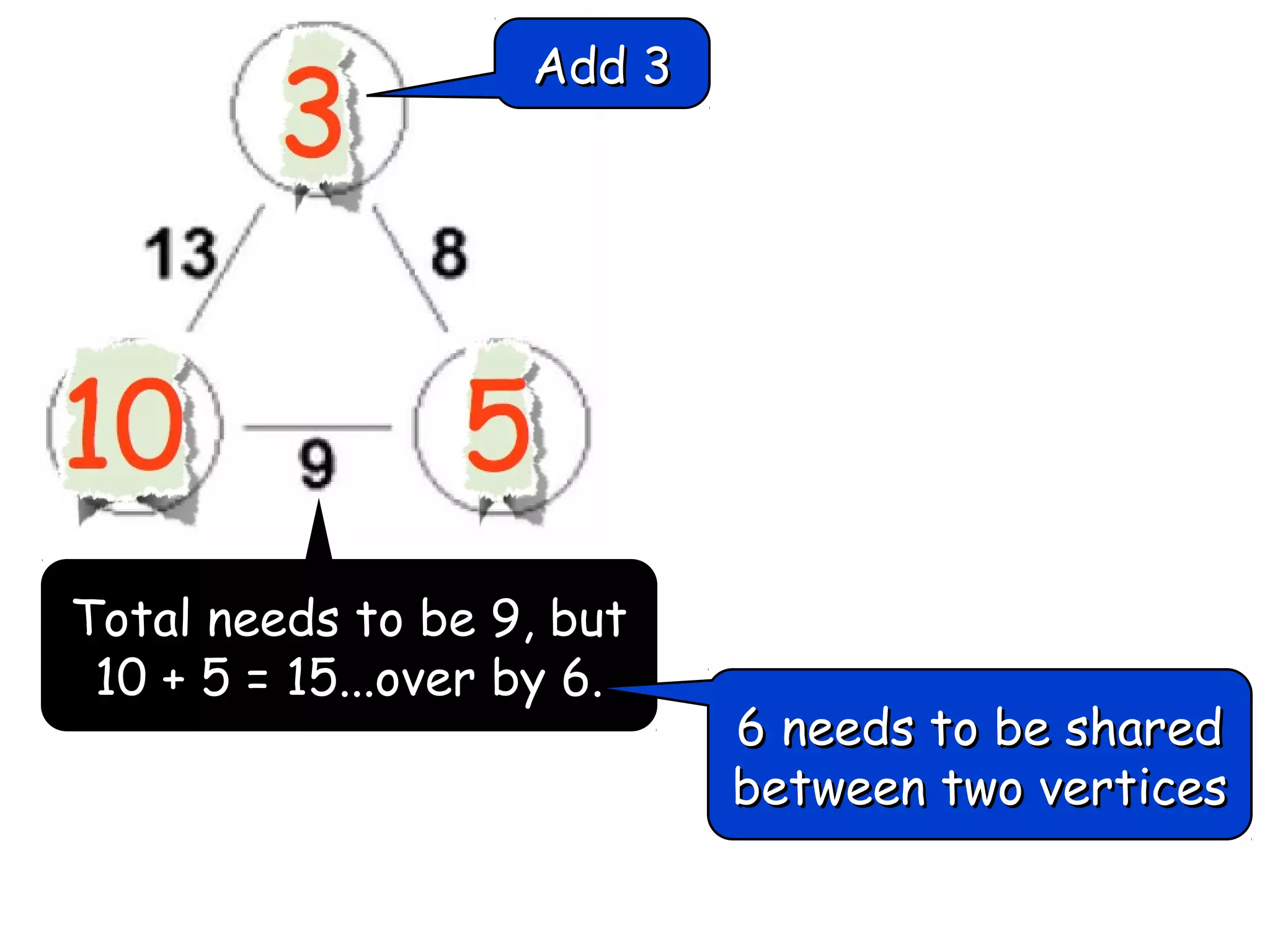
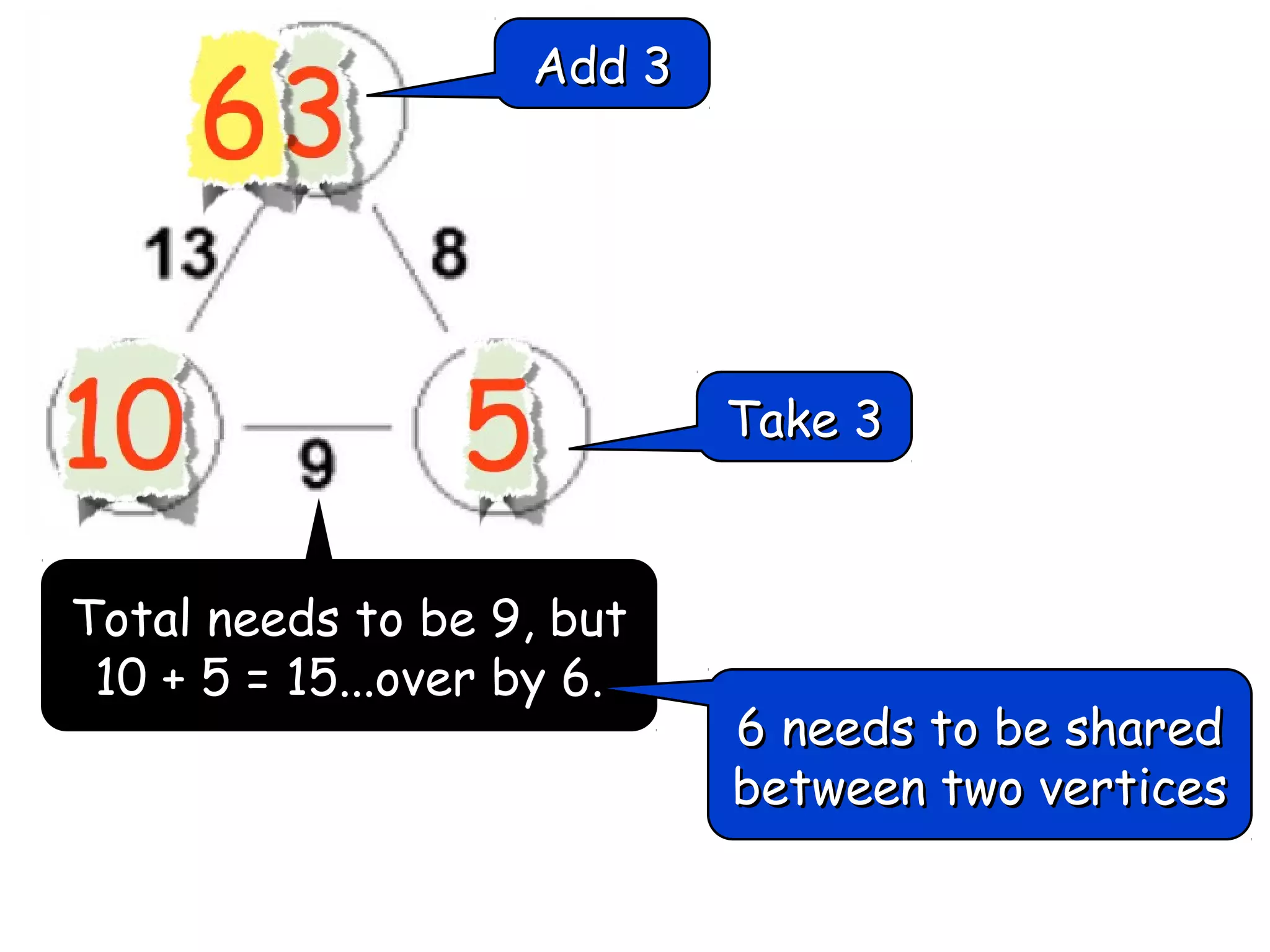
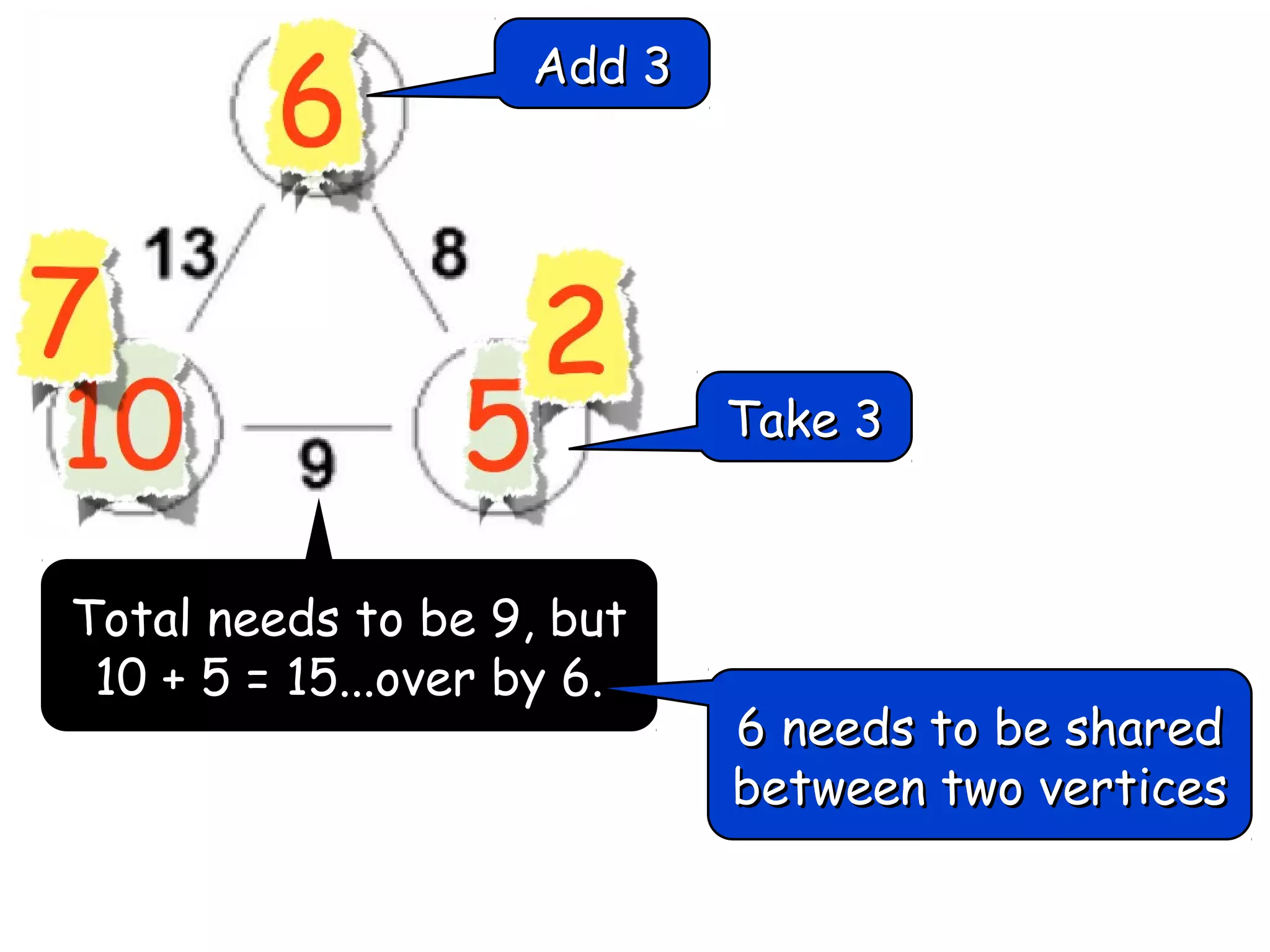
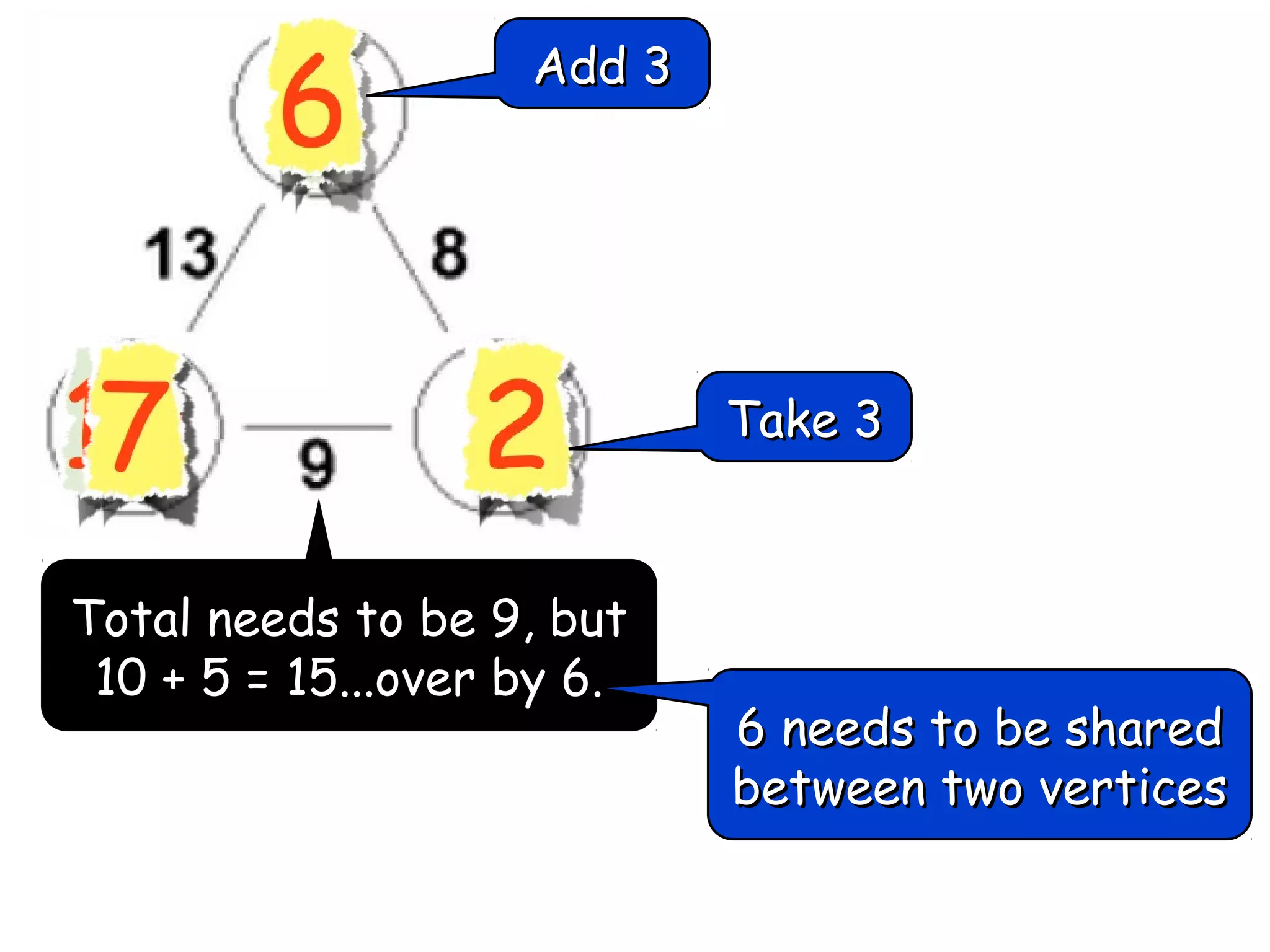
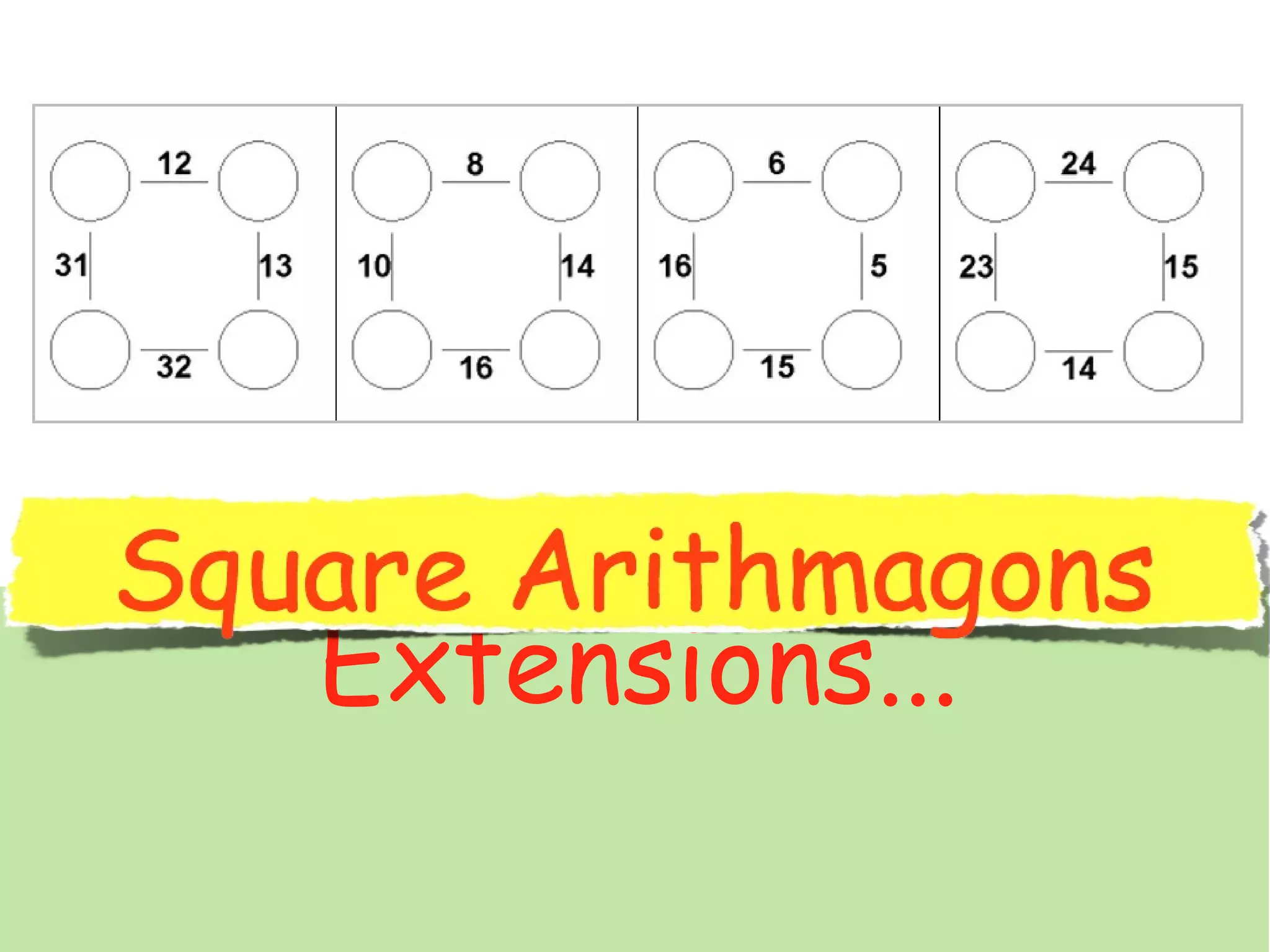
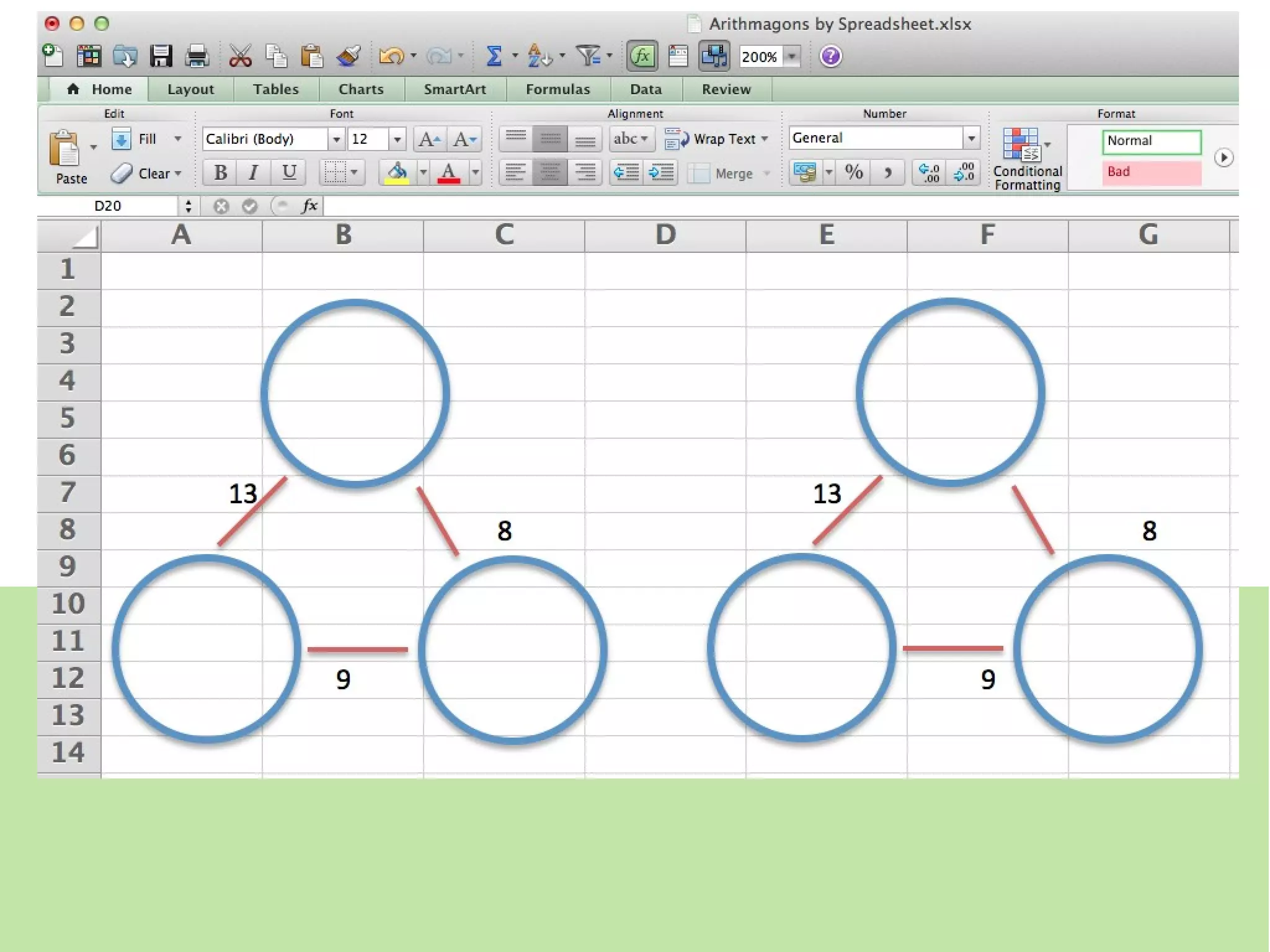
The document discusses mathematical problem-solving techniques using a structure called arithmagons, which focuses on relationships between numbers on edges and vertices. It emphasizes concepts like addition, algebraic representation, and problem posing through interactive challenges that engage students in critical thinking. Additionally, it includes strategies for older students to further develop their skills by programming related challenges.

1. Exploring mathematical problems
beyond the tip of the iceberg

4. Exploring mathematical
problems
beyond the tip of the
iceberg

5. Pick problems...

6. Pick problems...

7. maths300.esa.edu.au

8. maths300.esa.edu.au

9. Attributes of a
Maths 300 lesson
maths300.esa.edu.au

11. Challenges in my classroom...

12. Arithmagons

13. Strategy Board

20. Arithmagons
Learning outcomes and related concepts
•basic addition
•difference between
•algebraic representation
•problem posing and solving
•

25. Pen
thickness
Pen colour

27. t1 = a + b
t2 = b + c
t3 = a + c

28. t1 = a + b
t2 = b + c
t3 = a + c
The number on the edge is
the sum of the two numbers
on the vertices.

29. t1 = a + b
t2 = b + c
t3 = a + c
t1 - t2 = (a + b) - (b - c)
this becomes
t1 - t2 = a - c

30. t1 = a + b
t2 = b + c
t3 = a + c
t1 - t2 = (a + b) - (b - c)
this becomes
t1 - t2 = a - c

31. Put your finger near the top circle to
highlight the difference between 13 and 8,
which is 5.

32. Put your finger near the top
circle to highlight the
difference between 13 and 8,
which is 5.
So, the opposite circle numbers
must have a difference of 5
AND sum to 9.

33. Put your finger near the top
circle to highlight the
difference between 13 and 8,
which is 5.
So, the opposite circle numbers
must have a difference of 5
AND sum to 9.
Zero is not being used. The only
pairs of numbers which sum to 9
are: (8, 1), (7, 2), (6, 3), (5, 4)

34. Put your finger near the top
circle to highlight the
difference between 13 and 8,
which is 5.
So, the opposite circle numbers
must have a difference of 5
AND sum to 9.
Zero is not being used. The only
pairs of numbers which sum to 9
are: (8, 1), (7, 2), (6, 3), (5, 4)

35. Put your finger near the top
circle to highlight the
difference between 13 and 8,
which is 5.
So, the opposite circle numbers
must have a difference of 5
AND sum to 9.
Zero is not being used. The only
pairs of numbers which sum to 9
are: (8, 1), (7, 2), (6, 3), (5, 4)

36. Pick any number
Another approach...

37. Pick any number
Complete the other
other two vertices

38. Pick any number
Complete the other
other two vertices
Total needs to be 9, but
10 + 5 = 15...over by 6.

39. Pick any number
Complete the other
other two vertices
Total needs to be 9, but
10 + 5 = 15...over by 6.
6 needs to be shared
between two vertices

40. Add 3
Total needs to be 9, but
10 + 5 = 15...over by 6.
6 needs to be shared
between two vertices

41. Add 3
Take 3
Total needs to be 9, but
10 + 5 = 15...over by 6.
6 needs to be shared
between two vertices

42. Add 3
Take 3
Total needs to be 9, but
10 + 5 = 15...over by 6.
6 needs to be shared
between two vertices

43. Add 3
Take 3
Total needs to be 9, but
10 + 5 = 15...over by 6.
6 needs to be shared
between two vertices

44. Extensions...

45. Extensions...

46. Challenge older kids to program a SS

47. Challenge older kids to program a SS