The Presentation Contains Basics regarding Circular Motion

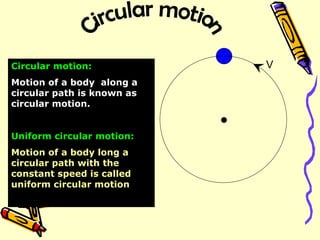
1. V Circular motion: Motion of a body along a circular path is known as circular motion. Uniform circular motion: Motion of a body long a circular path with the constant speed is called uniform circular motion . Circular motion

3. r F V For uniform circular motion body needs a lateral force such that it continuously changes its direction, this force is called centripetal force. Centripetal force: Centripetal force is defined as the radial force directed towards the center acting on a body in circular motion. Centripetal force Circular motion

5. r F V The centripetal force –f acting on a body of mass - m moving in a circular path is given by , Centripetal force Centripetal acceleration: Circular motion

9. STOP r o F V Circular motion What happens if the centripetal is stopped when the body is moving in a circular path? If the centripetal force is stopped the body moves along the tangent to the circle.

10. r o Circular motion If the centripetal force is stopped the body moves along the tangent to the circle with a velocity-v. WHY????? v This is in accordance with Newton’s first law of motion. When there is no centripetal force then there can not be any change in direction of the body hence it moves in a straight line along the tangent to the circle.