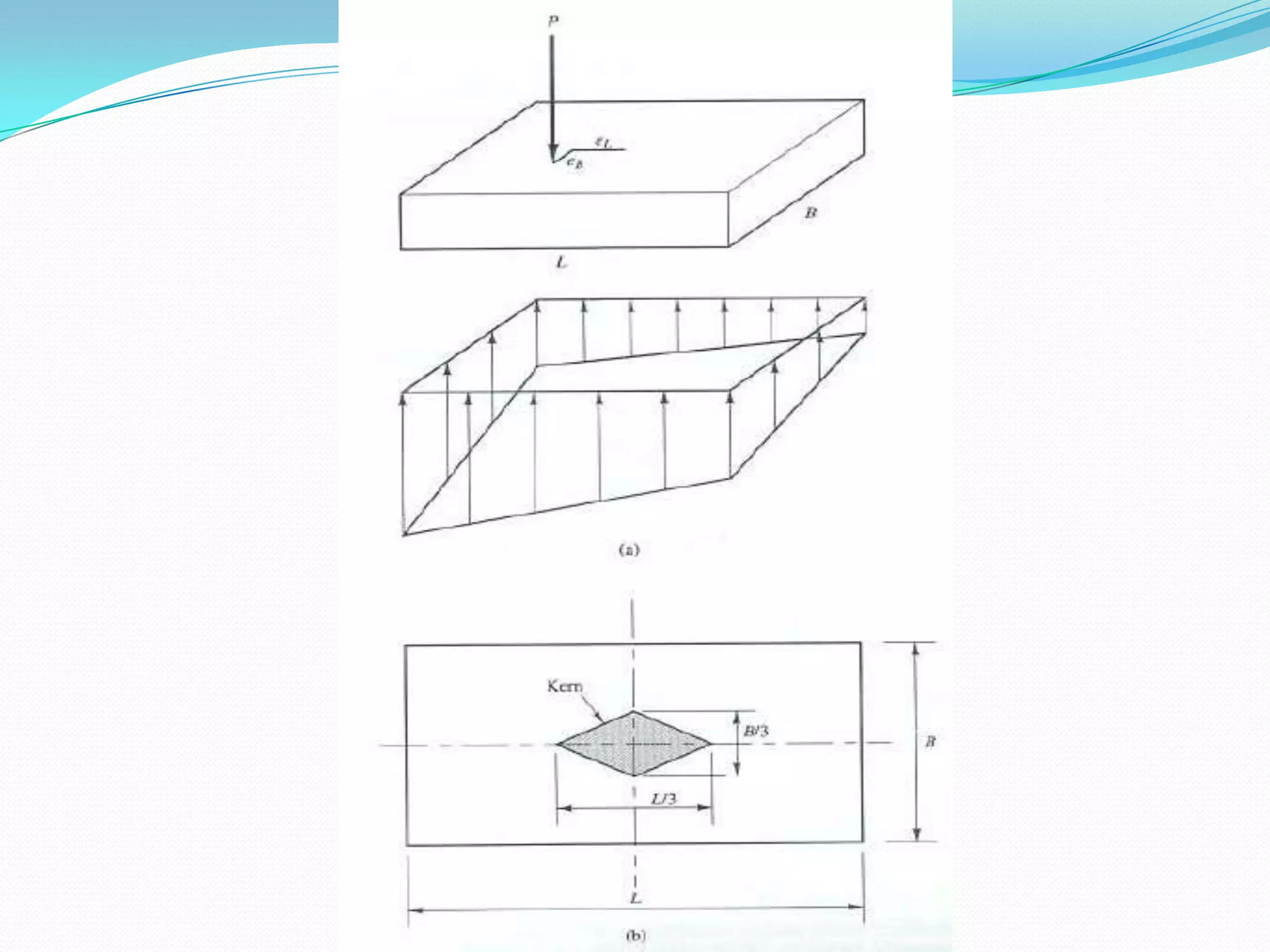
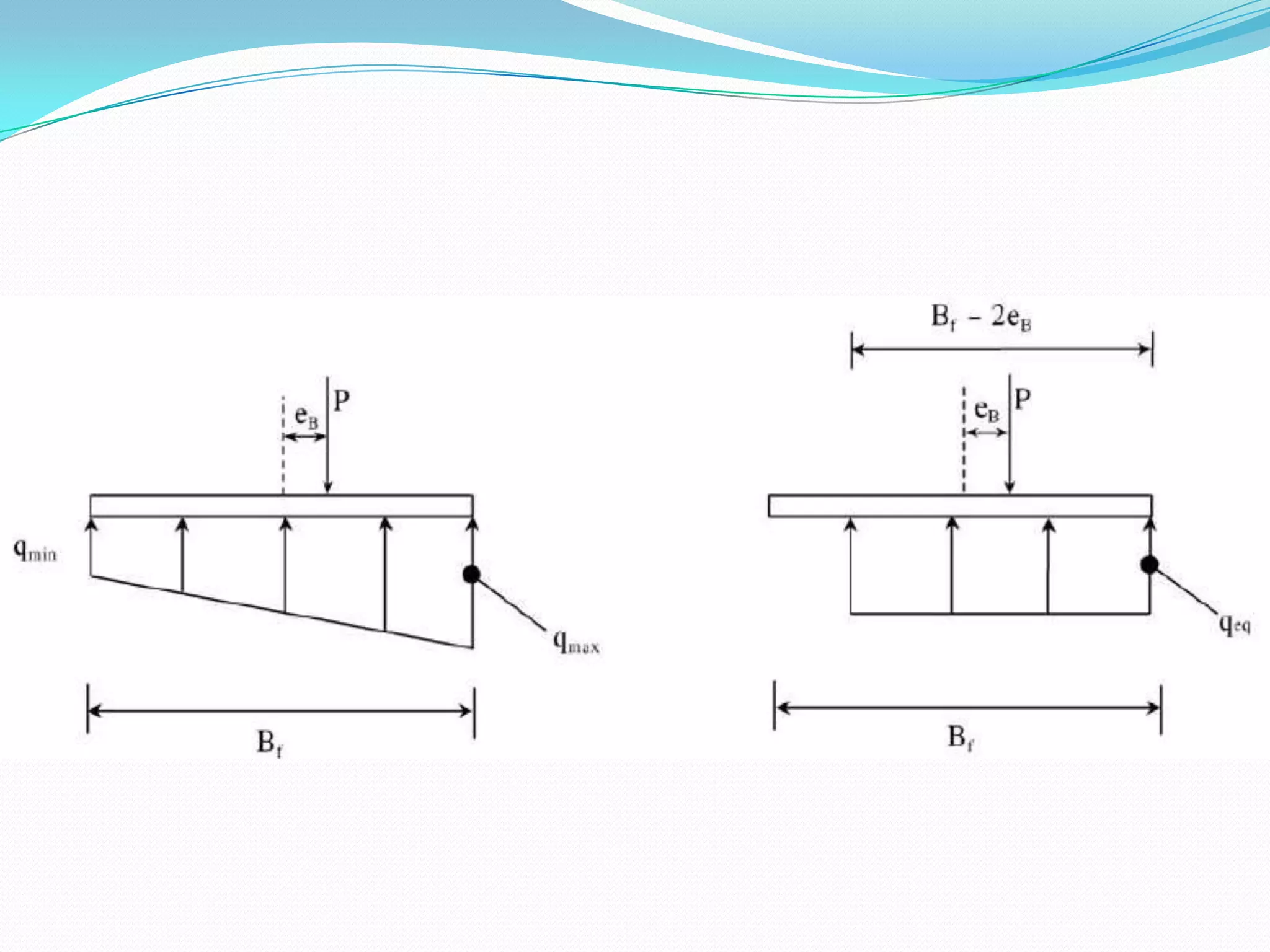
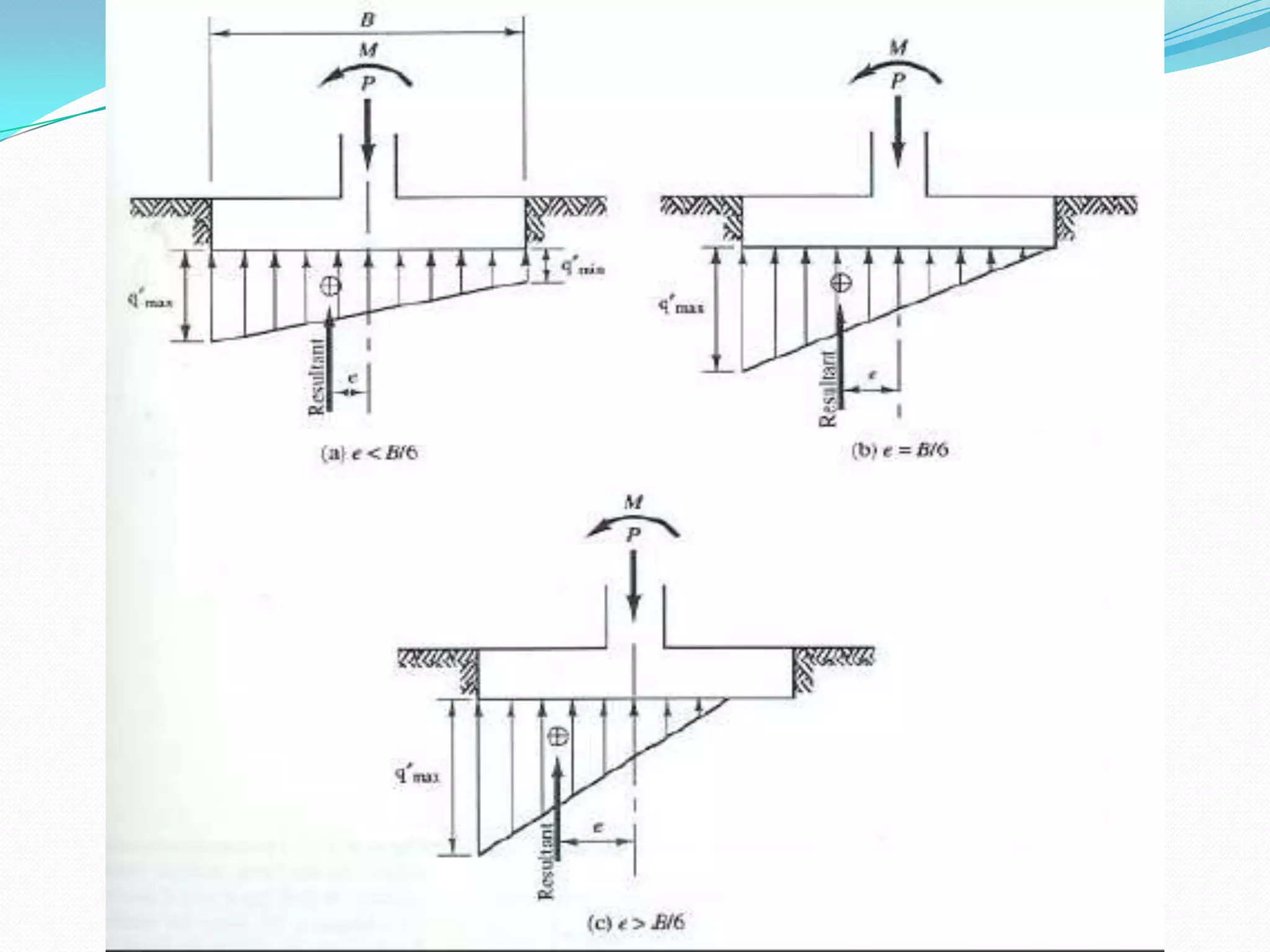
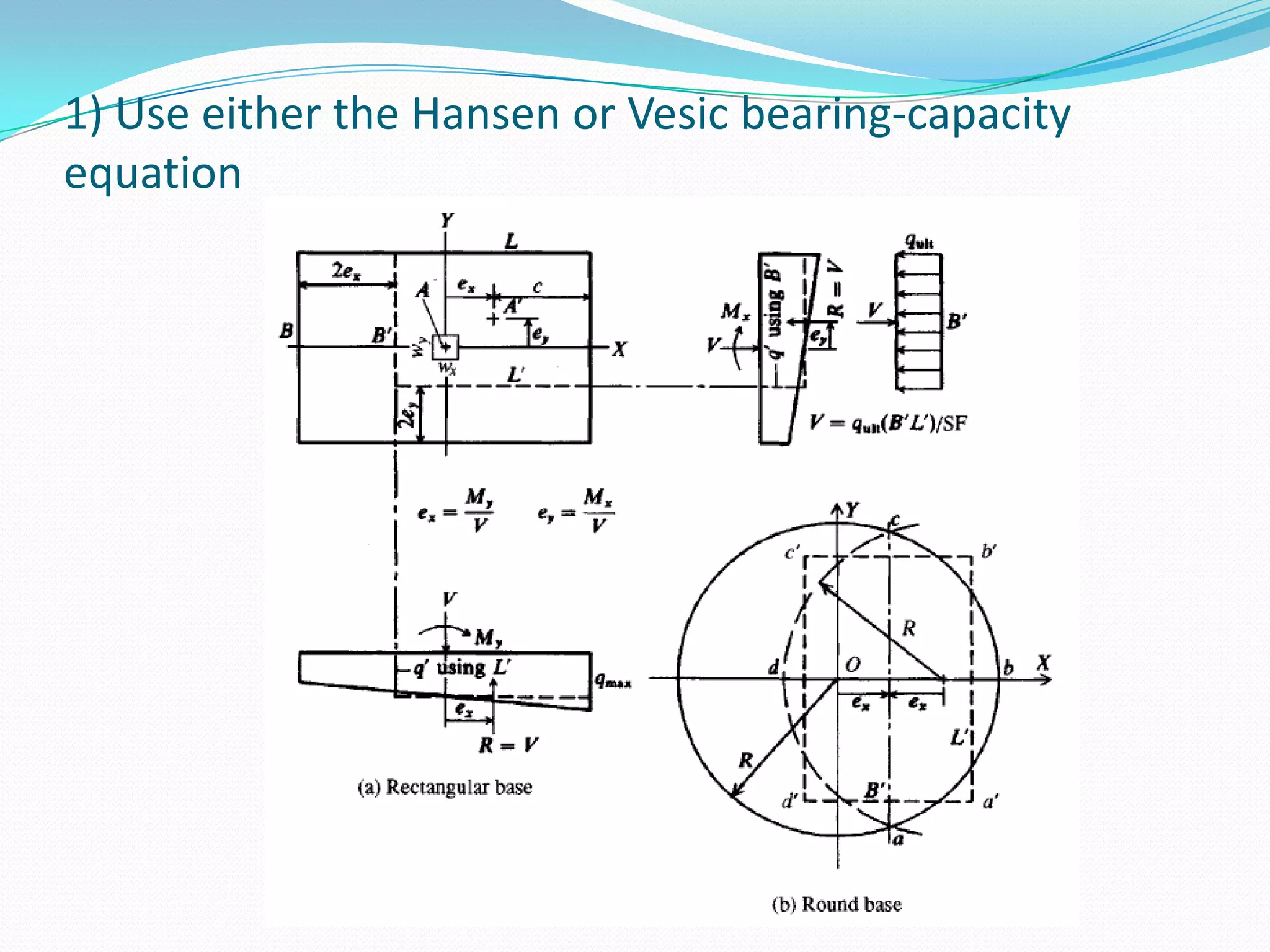
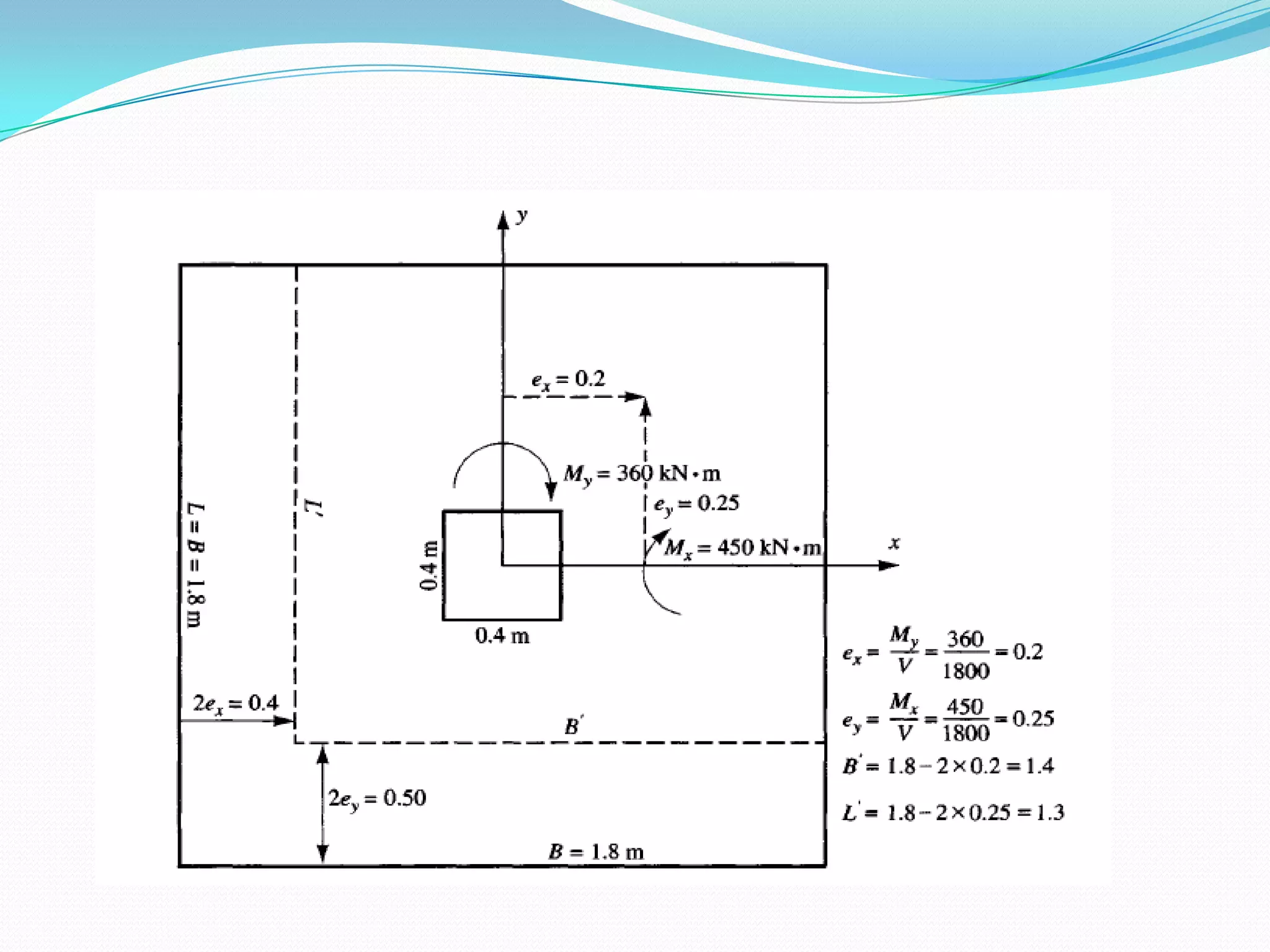
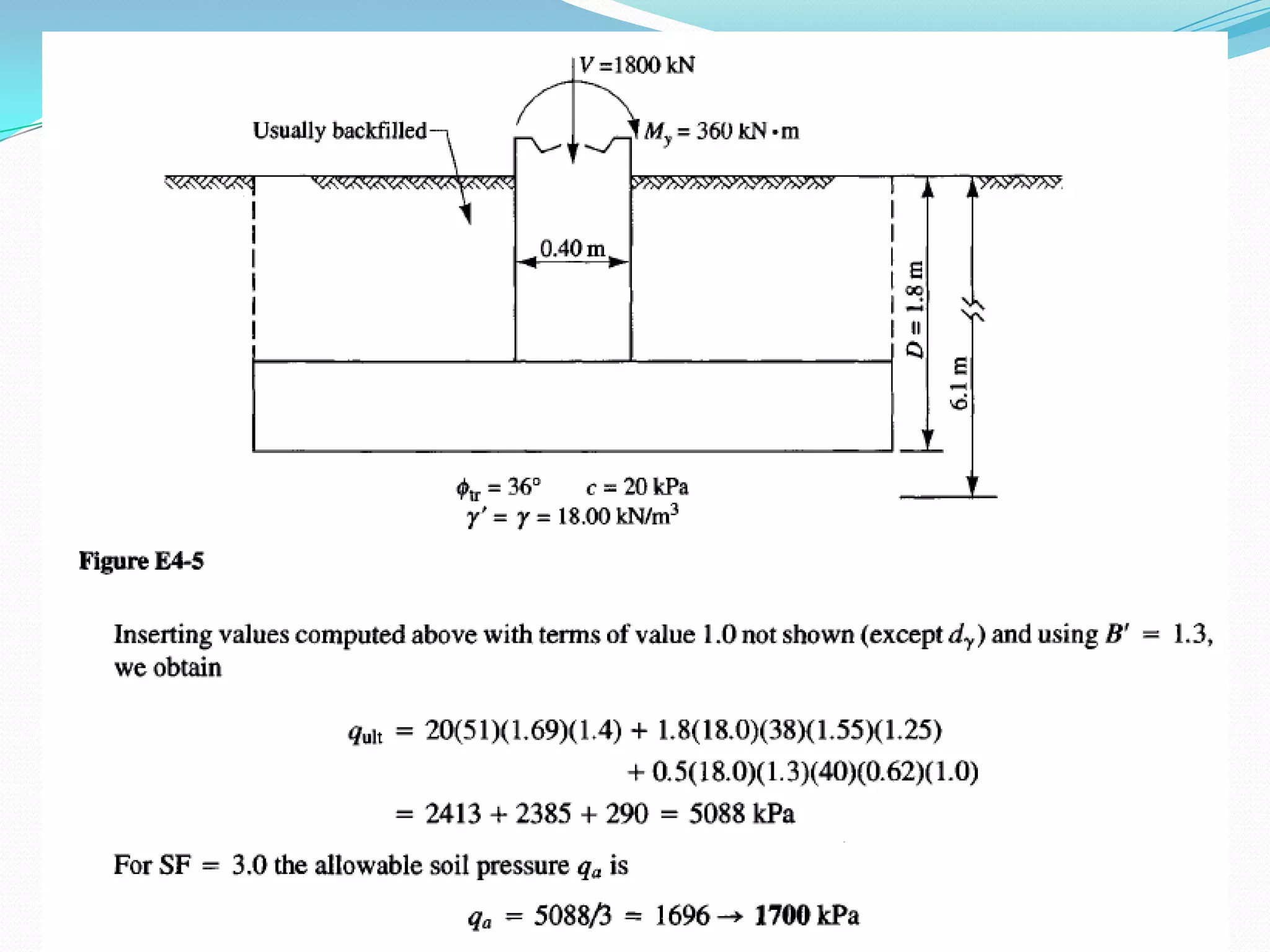
This document discusses how to account for the effects of eccentric loads on the design of rectangular footings. It provides equations to calculate the modified width and length of a footing based on the load eccentricities. It also provides the minimum footing dimensions required for a central column and describes how to calculate the ultimate bearing capacity of an eccentric footing using either the Hansen/Vesic or Meyerhof methods.

1. ECCENTRIC LOADBy : CrystinPanjaitanEdwin SeranoEkiSinagaRicky Bancin

2. Pengaruhmomenlenturpadadayadukungdapatdiperkirakandenganmengubahmomenlenturpadaeksentrisitasekivalen (e).

3. Kemudiandimensifondasitelapakdiperkeciluntukmemperhitungkanpengaruheksentrisitas yang merugikan, denganpenjelasansebagaiberikut :Pengaruhdimensifondasitelapakdapatdihitungdenganpersamaan:L' = L - 2ex (modified width)

4. B' = B - 2ey (modified length)

5. ex = (eccentricities in the directions of length)

6. ey = (eccentricities in the directions of width) Dimana ;B : lebarpondasiB’ : lebarefektifpondasiL : panjangpondasiL’ : panjangefektifpondasie: eksentrisitasbebanresultanpadadasarpondasiMx = momenlentursejajardenganlebarfondasi, B (ton.matauKN/m)My = momenlentursejajardenganpanjangfondasi, B (ton.matauKN/m)P = beban (ton atau KN)

9. For design the minimum dimensions of a rectangular footing with a central column of dimensions “Wx x Wy”are required to beBmin = 4ey + Wy B’ = 2ey + WyLmin = 4ex + Wx B’ = 2ex + Wx

11. 2) Bebanbatas yang bekerjapadafondasitelapakmenimbulkankeruntuhandukungsebagaiberikut:Pu = qultB’L’

12. The ultimate bearing capacity for footings with eccentricity, using either the Meyerhof or Hansen/Vesic equations, is found in either of two ways:

13. 1) Use either the Hansen or Vesic bearing-capacity equation

14. a. Use B' in the yBNy term.b. Use B' and L' in computing the shape factors.c. Use actual B and L for all depth factors.The computed ultimate bearing capacity qult is then reduced to an allowable value qa with an appropriate safety factor SF as (and Pa = qaB'L')qa = qult/ SF

15. 2) Use the Meyerhof general bearing-capacity equation and a reduction factor Re

27. THANK YOU… ^^