This document discusses conformal field theories and three point functions. It begins by introducing conformal field theories and noting that three point functions of stress tensors are constrained by conformal invariance. For parity even CFTs in d=4 dimensions, the three point functions of the stress tensor T can be written in terms of coefficients that correspond to effective numbers of scalars, fermions, and vectors. Positivity of energy flux from collider experiments imposes constraints on these coefficients. The document then discusses extending such analyses to parity violating CFTs in d=3 dimensions, where the three point functions of the stress tensor T and conserved current j contain both parity even and odd terms. It proposes studying modifications to existing constraints from applying coll

1. Conformal field theories and three point functions
Subham Dutta Chowdhury
October 4, 2017
University of Chicago, 2017
Subham Dutta Chowdhury Conformal field theories and three point functions 1/51

2. References
S. D. Chowdhury, J. R. David and Shiroman Prakash, “Spectral sum rules for
conformal field theories in arbitrary dimensions”, JHEP07(2017)119.
S. D. Chowdhury, J. R. David and S. Prakash, “Constraints on parity violating
conformal field theories in d = 3”, [arXiv:1707.03007[hep-th]].
Ongoing Work.
Subham Dutta Chowdhury Conformal field theories and three point functions 2/51

3. Introduction and motivation
Conformal field theories in are of interest both in the context of holography as
well as in condensed matter physics.
Three point functions of stress tensors, for example, are completely fixed by
conformal invariance upto three independent parameters (two for d = 3)
There has been a systematic study of possible constraints on these (parity
invariant) parameters in d ≥ 3 dimensions.
Subham Dutta Chowdhury Conformal field theories and three point functions 3/51

4. Consider a conformal field theory with a conserved stress tensor T in d = 4.
Conformal invariance restricts the structure of the three point functions of T,
to be of the following form,
TTT = nT
s TTT free boson + nT
f TTT free fermion + nT
v TTT vector,
where .. free boson, .. free fermion denote the correlator a real free boson and a
real free fermion respectively, while .. vector refers to the vector boson.
[Osborn, Petkou 1994]
The numerical coefficients nT
s , nT
f and nT
v correspond to effective number of
scalars, fermions and vector bosons respectively.
Note that in higher dimensions, nT
v corresponds to correlation functions of
k-forms and is non zero only for even dimensions.
Subham Dutta Chowdhury Conformal field theories and three point functions 4/51

5. For parity even conformal field theories in d = 4 and higher dimensions,
conformal collider bounds impose constraints on the parity even coefficients
that occur in the three point functions.
[Maldacena, Hofman 2008]
[De Boer et al , Sinha et al. 2009]
This involves studying the effect of localized perturbations at the origin. The
integrated energy flux per unit angle, over the states created by such
perturbations, is measured at a large sphere of radius r.
Eˆn =
0|O†
EˆnO|0
0|O†O|0
,
Eˆn = lim
r→∞
r2
∞
−∞
dtni
Tt
i (t, rˆn),
O ∼
ij
Tij
ijTij|Tij
ij
,
i
ji
jjj|ji
i
,
(1)
where, ˆn is a unit vector in R3
, which specifies the direction of the calorimeter
and O is the operator creating the localised perturbation.
Subham Dutta Chowdhury Conformal field theories and three point functions 5/51

6. By demanding the positivity of energy flux, one obtains various constraints on
the parameters of the three point function of the CFT, depending on the
operators used to create the states O
The positivity of energy flux then translates to the following bounds,
−
t2
3
−
2t4
15
+ 1 ≥ 0,
2 −
t2
3
−
2t4
15
+ 1 + t2 ≥ 0,
3
2
−
t2
3
−
2t4
15
+ 1 + t2 + t4 ≥ 0, (2)
where,
t2 =
15(nT
f − 4nT
v )
3nT
f + nT
s + 12nT
v
, t4 =
15(−2nT
f + nT
s + 2nT
v )
2(3nT
f + nT
s + 12nT
v )
. (3)
In other words,
nT
s ≥ 0, nT
v ≥ 0, nT
f ≥ 0 (4)
Subham Dutta Chowdhury Conformal field theories and three point functions 6/51

7. For parity invariant theories in general dimensions, causality constraints in
terms of these variables is given by
[Camanho, Edelstein 2009]
1 −
1
d − 1
t2 −
2
(d + 1)(d − 1)
t4 ≥ 0, (5)
1 −
1
d − 1
t2 −
2
(d + 1)(d − 1)
t4 +
1
2
t2 ≥ 0,
1 −
1
d − 1
t2 −
2
(d + 1)(d − 1)
t4 +
d − 2
d − 1
(t2 + t4) ≥ 0.
Can such constraints be used to put bounds on physical quantities of CFTs at
finite temperature?
Moreover, physically relevant examples of confromal field theories, in d = 3,
need not preserve parity owing to the presence of a parity violating chern
simons term.
Subham Dutta Chowdhury Conformal field theories and three point functions 7/51

8. Let us consider a conformal field theory in d = 3 with a U(1) conserved current
j and conserved stress tensor T and let the theory be parity violating.
Conformal invariance restricts the structure of the three point functions of j
and T, in d = 3, to be of the following form,
jjT = nj
s jjT free boson + nj
f jjT free fermion + pj jjT parity odd, (6)
TTT = nT
s TTT free boson + nT
f TTT free fermion + pT TTT parity odd,
where, as before, .. free boson, .. free fermion denote the correlator a real free
boson and a real free fermion respectively, while .. parity odd refers to the
parity odd structure.
[Osborn, Petkou 1994]
[Giombi, Prakash, Yin 2011]
The numerical coefficients nj,T
s , nj,T
f correspond to the parity invariant sector,
while pj,T is the parity violating coefficient. The parity violating structure is
unique to d = 3 and it appears only for interacting theories.
Subham Dutta Chowdhury Conformal field theories and three point functions 8/51

9. For parity even theories in d = 3, the collider bounds become,
1 −
t4
4
≥ 0
1 +
t4
4
≥ 0 (7)
where,
t4 = −
4(nT
f − nT
s )
nT
f + nT
s
,
(8)
For a general conformal field theory in d = 3, can there be modifications to
these constraints on the parameter space (both parity even and parity odd) of
three point functions from conformal collider analysis?
Subham Dutta Chowdhury Conformal field theories and three point functions 9/51

10. Positivity of energy flux
Let us consider localised perturbations of the CFT in minkowski space.
ds2
= −dt2
+ dx2
+ dy2
. (9)
The perturbations evolve and spread out in time. In order to measure the flux,
we consider concentric circles.
The energy measured in a direction (denoted by ˆn) is defined by,
Eˆn = lim
r→∞
r
∞
−∞
dt ni
Tt
i (t, rˆn), (10)
where r is the radius of the circle on which the detector is placed and ˆn is a unit
vector which determines the point on the circle where the detector is placed.
The expectation value of the energy flux measured in such a way should be
positive for any state.
[Maldacena, Hofman 2008]
Eˆn ≥ 0. (11)
Subham Dutta Chowdhury Conformal field theories and three point functions 10/51

11. We can also consider the detector to be placed at null infinity from the very
beginning and integrate over the null working time. The two definitions are
equivalent.
[Zhiboedov 2013]
In order to calculate energy flux at null infinity, we introduce the light cone
coordinates, x±
= t ± y. We place our detector along y direction. The energy
functional becomes
E =
∞
−∞
dx−
2
lim
x+→∞
(
x+
− x−
2
)T−−. (12)
We are interested in expectation value of the energy operator on states created
by stress tensor or current with specific polarizations.
Subham Dutta Chowdhury Conformal field theories and three point functions 11/51

12. The normalized states are defined as
OE|0 =
dtdxdy eiEt
O(t, x, y)|0
OE|OE
,
(13)
where O are operators constructed from the current or stress tensor with
definite polarizations.
We look at perturbations created by stress tensor and current insertions
O( ; T) = ijTij
, or O( ; j) = iji
. (14)
We demand that energy flux measured in such a way be positive,
E =
0|O†
EO|0
0|O†O|0
≥ 0. (15)
Subham Dutta Chowdhury Conformal field theories and three point functions 12/51

13. Energy matrix for charge excitations
Let us look at the states created by current excitations first. We choose two
independent polarisations for the charge excitations,
x
= 1, y
= 1. (16)
This results in the following energy matrix
ˆE(j) =


0|O†
E( ; j)EOE( ; j)|0 0|O†
E( ; j)EOE( ; j)|0
0|O†
E( ; j)EOE( ; j)|0 0|O†
E( ; j)EOE( ; j)|0

 .
As an example let us see one such matrix element written out explicitly
0|O†
E( ; j)EOE( ; j)|0 =
1
OE( ; j)|OE( , j)
× (17)
d3
xeiEt
lim
x+
1 →∞
x+
1 − x−
1
4
dx−
1 jx(x)T−−(x1)jx(0) ,
where
OE( ; j)|OE( , j) = d3
xeiEt
jx(t, x, y)jx(0). (18)
Subham Dutta Chowdhury Conformal field theories and three point functions 13/51

14. The condition of positivity of energy functional measured by the calorimeter
then translates to demanding that the eigenvalues of the energy matrix be
positive.
The basic ingredient in this computation is the three point function of the
stress energy tensor including the parity odd term.
j(x)T(x1)j(0) =
1
|x1 − x|3|x1|3|x|
σ
2 Iα
σ (x − x1) ρ
3Iβ
ρ (−x1) µν
1 tµναβ(X)
+pj
Q2
1S1 + 2P2
2 S3 + 2P2
3 S2
|x1 − x||x|| − x1|
, (19)
where pj is the parity odd coefficient.
[Osborn, Petkou 1994]
[Giombi, Prakash, Yin 2011]
The first line corresponds to the usual parity even contribution while the 2nd
part is the parity odd contribution to the three point function.
Subham Dutta Chowdhury Conformal field theories and three point functions 14/51

15. For normalising the excited states, we also need the two point function of
currents which is given by
jµ(x)jν (0) =
CV
x4
Iµν (x), (20)
with
CV =
8
3
π(c + e), (21)
where
c =
3(2nj
f + nj
s)
256π3
, e =
3nj
s
256π3
(22)
The parity even part contributes to the diagonal elements of the energy matrix
while the off-diagonal contribution is due to the parity violating part.
Subham Dutta Chowdhury Conformal field theories and three point functions 15/51

16. We look at the contribution to the energy matrix corresponding to the
following parity violating term in the three point function,
pjQ2
1S1
|x1 − x||x|| − x1|
,
(23)
where,
Q2
1 = µ
1
ν
1
x1µ
x2
1
−
x1µ − xµ
(x1 − x)2
x1ν
x2
1
−
x1ν − xν
(x1 − x)2
,
S1 =
1
4|x1 − x||x|3| − x1|
εµν
ρxµ(x1 − x)ν
ρ
2
α
3 xα
−
εµ
νρ
2
|x1 − x|2
xµ + |x|2
(x1 − x)µ
ν
2
ρ
3 . (24)
Subham Dutta Chowdhury Conformal field theories and three point functions 16/51

17. Recall that the parity odd terms contribute to the off diagonal elements of the
energy functional. The appropriate choice of polarisations is therefore,
x
2 = y
3 = −−
1 = 1. (25)
We are looking at essentially the following quantity.
jx(x)T−−(x1)jy(0) . (26)
For such a choice of polarisations, the parity violating term can be explicitly
written out to be,
I = pj
Q2
1S1
|x1 − x||x|| − x1| −−
1 = x
2 =
y
3 =1
,
=
16pj
64|x1 − x|2|x|4| − x1|2
x1−
x2
1
−
(x1 − x)−
(x1 − x)2
2
εµν
xxµ(x1 − x)ν (x+ − x−)
−
εµ
x+ − εµ
x−
2
|x1 − x|2
xµ + |x|2
(x1 − x)µ . (27)
Subham Dutta Chowdhury Conformal field theories and three point functions 17/51

18. The contribution to energy functional by the parity violating term I is given by,
ˆE(j)I =
g1
j (E)
g2
j (E)
, (28)
where,
g1
j (E) = d3
xeiEt
∞
−∞
dx−
1 lim
x+
1 →∞
x+
1 − x−
1
4
I,
g2
j (E) = jx(x)|jx(0) jy(x)|jy(0) . (29)
We note correlators are not time ordered. However, the energy functional must
be inserted between the operator creating the state and the one annihilating it.
This is achieved by assigning the operator to the left, a larger negative
imaginary part in time than the operators to the right i.e, t1 → t1 − i ,
t → t − 2i . Hence the light-cone coordinates change x±
1 → x±
1 − i ,
x±
→ x±
− 2i .
Subham Dutta Chowdhury Conformal field theories and three point functions 18/51

19. The calculation proceeds by taking first taking the limit x+
1 → ∞.
Integral over x−
1 is then performed by using a Schwinger parametrization.
The integrals performed in this manner give the same result as the analytic
continuation of even dimensional integrals.
The rest of the integrals are then best performed by integrating along the
spatial direction x followed by the light cone directions x±
.
The final result is
g1
j (E) = −
3pj
160
E2
π3
,
g2
j (E) = −
8
3
Eπ3
(c + e), (30)
where, c and e are defined in terms of nj
s and nj
f .
c =
3(2nj
f + nj
s)
256π3
, e =
3nj
s
256π3
. (31)
Subham Dutta Chowdhury Conformal field theories and three point functions 19/51

20. The complete energy functional matrix corresponding to charge excitations is
given by,
ˆE(j) =


E
4π
(1 − a2
2
) E
8π
αj
E
8π
αj
E
4π
(1 + a2
2
)

 , (32)
where
a2 =
2(3e − c)
(e + c)
= −
2(nj
f − nj
s)
(nj
f + nj
s)
,
αj =
3pjπ
32(c + e)
=
4π4
pj
(nj
f + nj
s)
. (33)
The diagonal contributions are due to the usual parity even part of the three
point function. Off diagonal elements are solely due to the parity violating part.
Positivity of energy flux implies,
a2
2 + α2
j ≤ 4. (34)
Subham Dutta Chowdhury Conformal field theories and three point functions 20/51

21. Energy matrix for stress tensor excitations
The three point function of the stress tensor is the starting point of this
calculation.
T(x)T(x1)T(0) =
µν
1 IT
µν,µ ν (x) σρ
2 IT
σρ,σ ρ (x1) αβ
3 tµ ν σ ρ
αβ
x6x6
1
+
pT
(P2
1 Q2
1 + 5P2
2 P2
3 )S1 + (P2
2 Q2
2 + 5P2
3 P2
1 )S2 + (P2
3 Q2
3 + 5P2
3 P2
1 )S3
|x − x1||x1|| − x|
,
(35)
where pT is the coefficient of the parity violating part.
The tensor structures in the first line correspond to the parity even part while
the parity violating contribution is due the structures in the second line.
Subham Dutta Chowdhury Conformal field theories and three point functions 21/51

22. Proceeding similarly we have the energy matrix due to the stress tensor
excitations
ˆE(T) =


E
4π
(1 − t4
4
) E
16π
αT
E
16π
αT
E
4π
(1 + t4
4
)

 , (36)
where,
t4 = −
4(30A + 90B − 240C)
3(10A − 2B − 16C)
= −
4(nT
f − nT
s )
nT
f + nT
s
,
αT =
pT
256
240π
5A − B − 8C
=
8π4
pT
3(nT
f + nT
s )
. (37)
The positivity of energy matrix then translates to
t2
4 + α2
T ≤ 16. (38)
Subham Dutta Chowdhury Conformal field theories and three point functions 22/51

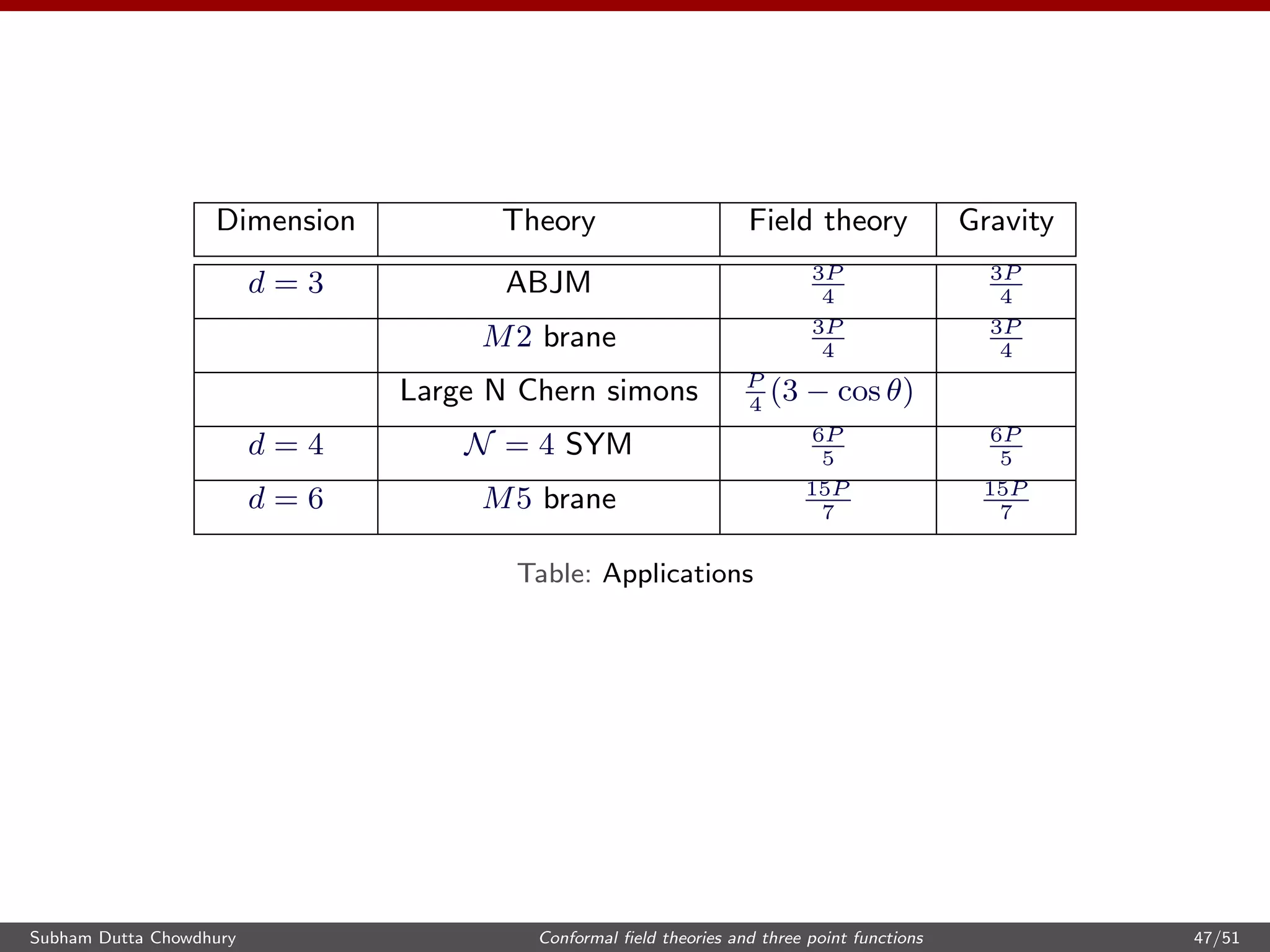
23. Large N Chern Simons theories
U(N) Chern Simons theory at level κ coupled to either fermions or bosons in
the fundamental representation are examples of conformal field theories which
violate parity. In the large N limit, these can be solved to all orders in the ’t
Hooft coupling
[Giombi et al, 2011]
[Aharony et al, 2011]
We consider U(N) Chern Simons theory at level κ coupled to fundamental
fermions.
The coefficients for the three point functions at the large N limit (planar limit)
are given by,
nT
s (f) = nj
s(f) = 2N
sin θ
θ
sin2 θ
2
, nT
f (f) = nj
f (f) = 2N
sin θ
θ
cos2 θ
2
,
pj(f) = α N
sin2
θ
θ
, pT (f) = αN
sin2
θ
θ
,
where the t ’Hooft coupling is related to θ by
θ =
πN
κ
. (39)
[Maldacena, Zhiboedov 2012]
Subham Dutta Chowdhury Conformal field theories and three point functions 23/51

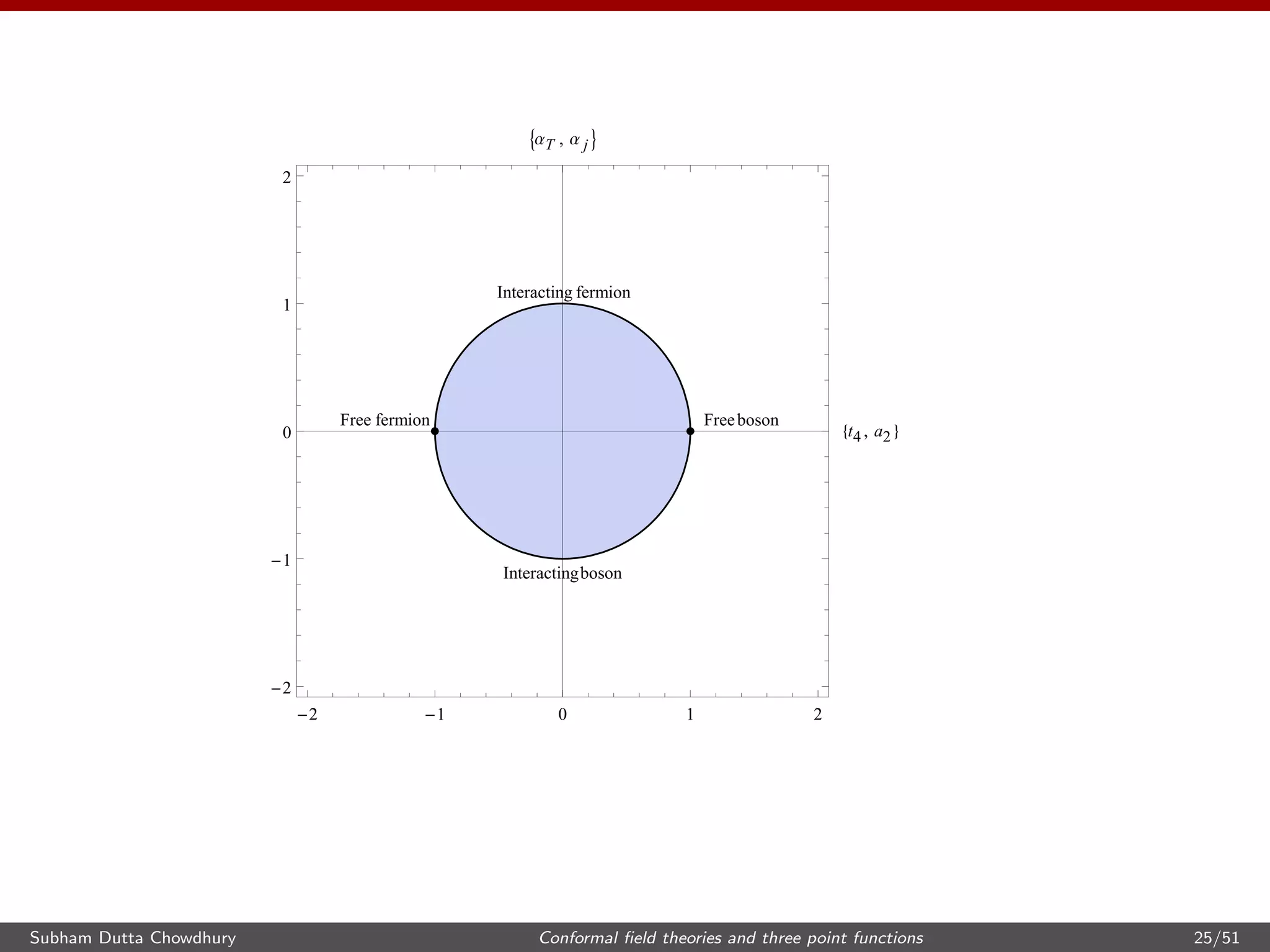
24. The numerical coefficients α, α can be determined by a one loop computation
in the theory with fundamental fermions.
[Giombi et al, 2011]
We repeat the analysis to precisely determine the factors α, α .
α =
3
π4
, α =
1
π4
. (40)
The parameters of the three point function take the form
a2 = −2 cos θ, αj = 2 sin θ, t4 = −4 cos θ, αT = 4 sin θ. (41)
Thus the Chern-Simons theories with a single fundamental boson or fermion
saturate the conformal collider bounds and they lie on the circles
a2
2 + α2
j = 4, t2
4 + α2
T = 16. (42)
The location of the theory on the circle is given by θ the t ’Hooft coupling.
Subham Dutta Chowdhury Conformal field theories and three point functions 24/51

25. 2 1 0 1 2
2
1
0
1
2
t4 , a2
ΑT , Α j
Free fermion Freeboson
Interacting fermion
Interactingboson
Subham Dutta Chowdhury Conformal field theories and three point functions 25/51

26. Sum Rules
The sum rule relates a weighted integral of the spectral density over frequencies
to one point functions of the theory
∞
−∞
dω
ωn
ρ(ω) ∝ One point functions ,
ρ(ω) = ImGR(ω), (43)
where GR(ω) is the retarded Green’s function at finite temperature.
The real time finite retarded correlators are difficult to obtain from lattice
calculations in QCD. However since one point functions are considerably easier
to obtain, this has led to systematic study of sum rules in QCD.
Sum rules provide important constraints on the spectral densities of any
quantum field theory.
Subham Dutta Chowdhury Conformal field theories and three point functions 26/51

27. We aim to compute sum rules for conformal field theories in d > 2. An
operator universal to CFTs is the stress tensor Tµν . We will look at the sum
rule for the retarded correlator,
GR(t, x) = iθ(t) [Txy(t, x), Txy(0)] .
(44)
at finite temperature and zero chemical potential
We assume that no other operators apart from the stress tensor gets
expectation values.
The Fourier transform of the retarded correlator is given by,
GR(ω, 0) = dd
xeiωt
GR(t, x) (45)
Subham Dutta Chowdhury Conformal field theories and three point functions 27/51

28. General Setup
The sum rules assume the analyticity and the well behaved behaviour of the
retarded correlator as ω → i∞,
1) GR(ω) is analytic in the upper half plane including the real axis.
2) limω→i∞ GR(ω) ∼ 1
|ω|m , m > 0
By Cauchy’s theorem,
GR(ω + i ) =
1
2πi
∞
−∞
dz
GR(z)
Z − ω − i
(46)
0 =
1
2πi
∞
−∞
dz
GR(z)
Z − ω + i
(47)
where the contour closes in a semi circle in the upper half plane.
From these two equations, we have,
G(0) = lim
→0+
∞
−∞
dω
π
ρ(ω)
ω − i
(48)
where, ρ(ω) = ImGR(ω)
Subham Dutta Chowdhury Conformal field theories and three point functions 28/51

29. Justifications for assumptions
The physical reason why the retarded correlator is analytic in the upper half
plane is causality. It is easy to see this from the inverse Fourier transform
GR(t) =
dω
2π
e−iωt
GR(ω). (49)
For t < 0 and only when GR(ω) is holomorphic, the contour can be closed in
the upper half plane resulting in GR(t < 0) = 0 which is a requirement for the
retarded correlator.
In order to examine the second assumption, we look at CFTs at finite
temperature and retarded correlators of the stress tensor.
Subham Dutta Chowdhury Conformal field theories and three point functions 29/51

30. At high frequencies the retarded correlator exhibits a divergent behaviour.
In order to understand this behavior in a precise manner, we analytically
continue GR(ω) into the upper half plane
GR(i2πnT) = GE(2πnT). (50)
Here GE is the Euclidean time ordered correlator and 2πnT is the Matsubara
frequency.
Consider the Euclidean correlator in position space. For time intervals
δt β = 1
T
, the operator product expansion (OPE) of the stress tensor offer a
good asymptotic expansion. Therefore for ω T, we can replace the
Euclidean correlator by its OPE. This allows us to obtain the asymptotic
behaviour of the GR(iω) as ω → ∞.
[Romatschke, Son, 2009]
Subham Dutta Chowdhury Conformal field theories and three point functions 30/51

31. OPE of the stress tensor in the Euclidean two point function is given by,
Txy(s)Txy(0) ∼ CT
Ixy,xy(s)
s2d
+ ˆAxyxyαβ(s) Tαβ(0) + · · · (51)
where expectation value has been taken over thermal states.
The stress tensor in d dimensions has scaling dimensions d. By dimensional
analysis, the tensor structure Iµνρσ is dimensionless, while the ˆAµνρσ scales like
1/sd
.
Their fourier transforms scale as
dd
xeiωt
CT
Ixy,xy(x)
|x2d|
≡ I ∼ ωd
log
ω
Λ
,
∞
−∞
dd
xeiωt ˆAxyxyαβ(x) Tαβ ≡ J ∼ ω0
ˆaαβ
Tαβ . (52)
where λ is a cut off in the integration.
We assume that there is no chemical potential turned on and no other operator
except stress tensor gets expectation value.
Subham Dutta Chowdhury Conformal field theories and three point functions 31/51

32. We obtain
lim
ω→∞
GR(iω) ∼ ωd
f
ω
λ
+ ω0
T + O
1
ω
∼ ωd
f
ω
λ
+ J (53)
We have a divergent piece along with a finite term. The assumption about well
behaved behaviour of the retarded green’s function breaks down.
Subham Dutta Chowdhury Conformal field theories and three point functions 32/51

33. The divergent piece is identical to the Fourier transform of the retarded Greens
function at zero temperature.
To remove the divergent term we consider the following regularized Green’s
function
δGR(ω) = GR(ω)|T − GR(ω)|T =0. (54)
To remove the finite parts, we consider,
δGR(ω) = GR(ω)|T − GR(ω)|T =0 − J . (55)
We have constructed a regularized green’s function which is analytic in the
upper half plane and is well behaved as ω → i∞.
Subham Dutta Chowdhury Conformal field theories and three point functions 33/51

34. The sum rule then becomes,
lim
→0+
1
π
∞
−∞
δρ(ω)dω
ω − i
= δGR(0),
GR(t, x) = iθ(t)[Txy(t, x), Txy(0)],
(56)
where δρ(ω) is the difference of spectral densities
δρ(ω) = Im(GR(0)|T − GR(0)|T =0)
= ρ(ω) − ρ(ω)T =0,
δGR(0) = GR(0)|T − GR(0)|T =0 − J . (57)
Note that the finite term does not feature in the difference of spectral densities.
It will turn out to be real and will not contribute to the spectral densities.
The first term is obtained from the hydrodynamic behaviour of the theory while
high frequency behaviour is captured by the OPE.
Subham Dutta Chowdhury Conformal field theories and three point functions 34/51

35. Shear sum rule d ≥ 3
The OPE of the Euclidean two point function in general dimensions is well
studied.
The tensor structures in OPE are as follows,
Txy(s)Txy(0) ∼ CT
Ixy,xy(s)
s2d
+ ˆAxyxyαβ(s) Tαβ(0) + · · · (58)
[Osborn, Petkou 1993]
where CT is the normalization of the two point function of the stress tensor.
The coefficients are determined in terms of the parameters of the three point
function of the stress tensor (a, b, c)
Note that for d = 3, there is no additional contribution from the parity odd
structure, for the shear channel.
Subham Dutta Chowdhury Conformal field theories and three point functions 35/51

36. Fourier Transform
In order to examine the high frequency behaviour, we look at the OPE in a bit
more detail.
ˆAµνρσαβCT =
(d − 2)
d + 2
(4a + 2b − c)H1
αβµνρσ(s) +
1
d
(da + b − c)H2
αβµνρσ(s)
−
d(d − 2)a − (d − 2)b − 2c
d(d + 2)
(H2
µνρσαβ(s) + H2
ρσµναβ(s))
+
2da + 2b − c
d(d − 2)
H3
αβµνρσ(s)
−
2(d − 2)a − b − c
d(d − 2)
H4
αβµνρσ(s) −
2((d − 2)a − c)
d(d − 2)
2H3
µνρσαβ(s)
+
((d − 2)(2a + b) − dc)
d(d2 − 4)
(H4
µνρσαβ + H4
ρσµναβ)(s)
+(Ch5
µνρσαβ + D(δµν h3
ρσαβ + δρσh3
µναβ))Sdδd
(s).
(59)
where,
CT =
8π
d
2
Γ(d
2
)
(d − 2)(d + 3)a − 2b − (d + 1)c
d(d + 2)
,
C =
(d − 2)(2a + b) − dc
d(d + 2)
, Sd =
2π
d
2
Γ(d
2
)
Subham Dutta Chowdhury Conformal field theories and three point functions 36/51

37. We fourier transform all the terms in the OPE and we obtain,
J = A + B
A =
(1 − d)P(a(d(d + 4) − 4) + d(2b − c))
2 (−a (d2 + d − 6) + 2b + cd + c)
B =
((2a + b)(−2 + d) − cd)P
−2b − c(1 + d) + a (−6 + d + d2)
,
(60)
A is the contribution from tensor structures and B is the contribution from the
contact term.
The contribution A, due the tensor structures without the contact terms, is
proportional to the Hofman-Maldacena coefficient in general d dimensions.
[Meyers, Sinha 2009]
Subham Dutta Chowdhury Conformal field theories and three point functions 37/51

38. We are in a position to state our sum rule.
δGR(ω) = GR(ω)|T − GR(ω)|T =0 − (A + B). (61)
RHS of the sum rule is given by
δGR(0) =
2c + d(c + 2bd − cd) + a 8 + d −6 + d + d2
P
2(2b + c + cd) − 2a (−6 + d + d2)
(62)
where,
GR(0)|T = P, GR(0)|T =0 = 0
P = Tii i = t (63)
Subham Dutta Chowdhury Conformal field theories and three point functions 38/51

39. Holography Check 1
The coefficients a, b, c have been evaluated in AdSd+1 by evaluating the 3
point function of the stress tensor holographically.
[Arutyunov, Frolov 1999]
a = −
d4
π−d
Γ[d]
4(−1 + d)3
,
b = −
d 1 + (−3 + d)d2
π−d
Γ(1 + d)
4(−1 + d)3
,
c =
d3
(1 − 2(−1 + d)d)π−d
Γ(d)
4(−1 + d)3
.
(64)
Evaluating A and B, we have,
A = −
d
2(d + 1)
, B = P (65)
Subham Dutta Chowdhury Conformal field theories and three point functions 39/51

40. We now evaluate the sum rule,
δGR(0) =
d
2(d + 1)
lim
→0+
1
π
∞
−∞
δρ(ω)dω
ω − i
=
d
2(d + 1)
(66)
For d = 4 this becomes
lim
→0+
1
π
∞
−∞
δρ(ω)dω
ω − i
=
2
5
(67)
[Son, Romatschke 2009]
Subham Dutta Chowdhury Conformal field theories and three point functions 40/51

41. Holography Check 2
An alternate way of deriving the sum rule is to directly study the Green’s
functions in AdSd+1 black hole background and obtain the high frequency
behaviour.
The shear sum rule was first studied holographically in the context of AdS5.
[Son, Romatschke 2009]
This method of directly evaluating green’s function was generalised to arbitrary
dimensions by Herzog et al. The analyticity of the Green’s functions in the
upper half plane is obtained by studying the differential equations.
[Gulotta, Herzog, Kaminski 2010]
Modifications to the shear sum rule for retarded correlators of stress tensor as
well as currents in presence of chemical potential have also been studied.
[Jain, Thakur, David 2011],
[Thakur, David 2012],
Subham Dutta Chowdhury Conformal field theories and three point functions 41/51

42. Using Cauchy’s theorem then one gets for general dimensions,
1
π
∞
−∞
dω
ω
[ρ(ω) − ρT =0(ω)] =
d
2(d + 1)
(68)
This is a consistency check for shear sum rule of conformal field theories in
arbitrary dimensions.
[Gulotta, Herzog, Kaminski 2010]
From this we come to the conclusion that, the parameters of the three point
function of stress tensor of any conformal field theory with a two derivative
gravity dual must satisfy the following constraint.
2c + d(c + 2bd − cd) + a 8 + d −6 + d + d2
2(2b + c + cd) − 2a (−6 + d + d2)
=
d(d − 1)
2(d + 1)
(69)
Subham Dutta Chowdhury Conformal field theories and three point functions 42/51

43. Applications in d = 4
Positivity of energy flux/ Causality constraints lead to certain bounds on the
parameters of the three point function of the stress tensor.
[Hofman, Maldacena 2008]
−
t2
3
−
2t4
15
+ 1 ≥ 0
2 −
t2
3
−
2t4
15
+ 1 + t2 ≥ 0
3
2
−
t2
3
−
2t4
15
+ 1 + t2 + t4 ≥ 0 (70)
We can rewrite the general sum rule for d = 4 in terms of collider variables to
get
δGR(0) = (
6
5
−
t2
6
−
2t4
75
)P (71)
The causality bounds then translate to the following bounds on the sum rule
P
2
≤ δGR(0) ≤ 2P (72)
The lower bound is saturated for theories with only free fermions, while the
upper bound is saturated for theories with only free bosons.
Subham Dutta Chowdhury Conformal field theories and three point functions 43/51

44. There is a similar parametrization of the parameters of the three point
functions, in d dimensions, in terms of t2, t4.
[Buchel et al 2009]
The general expression for sum rule can be expressed in terms of these
parameters.
δGR(0) =
(−1 + d)d
2(1 + d)
+
(3 − d)t2
2(−1 + d)
+
2 + 3d − d2
t4
(−1 + d)(1 + d)2
P (73)
The Causality constraints in terms of these variables is given by
[Camanho, Edelstein 2009]
1 −
1
d − 1
t2 −
2
(d + 1)(d − 1)
t4 ≥ 0, (74)
1 −
1
d − 1
t2 −
2
(d + 1)(d − 1)
t4 +
1
2
t2 ≥ 0,
1 −
1
d − 1
t2 −
2
(d + 1)(d − 1)
t4 +
d − 2
d − 1
(t2 + t4) ≥ 0.
Subham Dutta Chowdhury Conformal field theories and three point functions 44/51

45. The causality constraints imply the following bounds on shear sum rule for any
conformal field theory in d dimensions.
1
2
P ≤ δGR(0) ≤
d
2
P. (75)
For d = 3, the causality constraints are (ignoring any parity odd structures that
might appear in the three point function)
1 −
t4
4
≥ 0
1 +
t4
4
≥ 0 (76)
The bounds on the sum rule is then,
1
2
P ≤ δGd=3
R (0) ≤ P. (77)
Subham Dutta Chowdhury Conformal field theories and three point functions 45/51

46. For free N = 4 super Yang-Mills, the parameters a, b and c take the values,
a = −
16
9π6
(N2
c − 1), b = −
17
9π6
(N2
c − 1), c = −
92
9π6
(N2
c − 1).
Substituting these values into the sum rule for d = 4 we get,
δGR(0) =
2
5
Note that this is exactly the same result from our holographic calculation. We
see that the sum rule has not been renormalized.
We also note that sum rules for theories with two derivative gravitational dual
is consistent with the following observation,
t2 = 0, t4 = 0 (78)
Subham Dutta Chowdhury Conformal field theories and three point functions 46/51

47. Dimension Theory Field theory Gravity
d = 3 ABJM 3P
4
3P
4
M2 brane 3P
4
3P
4
Large N Chern simons P
4
(3 − cos θ)
d = 4 N = 4 SYM 6P
5
6P
5
d = 6 M5 brane 15P
7
15P
7
Table: Applications
Subham Dutta Chowdhury Conformal field theories and three point functions 47/51

48. Sum rules in higher derivative gravity
We can perform similar analysis for gauss bonnet gravity theories in d = 5
(fourth order in derivatives).
The holographic sum rule, obtained by solving a modified minimally coupled
scalar equation, becomes
δG(0) =
6
5
+ 2 1 −
1
√
1 − 4λGB
P (79)
This is consistent with the sum rule that we have derived, with the following
values for t2 and t4
t4 = 0, t2 =
24f∞λGB
1 − 2f∞λGB
(80)
where,
f∞ =
1 −
√
1 − 4λGB
2λGB
(81)
[Buchel et al 2009]
Can be generalised to a generic higher derivative theory (fourth order in
derivatives) in arbitrary dimensions. This will serve as a non trivial check of the
coefficient of t2 in our sum rule.
Subham Dutta Chowdhury Conformal field theories and three point functions 48/51

49. Conclusions
We have obtained constraints on the three-point functions jjT , TTT that
apply to all (both parity-even and parity-odd) conformal field theories in d = 3
by imposing the condition that energy observed at the conformal collider be
positive.
In particular, if the parameters which determine the TTT correlation function
be t4 and αT , where αT is the parity-violating contribution and the
parameters which determine jjT correlation function be a2, and αJ , where
αJ is the parity-violating contribution we have the following bounds
a2
2 + α2
j ≤ 4, t2
4 + α2
T ≤ 16 (82)
We have explicitly shown that for large N, U(N) Chern-Simons theories with a
single fundamental fermion or a fundamental boson, these parameters lie on
the bounding circles of these disc.
We have derived the sum rule corresponding to the shear channel of stress
tensor correlator for any conformal field theory in d dimensions.
lim
→0+
1
π
∞
−∞
δρ(ω)dω
ω − i
=
(−1 + d)d
2(1 + d)
+
(3 − d)t2
2(−1 + d)
+
2 + 3d − d2
t4
(−1 + d)(1 + d)2
P,
where ρ(ω) is the spectral density corresponding to the retarded correlators.
Subham Dutta Chowdhury Conformal field theories and three point functions 49/51

50. Causality constrains the shear sum rule to lie within specific bounds.
1
2
P ≤ δGR(0) ≤
d
2
P. (83)
We see that for d = 4, the constraint on a, b and c from equality of the central
charges and the sum rule, can be expressed as
t2 = t4 = 0
(84)
It will be interesting to generalise conformal collider experiment to excitations
created by higher spin currents.
Note that the other Hofman-Maldacena coefficients appear in the high
frequency behaviour of other channels. It might be worthwhile setting up the
sum rule for the other channels and explore them holographically.
Moreover, for d = 3, the sum rules in the other channels will be affected by the
parity violating terms in the three point functions. It might be enlightening to
study these sum rules and find the bounds on them.
Subham Dutta Chowdhury Conformal field theories and three point functions 50/51

51. Thank you.
Subham Dutta Chowdhury Conformal field theories and three point functions 51/51