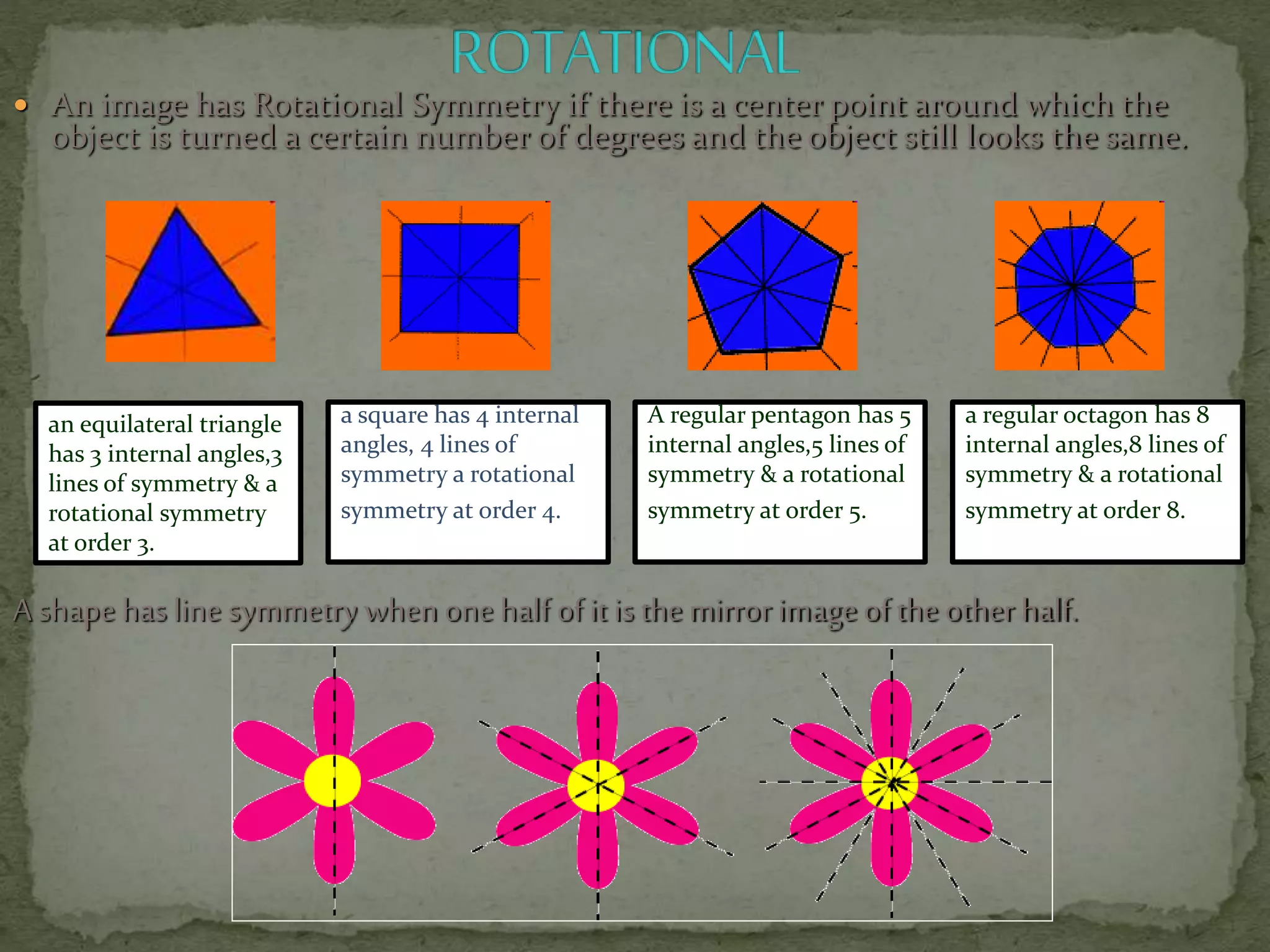
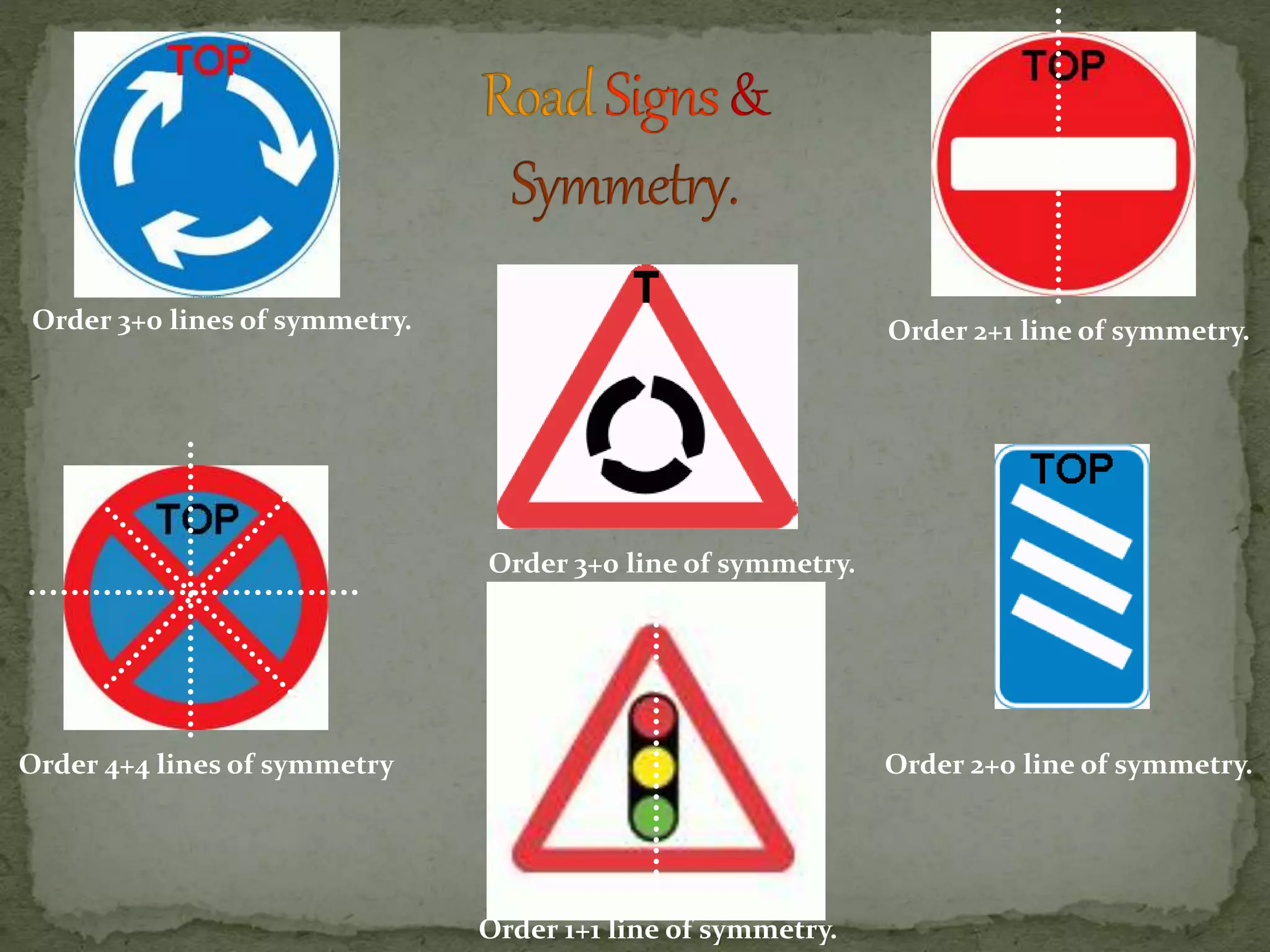
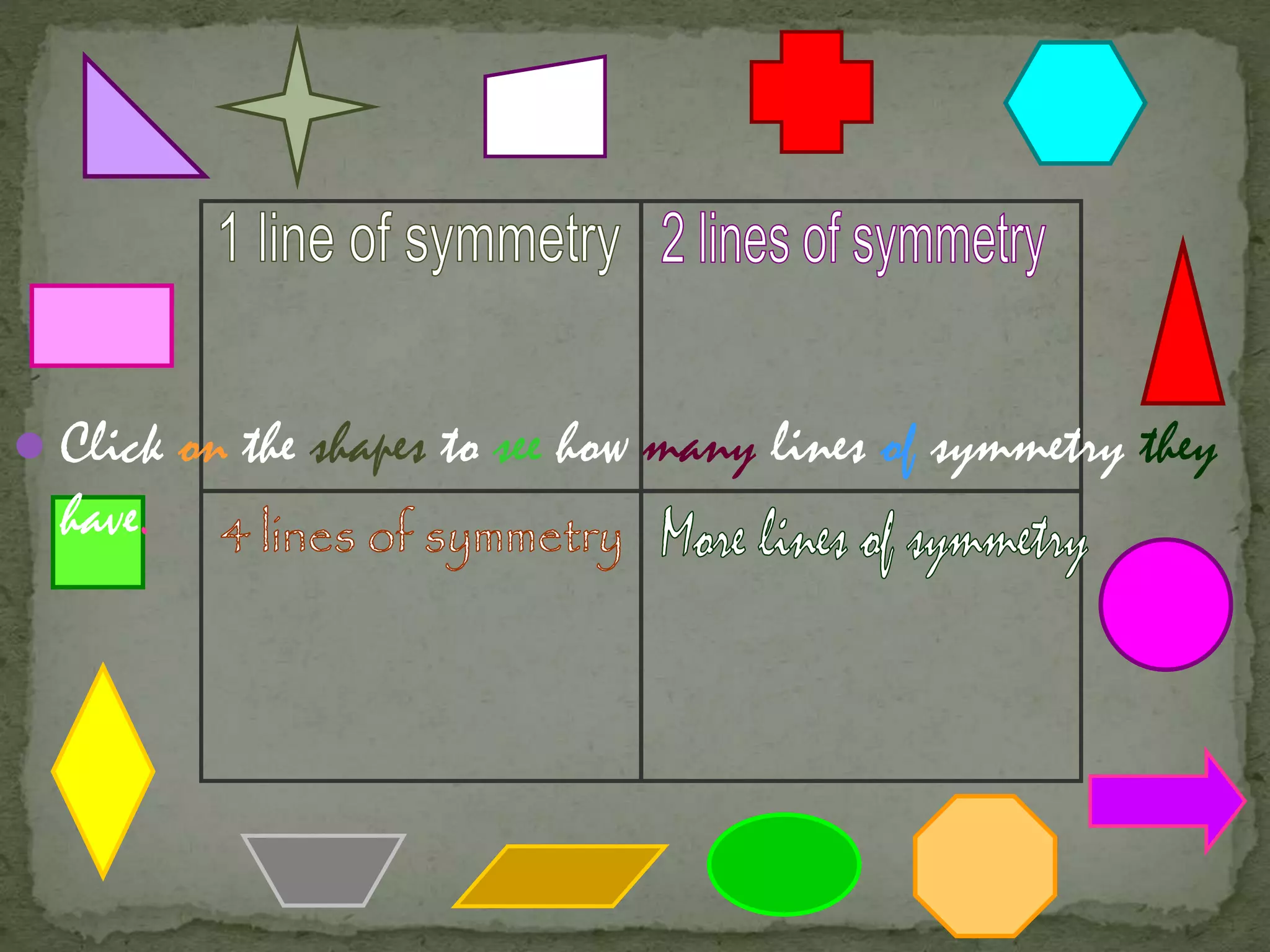
This document discusses different types of symmetry, including line symmetry and rotational symmetry. It provides examples of line symmetry in letters of the alphabet and examples of rotational symmetry in shapes like triangles, squares, and pentagons. It also discusses symmetry in architecture, flags, and natural phenomena. Symmetry is a fundamental organizing principle in nature and art that involves preserving certain properties when an object is transformed in some way.

3.  Fundamental organizing principle in nature and art.
 Preserves distances, angles, sizes and shapes.

4.  Line symmetry
 line that divides
a figure into two
halves that are
mirror images of
each other

5.  An attribute of a
shape
 exact reflection of form
on opposite sides of a
dividing line
 Line symmetry
 line that divides a figure
into two halves that are
mirror images of each
other

6.  Sort the letters of the alphabet into groups according
to their symmetries
 Divide letters into two categories:
 symmetrical
 not symmetrical

7. A B C D E
H I M O
T U V W X Y
There are some letters which
do not have any line of
symmetry.
F G J K L N P Q S Z

8. Letters and Rotational
N
S
X
I
O
Z
rotational
symmetry
at order 1
rotational
symmetry at
order 2
rotational
symmetry at
order 2
rotational
symmetry at
order 2
rotational
symmetry at order
2
rotational
symmetry at
order 2
rotational
symmetry
at order 1
Symmetry.

9.  An image has Rotational Symmetry if there is a center point around which the
object is turned a certain number of degrees and the object still looks the same.
an equilateral triangle
has 3 internal angles,3
lines of symmetry & a
rotational symmetry
at order 3.
a square has 4 internal
angles, 4 lines of
symmetry a rotational
symmetry at order 4.
A regular pentagon has 5
internal angles,5 lines of
symmetry & a rotational
symmetry at order 5.
a regular octagon has 8
internal angles,8 lines of
symmetry & a rotational
symmetry at order 8.
A shape has line symmetry when one half of it is the mirror image of the other half.

10. Common Errors
 There are some examples of shapes that are tricky when
considering symmetry. A typical parallelogram actually cannot
be folded in half even though it appears to have two 'equal
halves'.
• We can see both kinds of symmetry around us; rotational as
well as line symmetry.

11. Order 3+0 lines of symmetry. Order 2+1 line of symmetry.
Order 4+4 lines of symmetry
Order 3+0 line of symmetry.
Order 2+0 line of symmetry.
Order 1+1 line of symmetry.

12. Symmetry exists in
architecture all around
the world.
One of the best known
examples of this is the
Taj Mahal.
If an object is reflected in water many people believe
the image has line symmetry.
But is it really a 'mirror image'? Is it
really symmetrical?
What are your thoughts?
The image can be rotational
symmetry.

13. Japan Indonesia
Micronesia United Nations Aboriginal Flag of Australia
Finland
Canada British

14. Rotational symmetry-yes(
2)
Rotational symmetry-yes(
2)
Rotational symmetry-yes(
1)
Rotational symmetry-yes(
1)
Rotational symmetry-yes(
1)
Rotational symmetry-yes(
2)
Rotational symmetry-yes(
1)
Rotational symmetry-yes(
1)

15.  Click on the shapes to see how many lines of symmetry they
have.