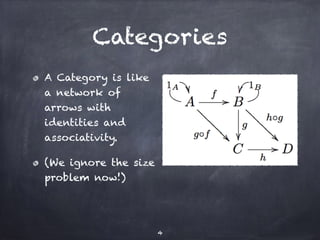
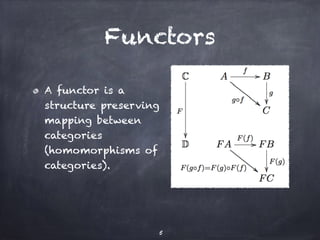
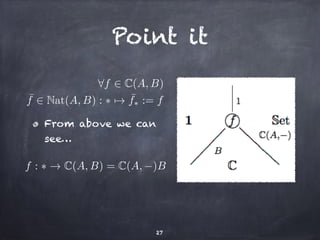
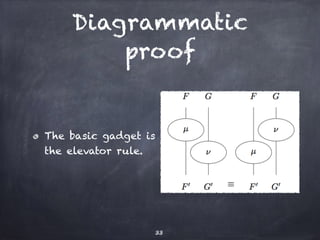
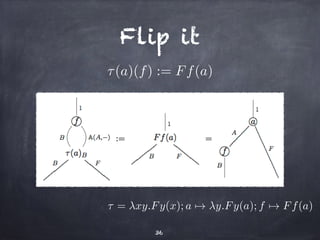
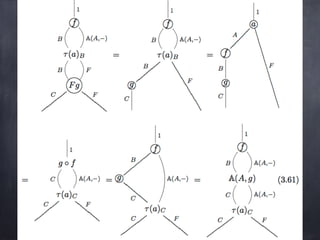
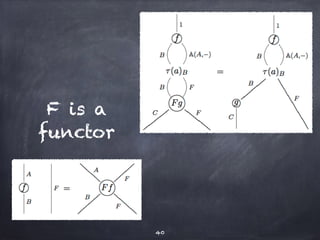
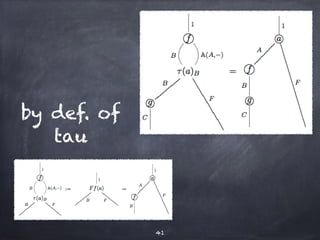
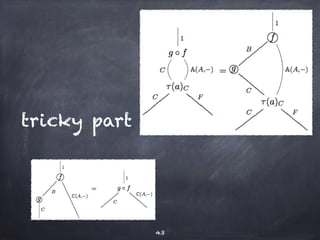
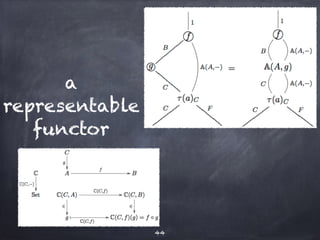
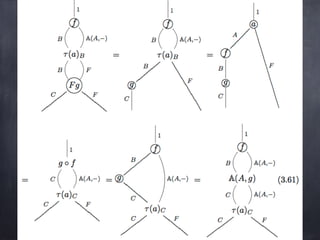
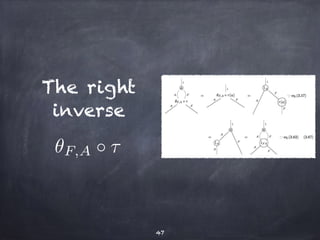
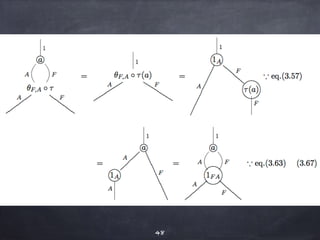
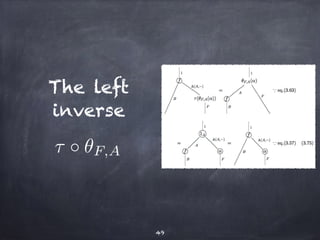
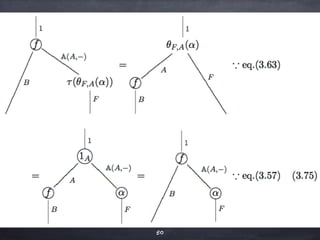
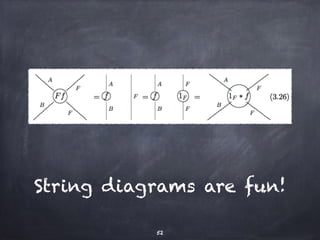
The document discusses the Yoneda lemma within the context of category theory, emphasizing categories, functors, and natural transformations, using string diagrams for diagrammatic proofs. It covers foundational concepts, examples, and various types of categories, illustrating complex ideas through visual representations and proofs. References to key literature and tools in categorical algebra are also included throughout the document.

1. The Yoneda lemma
and
String diagrams
Ray D. Sameshima
total 54 pages
1

2. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
2

3. References
Handbook of Categorical Algebra (F.
Borceux)
The Joy of String Diagrams (P. L.
Curien)
Category theory (P. L. Curien)
(in progress) Cat (R. D. Sameshima)
3

4. Categories
A Category is like
a network of
arrows with
identities and
associativity.
(We ignore the size
problem now!)
4

5. Functors
A functor is a
structure preserving
mapping between
categories
(homomorphisms of
categories).
5

6. Natural
transformations
A homotopy of categories.
6

7. Natural
transformations
A natural transformation consists of a
class (family, set, or collection) of
arrows.
7
s.t.

8. Natural
transformations
A natural transformation consists of a
class (family, set, or collection) of
arrows.
7
s.t.

9. Natural
transformations
We call this commutativity the naturality
of the natural transformations.
8

10. Natural
transformations
We call this commutativity the naturality
of the natural transformations.
8

11. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
9

12. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
9
✔

13. Examples
0
1
A category of sets and mappings
A class change method
Representable functors
Natural transformations
10

14. An empty category
The empty category: No object and no arrow.
11

15. A singleton
category
Discrete categories:
objects with
identities.
E.g., the singleton
(one-point set) can
be seen as a
discrete category 1.
12

16. Set
The mappings
satisfy the
associativity law.
!
The identities are
identity mappings.
13
f : A ! B; a7! f(a)
g : B ! C; b7! g(b)
h : C ! D; c7! h(c)
h (g f)(a) = h(g(f(a))) = (h g) f(a)
1A : A ! A; a7! a

17. A class change
method
A class change
method: we can
always view an
arbitrary arrow as
a natural
transformation.
14
8f 2 C(A,B)
) 9 ¯ f 2 Nat( ¯ A, ¯B
)
where ¯ A, ¯B
2 Func(1,C)

18. Func(1,C)
This is just pointing mappings of
both objects and arrows in the
category that we consider.
¯ C 2 Func(1,C)
¯ C(⇤) := C 2 |C|
¯ C(1⇤) := 1C
So we can identify all objects as functors
from 1 to the category.
15

19. Nat(A,B 2 Func(1,C))
Under the
identifications, the
arrow in the
category can be
seen as the natural
transformation
between the objects.
16
8f 2 C(A,B)
¯ f 2 Nat(A,B) : ⇤7! ¯ f⇤ := f
This is, I call, a class change method.

20. Representable
functors
The functor
represented by
the object C.
17
C(C,−) 2 Func(C, Set)

21. C(C,−) 2 Func(C, Set)
Now we ignore the size problems but…
18

22. ↵ 2 Nat(C(C,−), F)
By definition
19
8B,C 2 |C|
↵C # C(A, g) = Fg # ↵B
8f 2 C(A,B)
↵C # C(A, g)(f) = Fg # ↵B(f)

23. Let me see
Now we get all gadgets for the
Yoneda lemma.
20

24. Yoneda lemma
A milestone of category theory.
21

25. Yoneda lemma
A milestone of category theory.
21

26. An equation based
proof
Basically, I traces
the proof in this
handbook -.
See my notes.
22

27. So many commutative
diagrams
Diagram chasing
are routine tasks in
the category theory.
23

28. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
24
✔

29. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
24
✔
✔

30. String diagrams
Flipping the diagrams!
25

31. String diagrams
Two categories, two
functors(objects),
and a n.t. (an
arrow.)
26
A
f!
B

32. Point it
8f 2 C(A,B)
¯ f 2 Nat(A,B) : ⇤7! ¯ f⇤ := f
From above we can
see…
f : ⇤ ! C(A,B) = C(A,−)B
27

33. Compositions
These are good examples of vertical
compositions.
28

34. Compositions
These are good examples of horizontal
compositions.
29

35. Basically, that’s all.
30

36. No Standard
Committees
… Enjoy!
Category Theory Using String Diagrams
31
(Dan Marsden)

37. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
32
✔
✔

38. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
32
✔
✔
✔

39. Diagrammatic
proof
The basic gadget is
the elevator rule.
33

40. Yoneda lemma
A milestone of category theory.
34

41. Yoneda lemma
A milestone of category theory.
34

42. Choose wisely
✓F,A(↵) := ↵A(1A)
35

43. Flip it
⌧ (a)(f) := Ff(a)
⌧ = xy.Fy(x); a7! y.Fy(a); f7! Ff(a)
36

44. Naturality
of tau
The Adventure of the
Dancing Men
37

45. 38

46. Step by step
39

47. F is a
functor
40

48. by def. of
tau
41

49. a composition
and the def.
of tau for gf
42

50. tricky part
43

51. a
representable
functor
44

52. 45

53. We have
proved the
naturality of
tau:
46
⌧ (a) 2 Nat (A(A,−), F)

54. The right
inverse
47
✓F,A ⌧

55. 48

56. The left
inverse
49
⌧ ✓F,A

57. 50

58. Finally, we have
proved that theta and
tau are the inverse
pair.
51
✓F,A ⌧ = 1FA
⌧ ✓F,A = 1Nat(A(A,),F )

59. String diagrams are fun!
52

60. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
53
✔
✔
✔

61. Outlines
Category theory (categories, functors,
and natural transformations)
Examples
String diagrams
Diagrammatic proof Yoneda lemma
and more…
53
✔
✔
✔
✔

62. Thank you!
54

63. 55

64. Godement products
and elevator rules
Commutativity and elevator rules
56