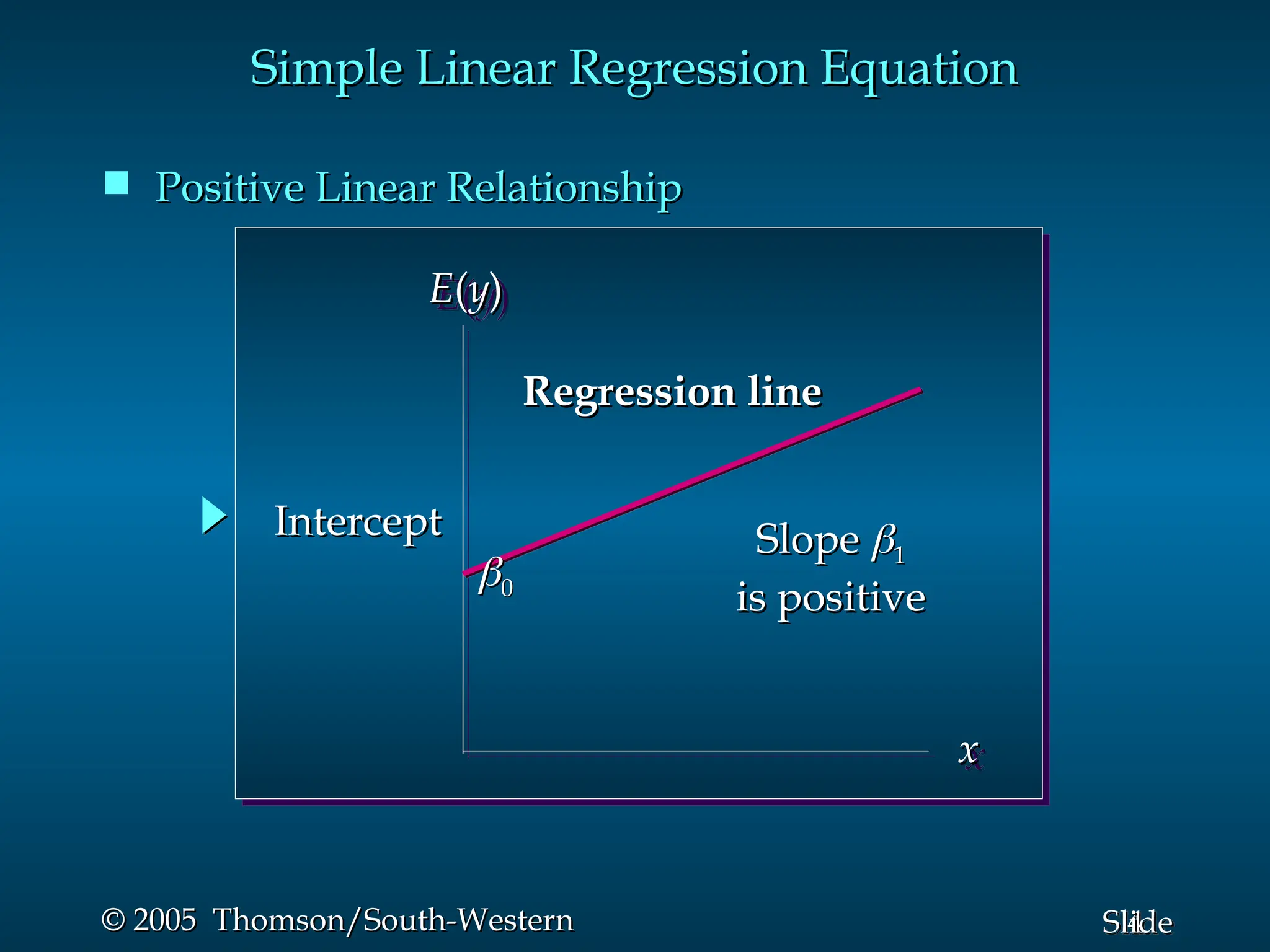
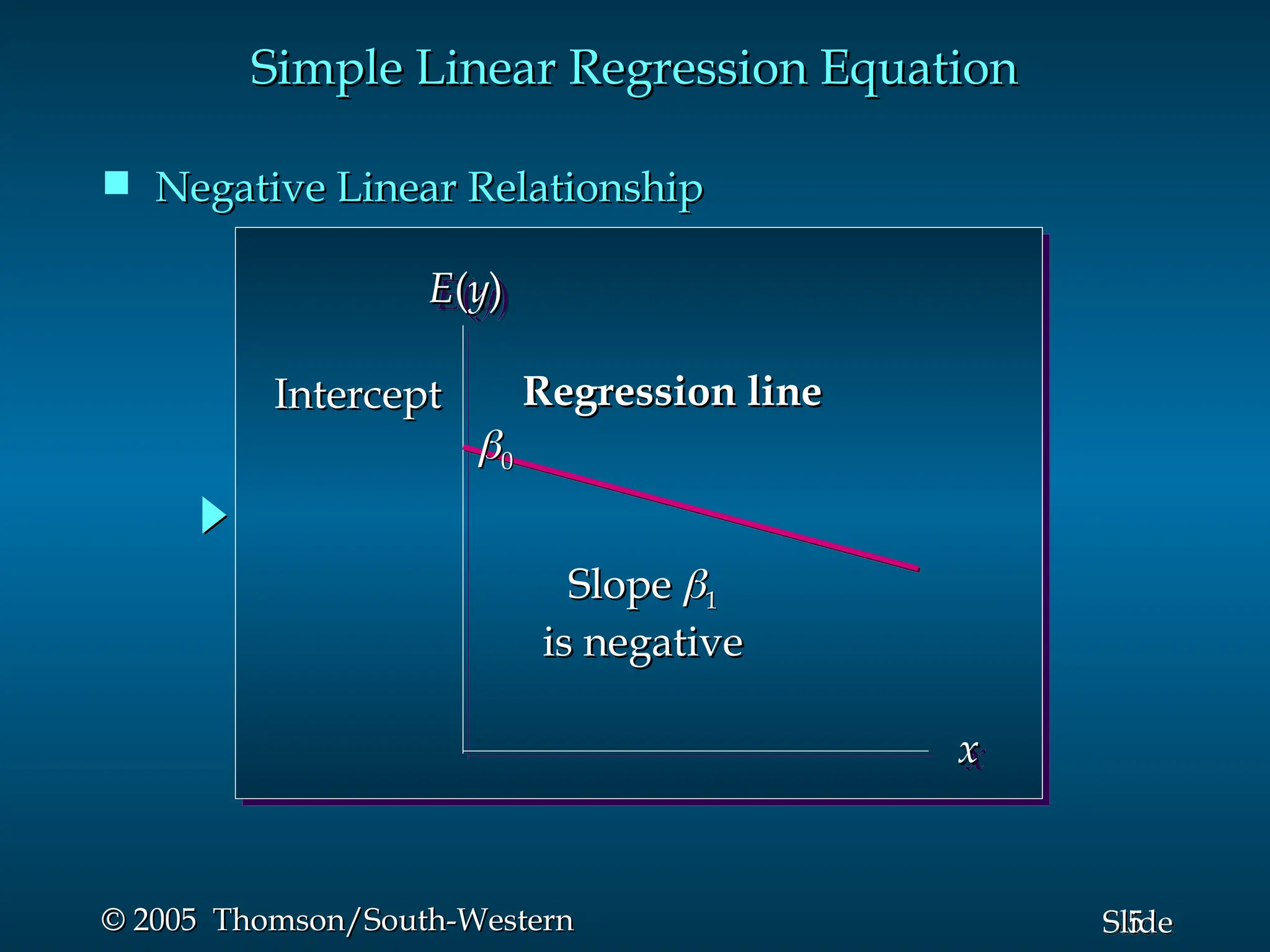
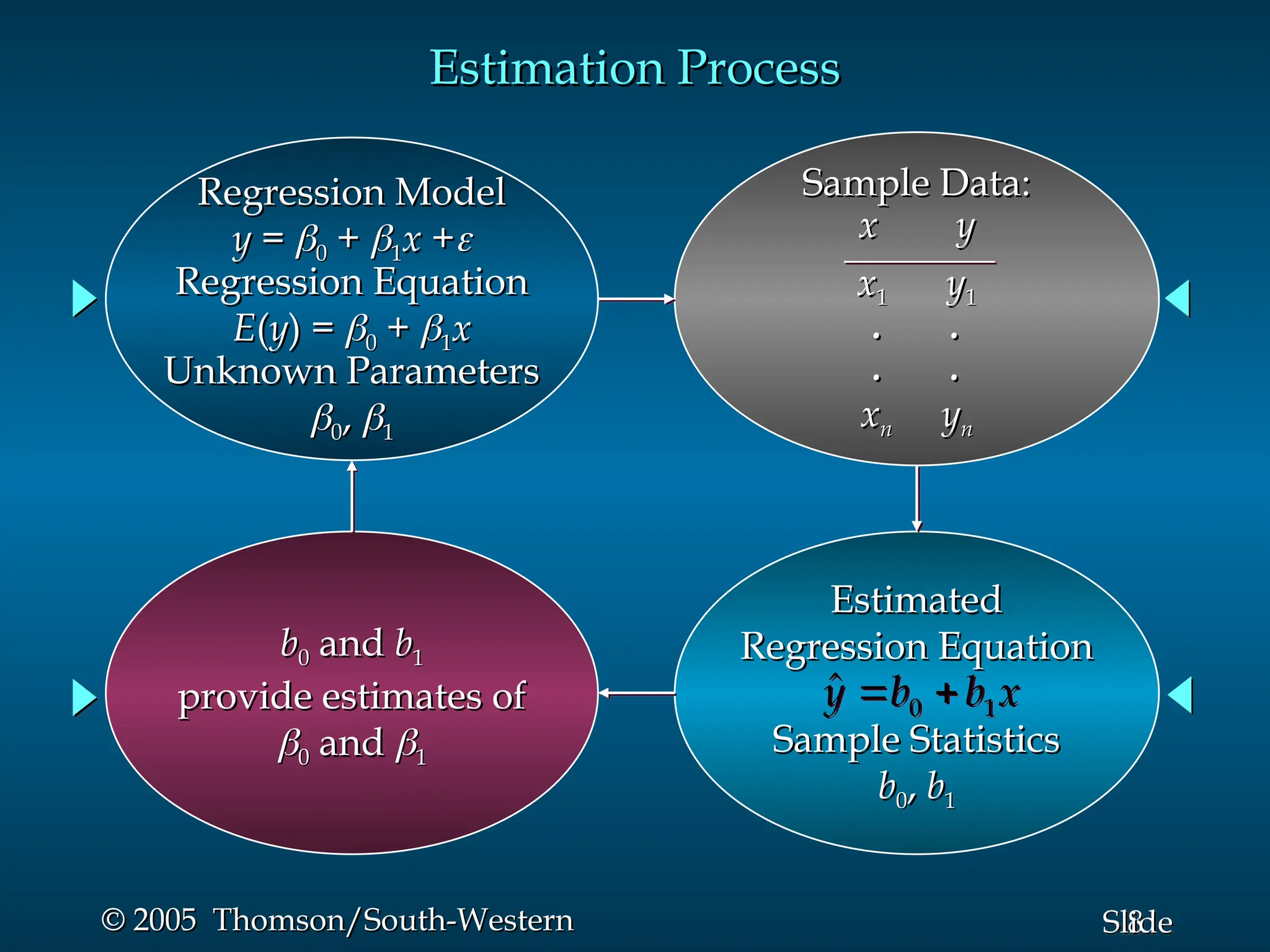
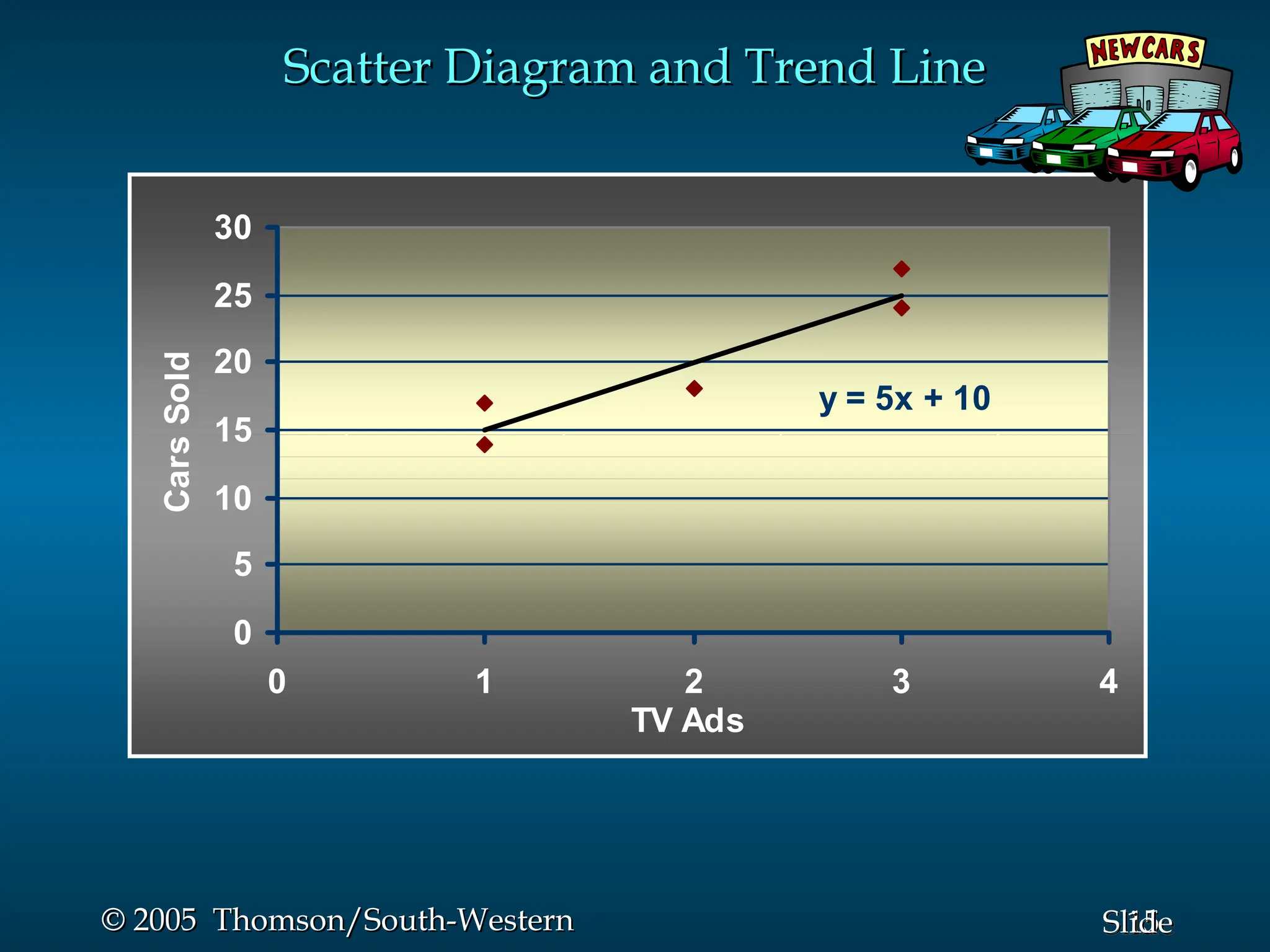
This document provides an overview of simple linear regression, covering its model, the least squares method, the coefficient of determination, and the significance testing for regression relationships. It includes details about the regression equation, its components, estimation process, and assumptions about errors. An example involving Reed Auto sales illustrates the application of these concepts with accompanying formulae, calculations, and results.