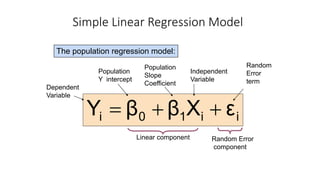
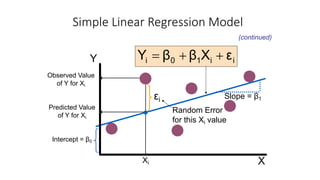
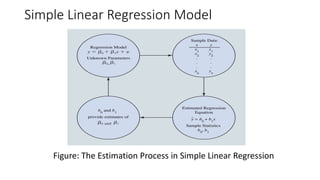
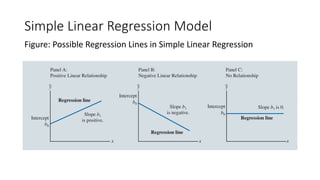
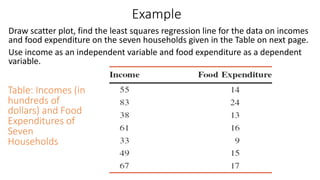
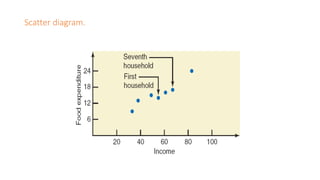
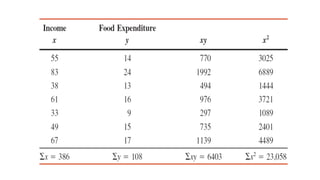
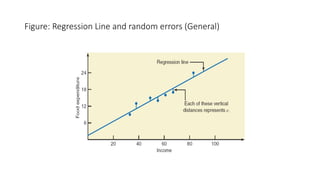
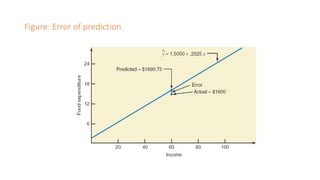
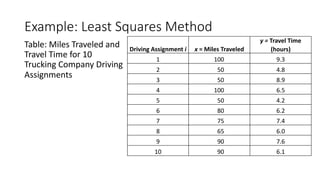
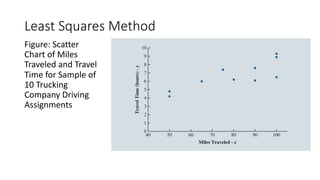
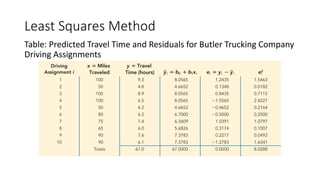
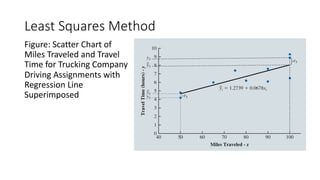
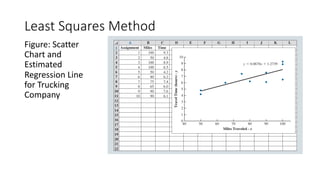
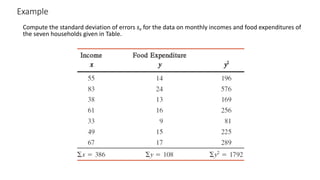
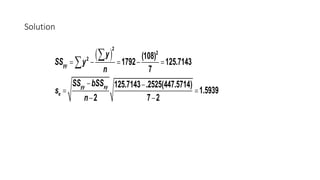
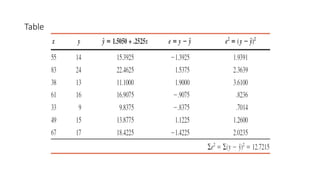
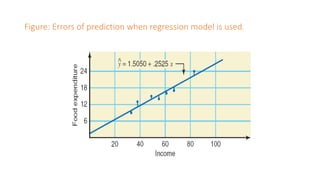
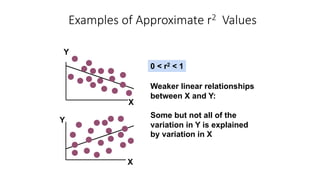
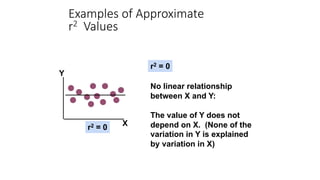
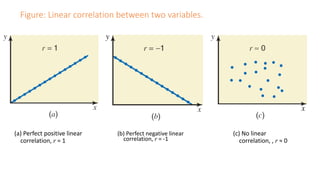
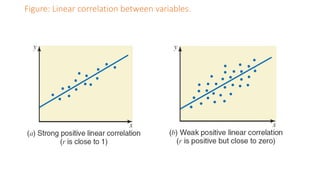
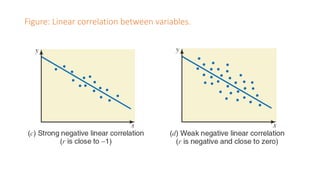
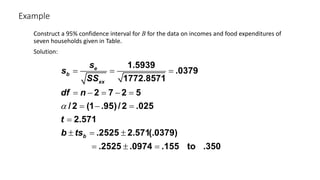
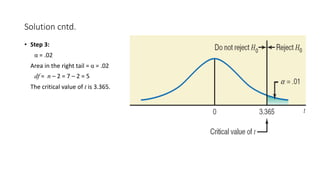
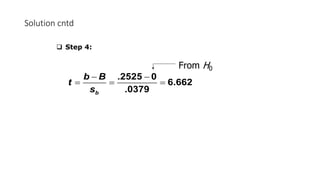
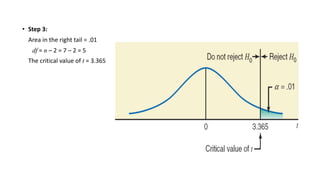
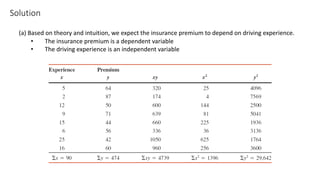
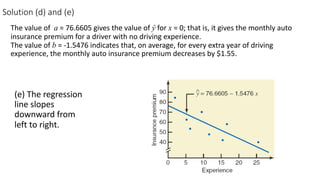
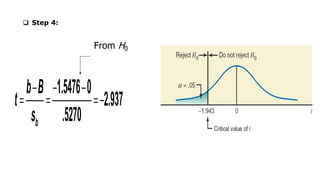
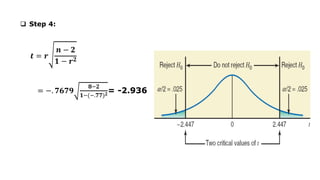
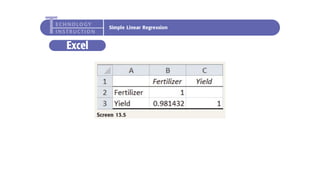
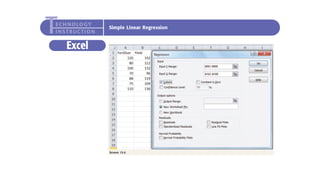
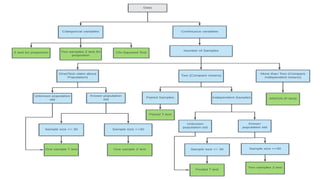
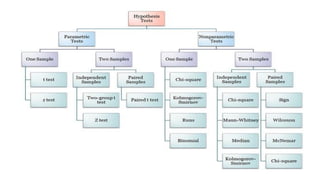
The document outlines key concepts in correlation and regression analysis, focusing on how these statistical methods assess relationships between variables. It covers the definitions of dependent and independent variables, the least squares method for estimating regression equations, and provides examples to illustrate these concepts. Additionally, it discusses the coefficient of determination and various assumptions underlying regression analysis.