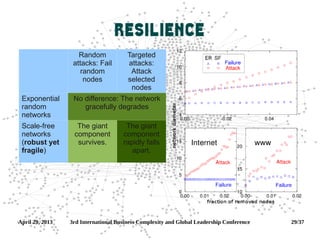
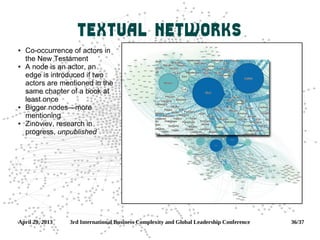
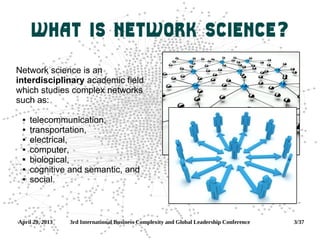
Network Science workshop

April 29, 2013 3rd International Business Complexity and Global Leadership Conference 1/37
WARNING!
Network Science is extremely
contagious ONCE YOU LEARN IT you. ,
START seeing Networks everywhere.
D Zinoviev.

Outline
●
What Is Network Science?
●
Terms and Definitions
●
Measures
●
Formation
●
Complex Behavior
●
Tools of the Craft
●
Unusual Applications of Network Science

What is Network Science?
Network science is an
interdisciplinary academic field
which studies complex networks
such as:
 telecommunication,
 transportation,
 electrical,
 computer,
 biological,
 cognitive and semantic, and
 social.

What is it based upon?
The field draws on theories and methods including:
 Graph theory from mathematics (Erdős, Rényi, Strogatz),
 Game theory from economics (Jackson),
 Statistical mechanics from physics (Barabási, Newman, Vespignani,
Watts),
 Data mining and information visualization from computer science
(Adamic), and
 Social structure from sociology (Watts).

Terms and definitions
● Network = Graph
● Nodes (vertexes, actors, members)
represent entities
● Nodes have properties (gender,
capacity, political view)
● Edges (arcs, links, ties) represent
relationships
● Edges have properties (direction,
weight, kind)
● Directed vs undirected
● Multigraph: graph with parallel
edges
● Simple graph: undirected, no loops,
no parallel edges
● Connected graphs
Boston SSAlbany
Brunswick
Boston NS
St Albans
Providence
Hartford
Springfield
New Haven
New York PS
Montreal
Rutland

Adjacency Matrix A
7
5
Boston SSAlbany
Brunswick
Boston NS
St Albans
Providence
Hartford
Springfield
New Haven
New York PS
Montreal
6 Rutland
9
12
11
4
8
1
3
2
10
A=

0 0 1 0 0 0 0 1 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0
1 1 0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 0 1 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0
0 0 1 1 1 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0 1 1 0 0
0 0 0 0 0 0 1 1 0 0 0 0
0 0 0 1 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 1 0

Aij
=1 if and only if i and j are connected

Incidence Matrix B
B=

1 0 1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0 0
0 1 1 0 0 0 0 0 0 0 0 0
0 0 1 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 1 0 1 0 0 0
0 0 0 0 0 0 0 1 0 1 0 0
0 0 0 1 0 0 0 0 0 1 0 0
0 0 0 1 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 1 0 1 0 0 0 0 0
 7
5
Boston SSAlbany
Brunswick
Boston NS
St Albans
Providence
Hartford
Springfield
New Haven
New York PS
Montreal
6 Rutland
9
12
11
4
8
1
3
2
10
A
B
C D
E
F
G
H
I
J
KL
Bij
=1 if and only if node i is incident to edge j
edges
nodes
A=B2
−2I

PATHS
7
5
Boston SSAlbany
Brunswick
Boston NS
St Albans
Providence
Hartford
Springfield
New Haven
New York PS
Montreal
6 Rutland
9
12
11
4
8
1
3
2
10
A
B
C D
E
F
G
H
I
J
KL
 Path = sequence of connected
edges (e.g., B – H – I)
 Can be simple (no self-
intersections)
 Can be a loop (ends where it
starts)
 Paths have lengths
 Geodesic = a shortest path (B
– F – G – J is not a geodesic,
but B – H – I is)
 What if edges are weighted?

Small World
 We are on average just 4–6 links
(“handshakes”) away from any other living
person on Earth (Milgram's experiment)—
thence, “six degrees of separation”
 Not all networks have the “small world”
property
I
Someone
I know
Boris
Berezovsky
Vladimir
Putin
Barak
Obama
W
ait, how
do you know
Obama?

Centrality
●
How “central” is a node
in the network?
●
Possibly affects
influence, resilience,
susceptibility, etc.
●
Several flavors: degree,
closeness,
betweenness,
eigenvalue, etc.

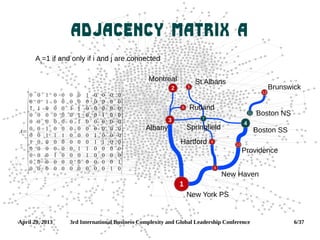
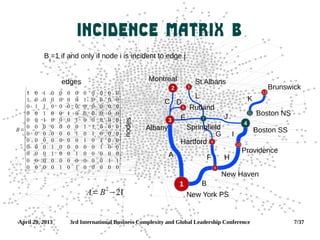
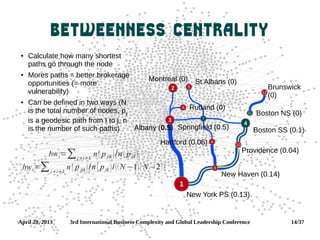
Degree Centrality[ ]
7
5
Boston SS (2)Albany (4)
Brunswick
(1)
Boston NS (1)
St Albans (1)
Providence (2)
Springfield (4)
New Haven (3)
New York PS (2)
Montreal (1)
6 Rutland (1)
9
12
11
4
8
1
3
2
10
Hartford (2)
 Just count the neighbors!
 More neighbors = more
“friends” = more importance
 Distinguish in-degree, out-
degree, and [total] degree
 Can be defined in two ways (N
is the total number of nodes,
aij
∈A):
di=∑j
aij
di=∑j
aij / N −1

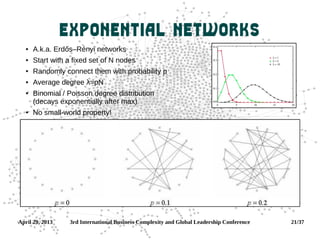
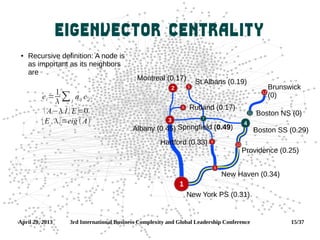
Degree Distribution
 Degree [centrality]
distribution is an
important network
measure—it relates
to the network
formation process
 Most common
distributions in
complex networks:
binomial (Poisson
for n→∞) and
power law (a.k.a.
Pareto, Zipf, scale
free)
 Why it is what it
is?

Closeness Centrality
7
5
Boston SS (0.5)
Brunswick
(1)
Boston NS (1)
St Albans (0.4)
Providence (0.4)
Springfield (0.6)
New Haven (0.5)
New York PS (0.5)
Montreal (0.4)
6 Rutland (0.4)
9
12
11
4
8
1
3
2
10
Hartford (0.5)
Albany (0.6)
 Calculate average inverse
shortest path to all other nodes
 Shorter path = closer “friends”
= better connectivity
is the total number of nodes, pij
is a geodesic path from I to j)
 Takes care of disconnected
networks!
ci=∑j
1/ pij
ci=∑j
1/ pij/ N −1

Betweenness Centrality
7
5
Boston SS (0.1)
Brunswick
(0)
Boston NS (0)
St Albans (0)
Providence (0.04)
Springfield (0.5)
New Haven (0.14)
New York PS (0.13)
Montreal (0)
6 Rutland (0)
9
12
11
4
8
1
3
2
10Hartford (0.06)
Albany (0.5)
 Calculate how many shortest
paths go through the node
 Mores paths = better brokerage
opportunities (= more
vulnerability)
is the total number of nodes, pij
is a geodesic path from I to j, n
is the number of such paths)
bwi=∑j≠i≠k
n pjik /n p jk 
bwi=∑j≠i≠k
n p jik /n pjk /N −1 N −2

Eigenvector Centrality
7
5
Boston SS (0.29)
Brunswick
(0)
Boston NS (0)
St Albans (0.19)
Providence (0.25)
Springfield (0.49)
New Haven (0.34)
New York PS (0.31)
Montreal (0.17)
6 Rutland (0.17)
9
12
11
4
8
1
3
2
10Hartford (0.33)
Albany (0.45)
 Recursive definition: A node is
as important as its neighbors
are
ei=
1
 ∑j
aij e j
 A− I  E=0
 E ,=eig A

Similarity and Triadic Closure
Connectivity between nodes may imply
similarity: A is connected to B  A is
similar to B (known as homophily in
social networks). Two dyads sharing a
node become a triad.
A
B
C
A
B
C
Alternative interpretation: weak ties
become strong ties (Granovetter).
A
B
C A
B
C

Clustering Coefficient
 Clustering coefficient of a
node with n neighbors:
 Ci
=0 — star
 Ci
=1 — clique (1, 4, 5, 6)
 C1
=6/10
 Average clustering
coefficient:
C=(.6+.67+1+1+1+1)/6=.88
Ci=2
∑j , k
aij aik a jk
nn−1
“Birds of a feather
flock together...”
(William Turner)
1 (.6)
2 (.67)
3 (1.)
4 (1.)
5 (1.)
6 (1.)

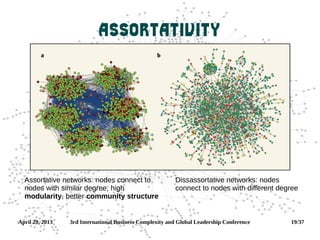
Modularity and Components
 NSSI (self-cutters) online
communities in LiveJournal (blogging
social Web site) form six
components
 If these two components are merged,
they form a giant component
 Modularity Q∈[-1, 1] measures the
density of links inside clusters as
compared to links between clusters:
Q=
∑ij
[aij −
∑i
aij ∑j
aij
∑ij
aij ]ij
∑ij
aij

Assortativity
Assortative networks: nodes connect to
nodes with similar degree; high
modularity, better community structure
Dissassortative networks: nodes
connect to nodes with different degree

Network Formation
●
Networks are complex
systems composed of
interconnected parts that
as a whole exhibit
properties not obvious
from the properties of the
individual parts.
●
Most networks are not an
immediate product of
intelligent design.

exponential Networks
 A.k.a. Erdős–Rényi networks
 Start with a fixed set of N nodes
 Randomly connect them with probability p
 Average degree λ=pN
 Binomial / Poisson degree distribution
(decays exponentially after max)
 No small-world property!

Small World Networks
 A.k.a. Watts–Strogatz networks
 Connect each node to its m neighbors
 Rewire the connections with probability β
 Degree distribution: δ-function for β→0, binomial/Poisson
for β→1 (unrealistic)
 Small-world—but no clustering!
β=0
0<β<1
β=1

Scale Free Networks
 A.k.a. Barabási–Albert networks
 Start with few nodes
 Attach a new node X to m existing nodes
Yi
with probability proportional to the
degrees of Yi
(preferential attachment)
 Power law degree distribution
 Small-world, community structure
 No meaningful average degree (scale-
free)
 Fat tail

Strategic Network formation
 Formed on purpose
 Add links to maximize utility: either
globally or pairwise
 Topology depends on the costs and
benefits
 Link cost c
 Benefit from direct
connection δ
 Benefits from indirect
connections δ2
, δ3
, δ4
,
etc.
3δ-3c
3δ-3c
3δ-3c
3δ-3c
δ+2δ2
-c3δ-3c
δ+2δ2
-cδ+2δ2
-c
0
0
0
0
δ vs c
“cheap” links
“expensive”links

Complex Behaviors
●
Simple contagion: epidemics, rumor
propagation
●
Complex contagion: collective action,
political views, fashion
●
Information diffusion: effect of
feedback
●
Resilience

Simple Contagion
 Susceptible – Infectious – Susceptible (SIS): At each step, a “healthy” (but
susceptible) node gets infected by an infected neighbor with probability p, and an
infected node recovers with probability r
 Susceptible – Infectious – Recovered (SIR): same as in SIS, but a node cannot
be reinfected
 Spreads fast in power-law networks

Collective Action
 A node becomes infected with probability p when either a certain
number M or a certain fraction m of its neighbors is infectious
✔ “I will wear red pants if at least 50% of my friends wear red
pants.”
✔ “I will use protocol X if at least 10 of my partners support
protocol X.”
✔ “I will go to protest tax hikes if all my friends go with me.”
✔ “I will feel happy if people around me are happy.”
 Supported by community structure:
✔ Structural trapping (few external links)
✔ Social reinforcement (many internal links)
✔ Homophily (“connected” means “similar”)
 Success depends on the point of origin

Information Diffusion
 A network of senders and receivers
 Each actor has knowledge, credibility,
and popularity
 Options for sender (speaker):
 To send (gain popularity, gain or lose
credibility)
 Not to send (lose popularity)
 Options for receiver (listener):
 Listen silently (gain knowledge, lose
popularity)
 Listen and provide feedback (gain
knowledge, gain popularity, gain or
lose credibility)
 Action based on Nash equilibrium

Resilience
Random
attacks: Fail
random
nodes
Targeted
attacks:
Attack
selected
nodes
Exponential
random
networks
No difference: The network
gracefully degrades
Scale-free
networks
(robust yet
fragile)
The giant
component
survives.
The giant
component
rapidly falls
apart.

Tools of the Craft
●
Gephi—graph visualization
●
Pajek—network algorithms and some
visualization
●
NetLogo—simple simulation environment (good
for small-scale experiments)
●
CFinder—community finder
●
NodeXL—network visualization plugin for Excel
●
networkx—Python library for network
algorithms

Gephi
 Network
Science
“Paintbrush”
 Analysis and
visualization
of large
networks
 Windows,
Linux, MacOS
 Developed by
Gephi
consortium
 Free and open
source

Pajek
 “Spider” in
Slovene
 Analysis and
visualization of
large networks
 Windows (run
on Linux in
wine)
 Developed by
Batagelj and
Mrvar
 Free, but not
open source

Unusual applications
Reminder:
If all you know is Network Science
everything looks like a Network.

Unusual networks
●
Networks of recipes and cooking ingredients
(Adamic)
●
Product space networks (Hidalgo)
●
Human disease networks (Barabási)
●
Flavor networks (Ahn)
●
Soccer player networks (Onody / de Castro)
●
And more!..

Semantic networks
 Two words are similar if they
are used by similar people
 (But two people are similar if
they use similar words!)
 Zinoviev, Stefanescu,
Swenson, and Fireman,
“Semantic Networks of
Interests in Online NSSI
Communities,” Proc. of
Workshop “Words and
Networks,” Evanston, IL,
June 2012

Textual Networks
 Co-occurrence of actors in
the New Testament
 A node is an actor, an
edge is introduced if two
actors are mentioned in the
same chapter of a book at
least once
 Bigger nodes—more
mentioning
 Zinoviev, research in
progress, unpublished

Thank you!

Network Science workshop

More Related Content

Similar to Network Science workshop

More from Dmitry Zinoviev

Recently uploaded

Network Science workshop