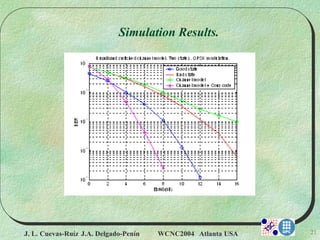
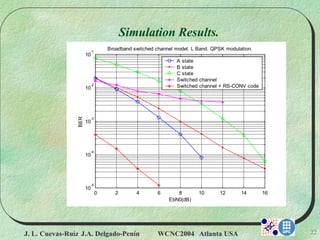
The document proposes a new statistical switched broadband channel model for high-altitude platform system (HAPS) links using three propagation modes. It describes the HAPS system and advantages, the switched channel model using a three-state Markov chain to represent changing propagation conditions, and simulation results showing error performance with two and three state models. The three state model more realistically represents HAPS channels and performs worse than a two state model due to increased variability in channel conditions.

1. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 1
“A Statistical switched broadband channel
model for a HAPS links”
José Luis Cuevas-Ruíz José A. Delgado-Penín
Presented by J.A. Delgado-Penín
Department of Signal Theory and Communications
Universitat Politècnica de Catalunya
Barcelona, Spain

2. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 2
Objective
To propose a new statistical switched
broadband channel model in L band for HAPS links
using three kinds of propagation modes (three
states).

3. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 3
Outline
• Overview.
• What the HAPS systems are?
• HAPS vs Terrestrial Systems
• Features
• Switched channel model.
• Three states Markov chain.
• Three states semi-Markov chain.
• Data from ITU-R (681-6).

4. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 4
Outline
• Broadband channels models.
• Bello´s model.
• Switched broadband channel.
• Two states.
• Three states
• Simulation results.
• Conclusions.

5. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 5
Overview.
What the HAPS systems are?

6. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 6
HAPS Advantages :
Serve a large number of people from a
distance –Less obstructions.
Provide Line of Sight Communications –
Higher Frequencies – Higher Data Rates
Portable – Can be re-positioned at any time.
Affordable – Cheaper than the terrestrial and
Satellite infrastructure.
HAPS Disadvantages :
Station Keeping – Need to make sure
that users can maintain tracking.
Clouds and Rain can significantly
attenuate the signal.
Overview.
HAPS vs Terrestrial Systems

7. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 7
Coverage areas
Semi-urban Urban Rural
HAP
h=21-25 km
Area
Angle of
Elevación
Coverage (radio. km)
h=21 km h=25 km
Urban 90-30 0-36 0-43
Semi-urban 30-15 36-76.5 43-90.5
Rural 15-5 76.5-203 90.5-
Features.
Coverage.

8. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 8
h
SPP
θ
receiver
d
shadowing
Multipath
Features.
Propagation effects.
LOS

9. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 9
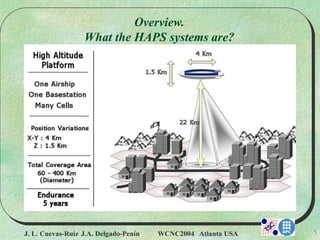
• Height of the ship ( 21-25 km).
• Angle of reception (θ) .
• Distance of SPP (d). }
•The shadowing level is a function of the angle of
reception and the distance of the receiver to the SPP.
• Inside the urban area a LOS condition can be supposed
(a Rice constant, K, with a high value).
• If the angle of reception diminishes then the multipath
effect increase (diminishes K value) [1].
COVERAGE
AREA{Geometrical
characteristics
Features.

10. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 10
Switched Channel Model.
Markov Chain
As the environmental properties change, the received
signal cannot be represented by a model with constant
parameters. This dynamic behavior was implemented in
the model using a Markov chain.
A state B state
C state
P BA
P CB
P BC
P AC
P CA
P AB
A state B state
C state
P BA
P CB
P BC
P AC
P CA
A state B state
C stateC state
P BA
P CB
P BC
P AC
P CA
P AB
P BCP BCP BC
PCC
PBB
PAA

11. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 11
The transitions between states are determined by a
matrix P, where each element Pij represent the
probability that the channel changes from the i to the j
state. For the channel model with three states A, B and
C, is defined the transitions matrix P
Switched Channel Model.
Markov Chain

12. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 12
A stationary state vector π is calculated, using the
properties of the Markov processes expressed by
where I is the identity matrix, P is the transition
matrix and e= [1 1 ….]T [7]. Each element πi represent
the percentage of the total time that the processes
remains in the i state.
π (I-P) = 0
π e = 1
π = ( πA πB πC )
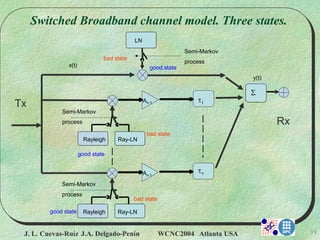
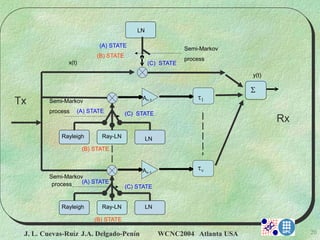
Switched Channel Model.
Markov Chain

13. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 13
A semi-Markov process is a Markov chain where the time
between changes of states are random and defined for
some kind of distribution. From the Markov process, a
new semi-Markovian process is defined. This process will
be described by a new transition matrix r, which is
calculated using
Switched Channel Model.
Semi-Markov Chain

14. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 14
Semi-Markovian Processes
Some distributions are described for fade
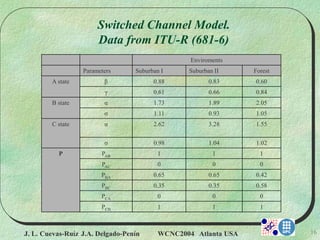
duration in the ITU-R Recommendation P.681-6
[8]. In this Recommendation are defined three types
of channel:
A state. LOS condition.
B state. Slight shadowing.
C state. Total obstruction.
A s t a t e B s t a t e
C s t a t e
P B A
P C B
P B C
P A C
P C A
P A B
A s t a t e B s t a t e
C s t a t e
P B A
P C B
P B C
P A C
P C A
A s t a t e B s t a t e
C s t a t eC s t a t e
P B A
P C B
P B C
P A C
P C A
P A B
Switched Channel Model.
Markov Chain

15. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 15
For the A state, the duration follows an exponential
distribution given by
)
where the parameters β and γ are in function of the level of
the shadowing and for d > β1/γ . The duration for the others
states follows a lognormal distribution valid for d > 0.1 m,
and is expressed as
where σ is the standard deviation of ln(d), the mean value of
ln(d) is ln(α) and the error function is defined in the ITU-R.
Switched Channel Model.
Markov Chain

16. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 16
Enviroments
Parameters Suburban I Suburban II Forest
A state β 0.88 0.83 0.60
γ 0.61 0.66 0.84
B state α 1.73 1.89 2.05
σ 1.11 0.93 1.05
C state α 2.62 3.28 1.55
σ 0.98 1.04 1.02
P PAB 1 1 1
PAC 0 0 0
PBA 0.65 0.65 0.42
PBC 0.35 0.35 0.58
PCA 0 0 0
PCB 1 1 1
Switched Channel Model.
Data from ITU-R (681-6)

17. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 17
Broadband channel model.
Bello`s Model
τi
τi τi
A
Σ
x(t )
y(t )
a(t) a(t ) a(t ) a(t )
τ1
τ2 τn
A0
Σ
x(t )
y(t )
a(t) a(t ) a(t ) a(t )
A1 A2 An

18. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 18
Switched Broadband channel model.
Two states
Semi -Markov
process
Rayleigh Ray-Ln
Rayleigh Ray-Ln
A1
An
y(t)
x(t)
bad state
good state
Lognormal
bad state
good state
τ1
τn
Σ
An-1
tn-1
Semi -Markov
process
Semi -Markov
process
Semi -Markov
process
Rayleigh Ray-LN-
Rayleigh Ray-LN
A1
An
y(t)
x(t)
bad state
good state
LN
bad state
good state
τ1
τn
Σ
An-1
tn-1
Semi -Markov
process
Semi -Markov
process

19. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 19
x(t)
bad state
good state
LN
Semi-Markov
process
Tx
Rx
y(t)
good state
Σ
An-1
Rayleigh Ray-LN
Semi-Markov
process
τ1
bad state
good state
An-1
Rayleigh Ray-LN
Semi-Markov
process
τν
bad state
Switched Broadband channel model. Three states.

20. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 20
x(t)
LN
Semi-Markov
process
Tx
Rx
y(t)
Σ
An-1
Rayleigh Ray-LN
Semi-Markov
process
τ1
An-1
Semi-Markov
process
τν
Rayleigh Ray-LN LN
(A) STATE
(A) STATE
(A) STATE
(B) STATE
(B) STATE
(B) STATE
(C) STATE
(C) STATE
(C) STATE
(C) STATE
LN

21. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 21
Simulation Results.

22. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 22
0 2 4 6 8 10 12 14 16
10
-5
10
-4
10
-3
10
-2
10
-1
Broadband switched channel model. L Band. QPSK modulation.
EbN0(dB)
BER
A state
B state
C state
Switched channel
Switched channel + RS-CONV code
Simulation Results.

23. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 23
Conclusions.
• A switched broadband channel model for L (2GHz)
band was proposed for HAPS systems following ITU-R with
two and three states.
•The analysis by simulation indicates that when the number
of channel states increases the performance of the system is
worse. This situation represents a more realistic scenario
versus Bello´s model.

24. J. L. Cuevas-Ruíz J.A. Delgado-Penín WCNC2004 Atlanta USA 24
Thanks for your attention.
Questions!!