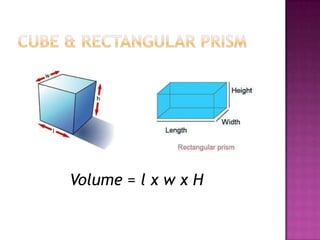
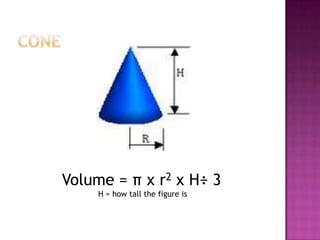
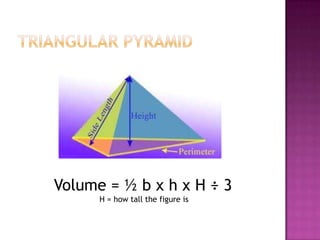
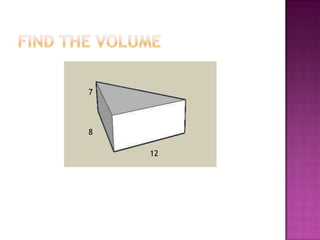
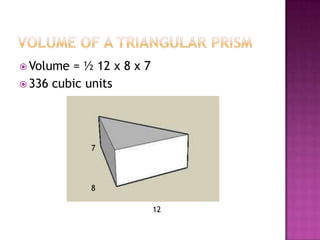
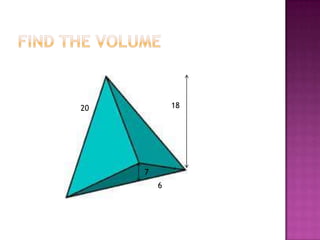
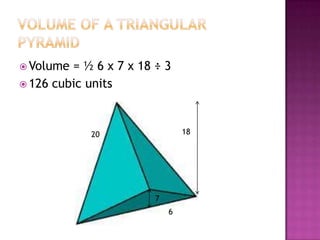
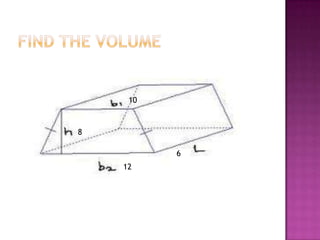
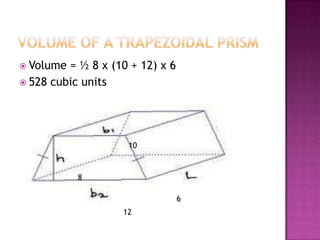
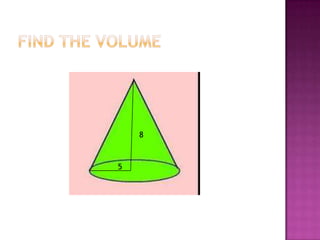
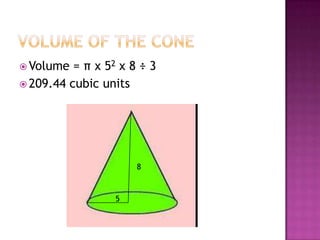
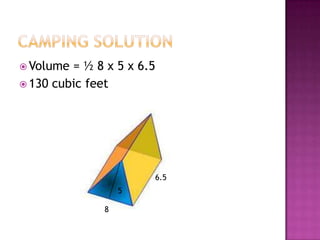
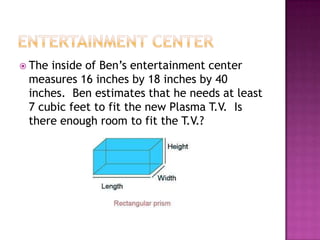
This document defines volume formulas for various shapes including cubes, rectangular prisms, triangular prisms, cylinders, rectangular pyramids, cones, spheres, and triangular pyramids. It provides examples of using the formulas to calculate volumes of specific objects. Practice problems at the end involve calculating volumes of objects like a tent, entertainment center, and ordered shapes by volume from least to greatest.

1. Volume8th Grade MathDefinitions and Examples

2. Cube & Rectangular PrismVolume = l x w x H

3. Triangular PrismVolume = ½ b x h x HH = how tall the figure is

4. CylinderVolume = πx r2x HH = how tall the figure is

5. Rectangular PyramidVolume = l x w x H ÷ 3H = how tall the figure is

6. ConeVolume = π x r2 x H÷ 3H = how tall the figure is

7. SphereVolume = 4/3 x π x r3

8. Triangular PyramidVolume = ½ b x h x H ÷ 3H = how tall the figure is

9. Find the Volume613

10. Volume of CylinderVolume = π x 62x 131470.27 cubic units613

11. Find the Volume7812

12. Volume of a Triangular PrismVolume = ½ 12 x 8 x 7336 cubic units7812

13. Find the volume182076

14. Volume of a triangular pyramidVolume = ½ 6 x 7 x 18 ÷ 3126 cubic units182076

15. Find the volume108612

16. Volume of a trapezoidal prismVolume = ½ 8 x (10 + 12) x 6528 cubic units108612

17. Find the Volume85

18. Volume of the coneVolume = π x 52x 8 ÷ 3209.44 cubic units85

19. Application of Volume ?’s

20. CampingA camping tent has a triangular end that measures 8 feet at the base and is 5 feet tall. The length of the tent is 6 ½ feet. What is the volume of the tent?

21. Camping SolutionVolume = ½ 8 x 5 x 6.5130 cubic feet6.558

22. Entertainment CenterThe inside of Ben’s entertainment center measures 16 inches by 18 inches by 40 inches. Ben estimates that he needs at least 7 cubic feet to fit the new Plasma T.V. Is there enough room to fit the T.V.?

23. Entertainment Center Solution40 x 16 x 18 11520 inches cubed, but we want cubic feet.12 inches in a foot cubed = 1728 feet.11520 ÷ 1728 = 6 2/3 feet cubed; not enough room401816

24. Least to Greatest VolumeA cone and a cylinder each have a diameter of 10 cm. A prism and a pyramid each have square bases that are 10 cm. on a side. All of the solids have a height of 8 cm. Order the solids according to their volume from least to greatest.

25. Least to Greatest Volume SolutionCone, Square Pyramid, Cylinder, Square Prismπ x 52 x 8 ÷ 3209.44810 x 10 x 8 ÷ 3266.678105105810 x 10 x 8800π x 52 x 8 628.3281010