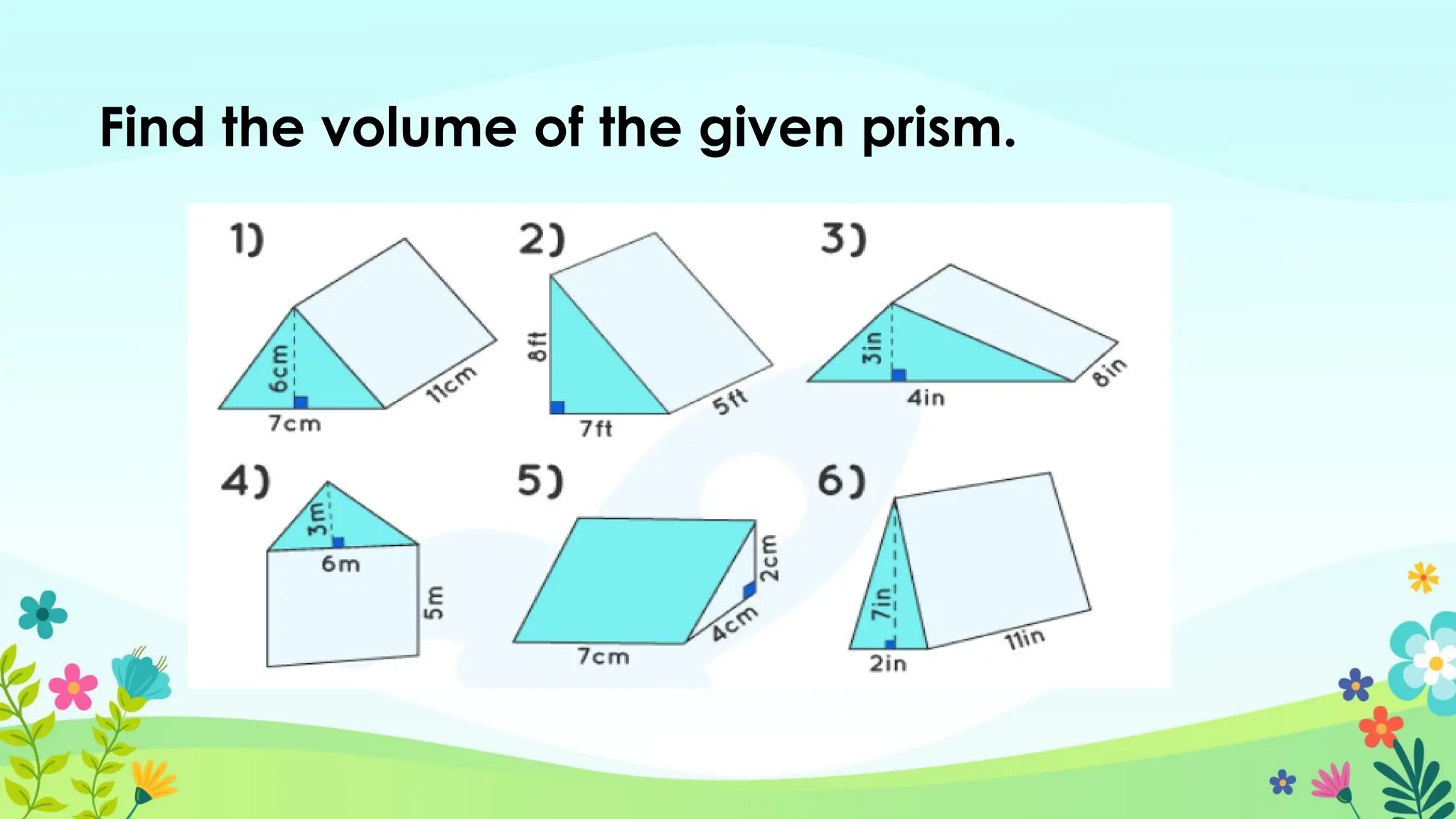
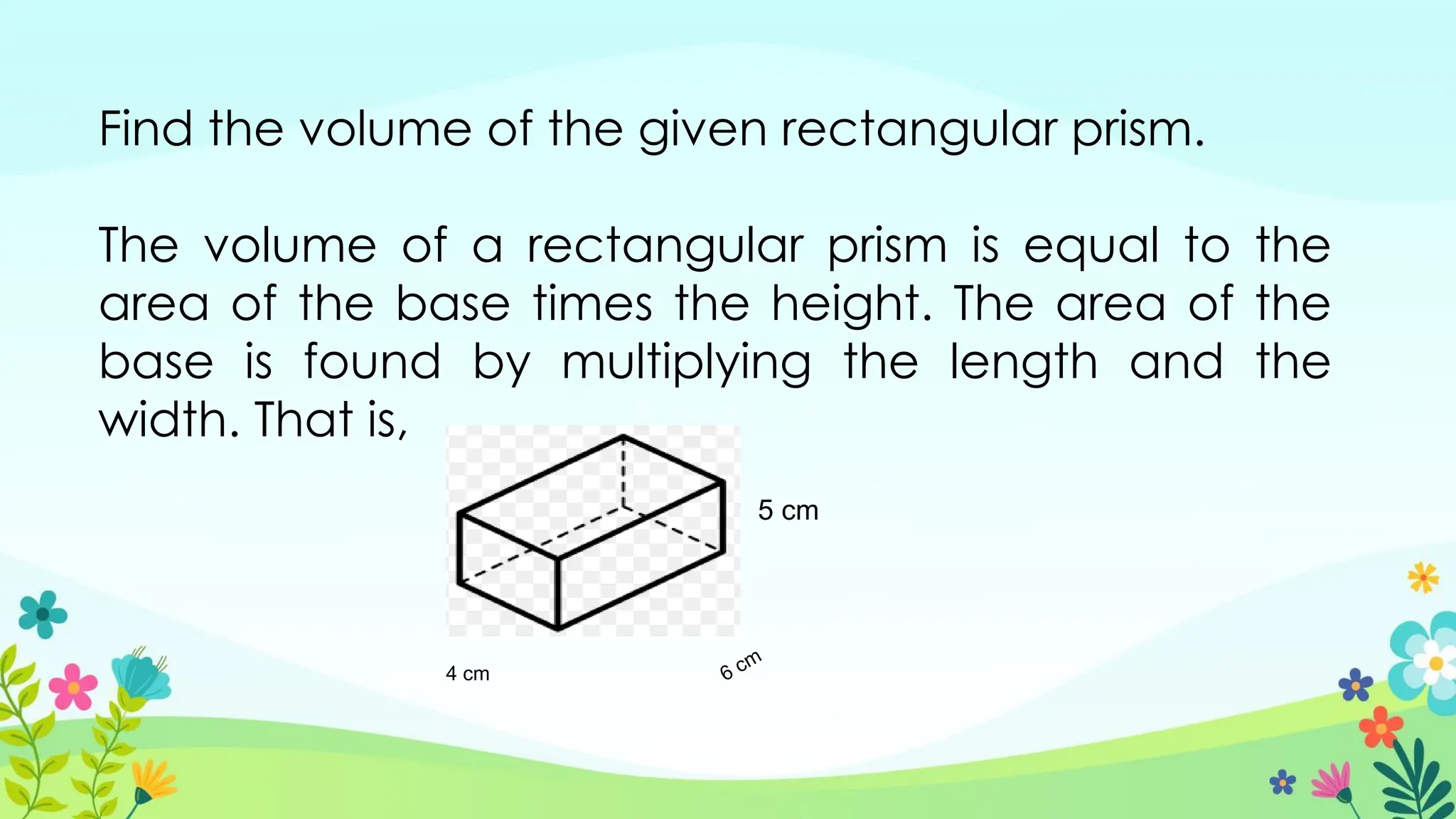
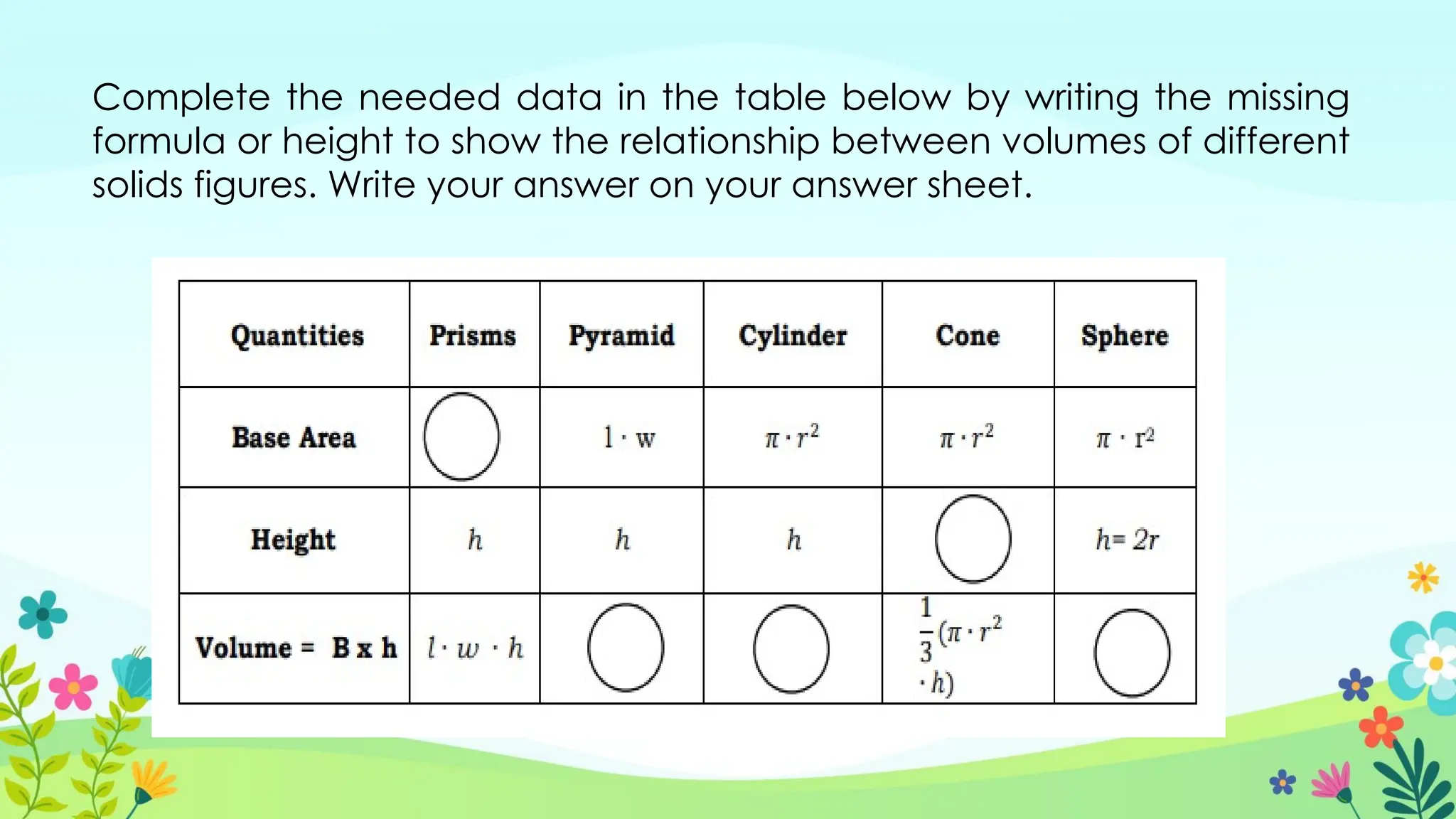
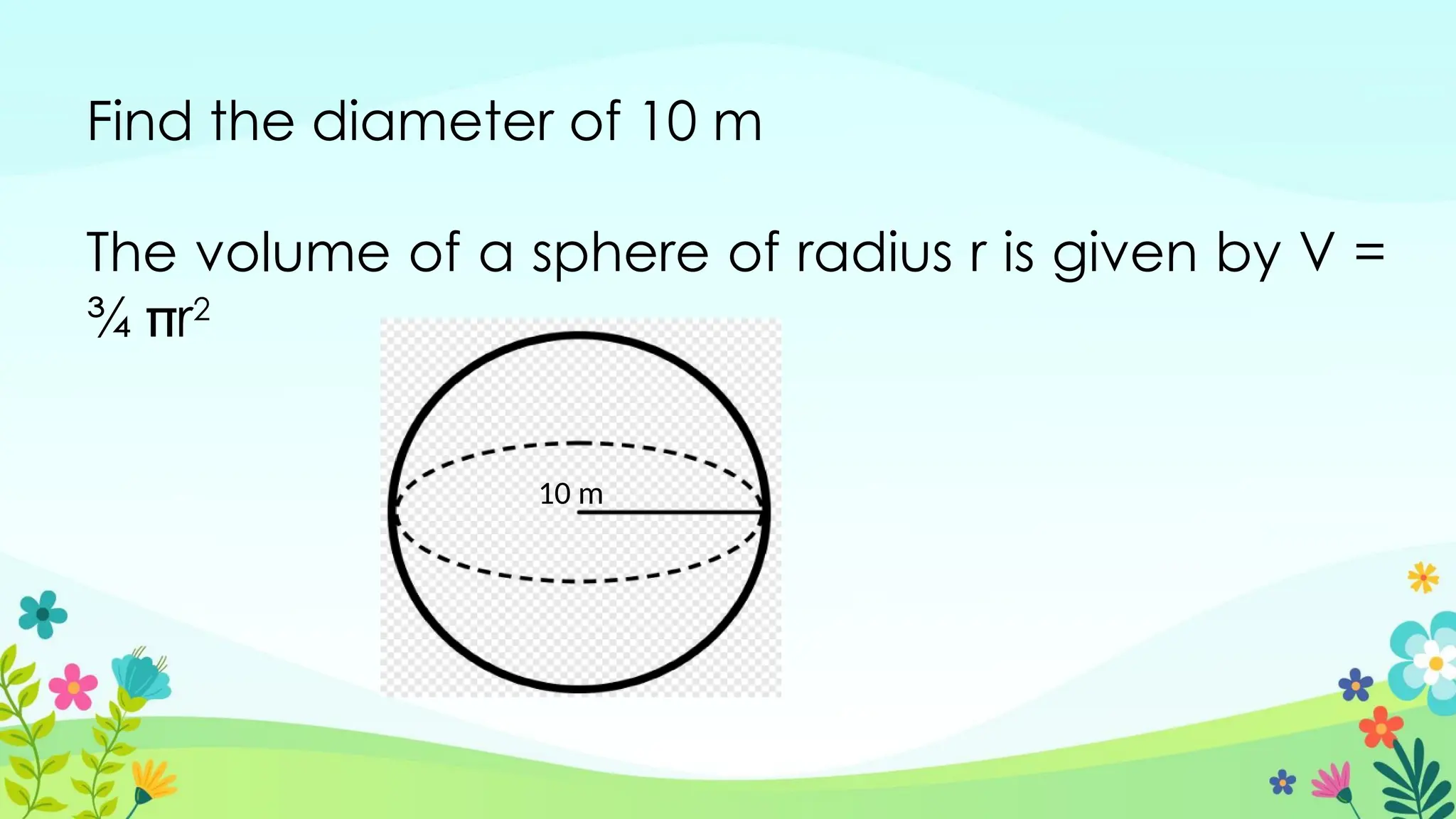
The document explores the concepts of volume in various geometric shapes, including prisms, pyramids, cylinders, cones, and spheres. It provides formulas for calculating the volume of these shapes and includes examples and exercises for practice. Additionally, it discusses the relationships between the volumes of different geometric figures.

1. MATH
Determining the Relationship of
Volume Between a Rectangular Prism
and a Pyramid; a Cylinder, and a Cone;
a Cylinder and Sphere
QUARTER 4 WEEK 1
D
A
Y
1

2. Let’s measure!
Needed Materials: can of milk, lunch box, can of
sardines, shoebox, pencil case, chocolate bar, water jag,
ice cream cone.
- Tape measure or any measuring material
Objects Length Width Height
1 can of milk
2. lunch box
3. can of sardines
4. shoebox
5. pencil case
6. chocolate bar
7. water jag
8. ice cream cone

3. 1. What are the
measurements?
2. What is volume?

4. The Tule Mat Lodge was typical structure used as
a shelter or house by many tribes of the Plateau
cultural group. These homes were usually
occupied from mid-October to mid-March. A
mat house was built roughly in the shape of
triangular prism.
13 ft
15 ft
1
1
f
t
.

5. What is the volume of the figure given above?
Source: ‘Native American House”
Volume is the amount of space in a solid figure. It
is measured in cubic units, such as cubic
centimeter (cm3
), cubic meter (m3
), and cubic
millimeter (mm3
).

6. Example 1: Find the volume of a Tule Mat Lodge describe
above.
The volume of a prism is computed by the formula:
Volume = area of base x height, or V=Bh
The volume of a triangular prism is equal to the area of the
base ( A = (1/2) bh) times the height of the triangular prism.
(V= (1/2)ba)xh
Where b = base of triangle
a = altitude of triangle
h = height of triangular prism 13 ft
15 ft
1
1
f
t
.

7. Solution:
V = (1/2 ba)h
= (1/2 x 13 x 11) x 15
= 71.5 x 15
= 1 072.5 cu.ft

8. Find the volume of each triangular prism.
1.
height of the base: 12 cm
length of base: 14 cm
height of prism: 16 cm
______________________
2.
height of the base: 8.5 ft
length of the base: 12.5 ft
height of prism: 13.5 ft

9. Answer the following:
1. The base area of a triangular
prism is 55 square ft. Find thevolume
if the length is 20 ft.
2. The triangular prism has a height
of 16 yards and a base with area of
169 square yards. What is a
volume?

10. Find the volume of the given prism.

11. MATH
Determining the Relationship of
Volume Between a Rectangular
Prism and a Pyramid; a Cylinder,
and a Cone; a Cylinder and Sphere
QUARTER 4 WEEK 1
D
A
Y
2

12. Let’s try it!
Solve the following problem:
1. The side of the base of a square pyramid is 5 yrd..
What is the volume of the square pyramid if its
height is 6 yrds?

13. Find the volume of the given rectangular prism.
The volume of a rectangular prism is equal to the
area of the base times the height. The area of the
base is found by multiplying the length and the
width. That is,
4 cm 6 cm
5 cm

14. Solution:
V = area of the base x height
V = Bh
= (l x w) x h
= l x w x h
= 6 x 5 x 4
V= 120 cubic centimeter or 120 cu. Cm
Therefore: the volume of the rectangular prism is 120
cubic cm.

15. Find the volume of each rectangular prism.
1. length: 8.2 cm
width: 5.5 cm
height: 10 cm
2. length: 25.4 m
width: 12 m
height: 11 m
3. length: 35 ft.
width: 25 ft.
height: 12 ft.

16. Complete the needed data in the table below by writing the missing
formula or height to show the relationship between volumes of different
solids figures. Write your answer on your answer sheet.

17. Read and answer each item below.
it on your answer sheet.
1. Claire makes models to show the relationship
between the volume of a rectangular prism and the
volume of a rectangular pyramid. The rectangular
prism model has a base area of 8 square inches and a
height of 12 inches. She also makes a rectangular
pyramid with a base and height congruent to the
corresponding parts of the prism. Which conclusion is
INCORRECT about the relationship between the
volumes of the models?

18. Solve the following:
1. A circular table has a radius of 2 m. What is its
circumference?
2. A triangular lot has edges measuring 16 m, and12 m. How
long should the fence be for the lot 2. A square has an
area of 49 sq. m What is its perimeter?

19. MATH
Determining the Relationship of
Volume Between a Rectangular
Prism and a Pyramid; a Cylinder,
and a Cone; a Cylinder and Sphere
QUARTER 4 WEEK 1
D
A
Y
3

20. What is the volume of a can of
milk with radius of 10 m and
height of 21 m?
How about the can of milk?
What kind of solid is it?
The volume of a cylinder is equal
to the area of circular base (r2
)
times the height of the cylinder.
10
21

21. V = r2
h
Given: r = 10 m; h= 21 m
Solution:
V = r2
h
= 3.14 x 102
x 21
= 3.14 x 100 x 21
V = 6 594 cu. m
Thus; the volume of the can of milk is 6 594 cu. m

22. Find the diameter of 10 m
The volume of a sphere of radius r is given by V =
¾ r2
10 m

23. Given = d = 10 m, where r = d/2 r = 10/2
r = 5 m
Solution:
V = 4/3 r3, with d = 10m, then r = 5
= 4/3 (3.14) (5)3
V = 523.33 cu. m

24. Read and answer each item below.
it on your answer sheet.
1. Claire makes models to show the relationship
between the volume of a rectangular prism and the
volume of a rectangular pyramid. The rectangular
prism model has a base area of 8 square inches and a
height of 12 inches. She also makes a rectangular
pyramid with a base and height congruent to the
corresponding parts of the prism. Which conclusion is
INCORRECT about the relationship between the
volumes of the models?

25. Relationship between the volume of the Cylinder and Cone.
1. Exploring the Volume of a Sphere Fill a cylinder with water. Push
a sphere with the same radius into the cylinder. Notice that about
2/3 of the water will be displaced. So the volume of the sphere is
2/3 of the volume of the cylinder.
The volume of the cylinder would be the area of its base times its
height, which is (𝜋𝑟2
)(2𝑟)𝑜𝑟 2𝜋𝑟3
. The sphere does not fill the
whole cylinder. In fact, the volume of the sphere is 2 3 of the
volume of the cylinder: 2/3 (2𝜋𝑟 3). Therefore, the volume of the
sphere is V = 4 /3 𝜋

26. Answer the following questions in your own words. Write your
answer in
your answer sheet.
1. What is the relationship between the volume of a prism and
a pyramid?
_____________________________________________________________
_____________________________________________________________
2. What can you say about the volume of prism and cylinder?
How are they
related?
_____________________________________________________________
_____________________________________________________________

27. Dino has a cone-shaped container that he
fills with water. He pours the water into the
cylindrical shaped container. Both
containers have the same height and
bases. Which of the following statements is
CORRECT after he pours the water from the
cone to the cylinder?

28. MATH
Determining the Relationship of
Volume Between a Rectangular Prism
and a Pyramid; a Cylinder, and a Cone;
a Cylinder and Sphere
QUARTER 4 WEEK 1
D
A
Y
4

29. Let’s answer the following question.
Instruction: Write in the blank TRUE if the given statement is
correct, otherwise write FALSE.
1. A box is an example of prism.
2. The base of a prism may be a triangle.
3. The curve surface of a cone is a rectangle.
4. The base of the cylinder is a square.
5. The volume of a sphere can be determined if its radius is
known.

30. Find the volume of each cylinder.
1. R = 5.4 cm : Height = 8 cm
2. R = 10.2 cm : Height = 28 cm
3. R = 7 dm : Height = 9 dm

31. To find the volume of the given pyramid whose length measures 9
cm, width of 4 cm and height of 6 cm.
Answer the following questions in your own words. Write your
answer in
your answer sheet.
1. Define volume.
_____________________________________________________________
2. How is the volume of cylinder related to the volume of the cone?
_____________________________________________________________3.
Compare the volume of a cylinder and a sphere. How are they
related?
_____________________________________________________________

32. MATH
Catch Up Friday
QUARTER 3 WEEK 8
D
A
Y
5