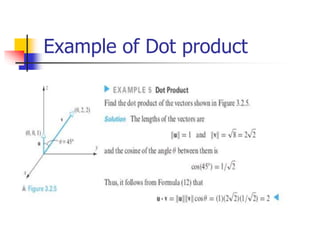
This document discusses vectors and their relationships in 2D and 3D space. It covers the dot product and how it can be used to determine the angle between two vectors. It also discusses properties of the dot product, orthogonal vectors, and using the dot product to find vector components. The document then covers planes in 3D space, including finding the point-normal equation of a plane and using vectors to write the equation of a plane. It provides examples of finding dot products, writing vector and parametric equations of planes and lines, and calculating distances between points and planes/lines.

1. 3.3 VECTORS
Dot Product;

2. The Angle Between Vectors
 Let u and v be two nonzero vectors in 2-space or
3-space, and assume these vectors have been
positioned so their initial points coincided. By the
angle between u and v, we shall mean the
angleθ determined by u and v that satisfies 0 ≤
θ ≤ π.

3. Dot Product
 If u and v are non zero vectors in R2 or R3 , and if θ is
the angle between u and v, then the dot product (also
called the Euclidean inner product) of u and v is denoted
by u · v and is defined as
 u · v = ∥u∥∥v∥ cos θ If u = 0 or v = 0, then we define u ·
v to be 0.
 Θ is acute if u·v >0. • θ is obtuse if u·v<0. • θ=π/2 if
u·v=0.

4. Example of Dot product

5. Component Form of the Dot
Product (1/2)

6. Component Form of the Dot
Product (2/2)
 The formula is also valid if u=0 or v=0.

7.  If u and v are nonzero vectors then
it also can be written as
Finding the Angle Between
Vectors

8. Dot Product

9. Example 3
Finding Dot products from Components

10. Theorem 3.3.2
Properties of the Dot Product
If u, v and w are vectors in 2- or 3-space
and k is a scalar, then:

11. Orthogonal Vectors

12. Example 4
A Vector Perpendicular to a Line
 Show that in 2-space the nonzero vector n=(a,b) is
perpendicular to the line ax+by+cz=0.
 Solution

13. Example 5
Vector Component of u Along a

14. Distance between Point &
Plane or line

15. Example 7
Using the Distance Formula

16. Planes in 3-Space
),,( 0000 zyxP 
0)()()(
0
is,thatn,toorthogonalisvectorthe
000
0
0


zzcyybxxa
PPn
PP

17. Example 1
Finding the Point-Normal
Equation of a Plane

18. Distance between Point &
Plane

19. Distance between Parallel
planes

20. 3.5 Lines and Planes
in 3-Space

21. 0)(
so,r-rThenplane.thetonormalvectora
bec)b,(a,nletand)z,y,(xPpointtheto
originthefromvectorthebe),,(let
0
00
0000
0000




rrn
PP
zyxr
Vector Form of Equation of a
Plane

22. Parametric equations of a
plane

23. Example 1
Vector Equation of a Plane

24. Example 2
Parametric Equations of a Line