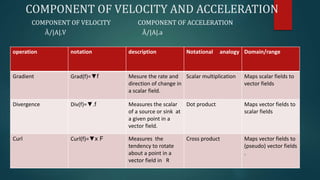
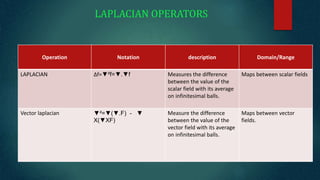
This document provides an introduction to vector calculus concepts. It defines key terms like velocity, acceleration, and gradient. It presents the formulas for calculating the gradient of a scalar function, unit normal vector, and components of velocity and acceleration. Additionally, it outlines vector operations like divergence, curl, and Laplacian operators; and provides examples of how to calculate a scalar potential, directional derivative, and conditions for solenoidal and irrotational vectors.

1. BY,
J. MANJULA
ASSISTANT PROFESSOR OF MATHEMATICS
BON SECOURS COLLEGE FOR WOMEN

2. INTRODUCTION
 Vector calculus was developed by J.WILLARD GIBBS and OLIVER
HEAVISIDENEAR.
 The end of the 19th century ,and most of the nation and terminology was
established by Gibbs and Edwin Bidwell Wilson in their 1901 book, vector
analysis.
 In the conventional form using cross product, vector calculus does not
generalize to higher dimensions.
 While the alternative approach of geometric algebra, which uses exterior
products does generalize as discussed below.

3. VELOCITY AND ACCELERATION
VELOCITY
 V=dr/dt where v the velocity . It is a
vector function of a scalar variable ‘t’.
Example:
r=4costi +4sintj+6tk
v=dr/dt
v=-4sinti+4costj+6k
ACCELERATION
 Acceleration is the rate of change of velocity
a=dv/dt
=d/dt(dr/dt)
Example:
v=-4sinti+4costj+6tk
a=dv/dt
A=-4costi-4sintj+ok

4. GRADIENT
Gradients of a scalar function. Let ф(x,y,z) be a scalar point function. Defiend in a certain
region of space .then the vector point function given by,
gradф= 𝑖 Әф/Әx+jӘф/Әy+kӘф/Әz
is defined as gradient of ф (or) gradф
UNIT NORMAL VECTOR
The vector normal to the surface of ф is
N^= GRAD Փ/|GRADФ|

5. COMPONENT OF VELOCITY AND ACCELERATION
COMPONENT OF VELOCITY
Ā/|A|.V
z
COMPONENT OF ACCELERATION
Ā/|A|.a
operation notation description Notational analogy Domain/range
Gradient Grad(f)=▼f Mesure the rate and
direction of change in
a scalar field.
Scalar multiplication Maps scalar fields to
vector fields
Divergence Div(f)=▼.f Measures the scalar
of a source or sink at
a given point in a
vector field.
Dot product Maps vector fields to
scalar fields
Curl Curl(f)=▼x F Measures the
tendency to rotate
about a point in a
vector field in R
Cross product Maps vector fields to
(pseudo) vector fields
.

6. FORMULA
Scalar potential ( find ф value) GIVEN ▼Փ
Directional derivative Grad ф.a^
Maximum value of directional derivative |grad ф|
Solenoidal vector (div f)=0 (or) ▼.F=0
Irrotational vector Curl F=0 (or) ▼x F=0

7. LAPLACIAN OPERATORS
Operation Notation description Domain/Range
LAPLACIAN ∆f=▼²f=▼.▼f Measures the difference
between the value of the
scalar field with its average
on infinitesimal balls.
Maps between scalar fields
Vector laplacian ▼²=▼(▼.F) - ▼
X(▼XF)
Measure the difference
between the value of the
vector field with its average
on infinitesimal balls.
Maps between vector
fields.

8. THANK YOU