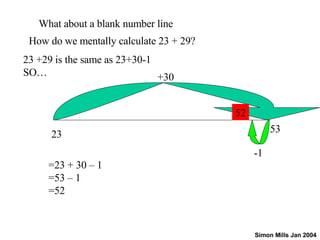
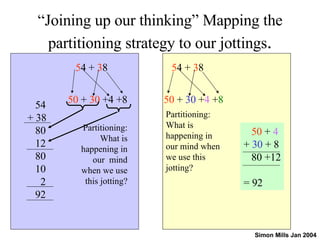
The document discusses teaching methods for addition and subtraction in primary numeracy by Simon Mills, highlighting the strategies of doubling multiples and finding pairs that total specific numbers. It emphasizes collaborative learning through discussions, informal jotting, and using different methods like partitioning and decomposition to simplify calculations. The teaching approach includes practicing mental calculations, exploring written methods, and challenges with larger numbers to enhance students' mathematical understanding.

1. Using Speaking and Listening to “Think Together” about standard written methods for Addition and Subtraction, in the Primary Numeracy Hour . By Mr Mills and Year 4 2004 Simon Mills Jan 2004

2. We observed the patterns that are made when you double multiples of 10, 100 and 1000. We found out that to double a multiple of ten you can can divide by 10, double the digit, and then multiply by 10 again So double 60 is the same as (60 ÷ 10) x 2 x 10 = (6 x 2) x 10 = 12 x 10 = 120 Did this work for doubling Multiples of 100 or 1000? Simon Mills Jan 2004

3. To double multiples of 100 or 1000 we found out that you can divide by the multiple, double the digit you are left with, then multiply by the same multiple again. So to double 200 Divide by 100 200 becomes 2 Double 2 Becomes 4 Multiply by 100 Become 400 Does this work for all Multiples of 100? To double 2000 Divide by 1000 2000 becomes 2 Double 2 Becomes 4 Multiply by 1000 Become 4000 Does this work for all Multiples of 1000? AND Simon Mills Jan 2004

4. What strategy could we use to total these numbers efficiently? 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 10 + 20 + 30 + 40 + 50 + 60 + 70 + 80 + 90 100 + 200 + 300 + 400 + 500 + 600 + 700 + 800 + 900 That was our challenge and to show how we did it. Simon Mills Jan 2004

5. Informal jottings + discussions = Thinking Together We are beginning to reason about numbers! Simon Mills Jan 2004

6. Firstly you find pairs of numbers which total 10 Then you count up the multiples of 10 There are 4 pairs of numbers which Total ten in the number sequence 1+9, 2+8, 3+7, 4+6 and the 5 is left Over 4 lots of 10 gives 40 Add the 5 And the total is 45 Can we use this strategy To help us find the other totals? For multiples of 10.. Find pairs which total 100? For multiples of 100 Find pairs which total 1000? Simon Mills Jan 2004

7. Adding multiples of 10 10+90, 20+80, 30+70, 40+60, total 100 each with 50 left over. 4 lots of 100 is 400 Add the 50 Total 450 Adding multiples of 100 100+900, 200+800, 300+700, 400+600, total 1000 each with 500 left over. 4 lots of 1000 is 4000 Add the 500 Total 4500 What else is special about the totals we have made? We thought about place value and what happens when we multiply numbers by 10, 100 or 1000! Our total pattern… 45, 450, 4500 Simon Mills Jan 2004

8. Can you use these strategies to carry out these calculations? 3 + 5 +7 + 6 + 4 80+ 70 + 20 + 60 + 30 Can we use what we know about place value to find a Shorter way to calculate the solutions to these number sentences based On the ones above? 30 + 50 +70 + 60 + 40 800+ 700 + 200 + 600 + 300 Simon Mills Jan 2004

9. We used the round to the nearest 10 and adjust strategy, for addition of 2 and 3 digit numbers How can we mentally calculate 23 + 29? Can we do this our heads? Maybe, but will we remember every step? Will a Jotting help, maybe but which one? Simon Mills Jan 2004

10. What about a blank number line How do we mentally calculate 23 + 29? 23 +30 -1 53 52 =23 + 30 – 1 =53 – 1 =52 23 +29 is the same as 23+30-1 SO… Simon Mills Jan 2004

11. Informal jottings + discussions = Thinking Together Working a problem Simon Mills Jan 2004

12. How could we carry out this calculation? = 54 + 38 What do we know? We know that “=“ means “the same as” So Is the same as or equal to 54 + 38 So The calculation can also be written as 54 + 38 = as well. What strategy might we use? In Talking twos we discussed and jotted our methods.!!! Simon Mills Jan 2004

13. Sharing methods we know + discussions = Thinking Together Working a problem Simon Mills Jan 2004

14. 54 +40 -2 94 92 54 +10 +6 +20 92 64 84 5 4 + 3 8 50 + 30 +4 +8 80 + 12 Which of these is the most efficient method or strategy? Blank Number Lines Partitioning Decompose and count on Round up and adjust Our Methods… 90 +2 92 Simon Mills Jan 2004

15. Is there a way we can use the strategies we know to develop a shorter jotting? 50 + 4 + 30 + 8 80 + 12 = 92 54 + 38 = 54 + 38 12 80 2 10 80 92 Addition can be done in any order How about this way? Or this? Which of the strategies we used before Are we using in these jottings? Can we map it to our calculation? Simon Mills Jan 2004 54 + 38 80 12 80 10 2 92

16. “ Joining up our thinking” Mapping the partitioning strategy to our jottings . 54 + 38 80 12 80 10 2 92 5 4 + 3 8 50 + 30 +4 +8 Partitioning: What is happening in our mind when we use this jotting? 5 4 + 3 8 50 + 30 + 4 + 8 Partitioning: What is happening in our mind when we use this jotting? Simon Mills Jan 2004 50 + 4 + 30 + 8 80 +12 = 92

17. Joining up our thinking Practice + jottings Talking + our actions + Partner + suggestion Thinking together Simon Mills Jan 2004 It’s good to talk, it helps us to share ideas, and join up our thinking with other people’s.

18. Group joined up thinking + Teacher Assessment = Small Group review + Whole Class Sweep + Teacher Review Simon Mills Jan 2004

19. Joining up our thinking. Using the mental methods we know to create a written method. Simon Mills Jan 2004

20. How would you calculate the answer to 94 +73 In talking twos we discussed strategies and then as individuals made jottings to show how we would carry out the calculation on whiteboards. We checked each others solutions, and talked about what we had done. Simon Mills Jan 2004

21. We had used a whole range of methods, to come up with the same solution, this was great because the methods we chose were all methods and mind maps of our thinking from last week Simon Mills Jan 2004

22. We shared our methods, and tried to explain them to the class. We tried to find out if they had anything in common. We used Power Point to review our work from last week, to see if this would help. Simon Mills Jan 2004

23. In all of our jottings we had used partitioning, or decomposition to help us break the calculation down into manageable chunks. 90 + 4 + 70 + 3 3 + 4 = 7 90 + 70=160 160 + 7 = 167 9 4 + 7 3 90 + 70 + 4 + 3 Partitioning: What is happening our mind when we use this jotting? 94 +3 +70 167 164 Decompose and count on 94 + 73 is the same as 94 + 70 +3 is the same as 164 + 3 is the same as 167 Simon Mills Jan 2004

24. In all of our jottings we had used partitioning, or decomposition to help us break the calculation down into manageable chunks. 9 4 + 7 3 90 + 70 4 + 3 167 9 4 + 7 3 90 + 70 + 4 + 3 Partitioning: What is happening our mind when we use this jotting? 3 + 4 = 90 + 70 = 160 + 7 = In our heads! On our think space 160 7 Simon Mills Jan 2004

25. Mr Mills listened and watched as we worked. He asked questions to help us explain what was going on in our minds. He joined in, and helped us to understand what was going on in our Class “think Space.” He said he wanted to use our ideas to help us to make the written calculation shorter. He did this by showing us a method and explaining how our ideas helped to make the method work. Simon Mills Jan 2004

26. 1) This is our calculation 2) Partition or decompose the numbers in the calculation 132 is the same as 100 + 30 + 2 56 is the same as 50 + 6 3) Write out you expanded numbers. Make sure that you write them so 100’s, 10s and 1s are in the same columns. 4) Total the columns, 1s first, then the 10s, then the 100s. And so on, record you totals under the column you have totalled ie 2 + 6 = 8 5) Recombine your total eg 100 + 80 + 8 = 188 Can you find your method or our mental Strategies in this written method? Simon Mills Jan 2004

27. We tried out the calculation method for ourselves using examples given to us to practice with. Some of us were so good Mr Mills challenged us to see what would happen If we had to use bigger Numbers. Would our method still work? How would the calculation change? We worked through the calculations together in our class think space at the end, and marked and checked each other’s work. We discussed how the method had worked and what happened with big numbers. Simon Mills Jan 2004

28. We explored how our written method for addition, might be used to carry out subtraction calculations Mr Mills talked us through and we had a go using examples given to us to practice with . We all found this a bit of a challenge. The big question was what to do with those addition signs? The last one was easy, but sometimes we forgot we had used them to help us partition or decompose our large number and instead of adding columns, this time we were subtracting them. The method got easier though as we got used to ignoring the addition signs until the end of our calculation. Can you find your method or our mental Strategies in this written method? Simon Mills Jan 2004