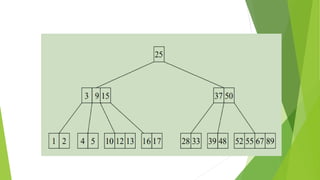
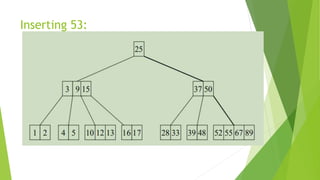
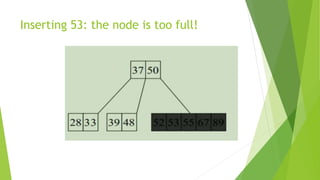
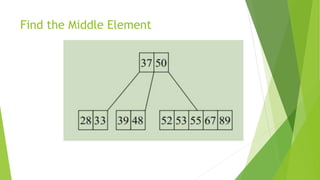
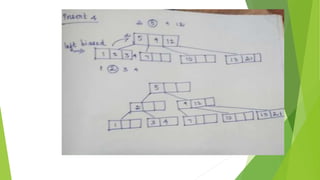
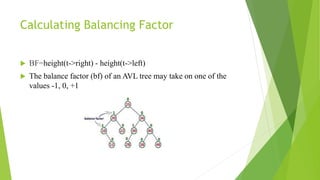
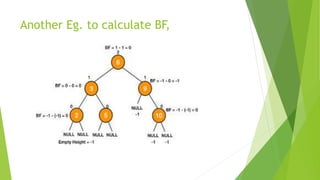
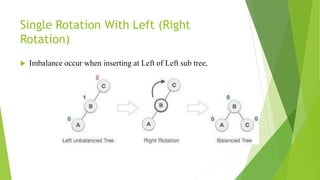
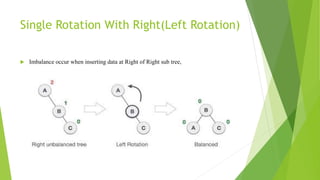
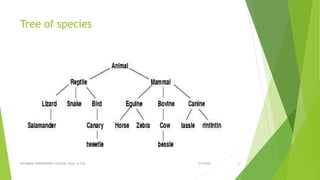
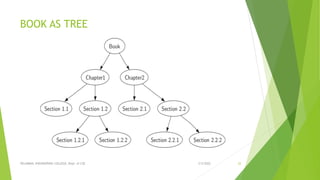
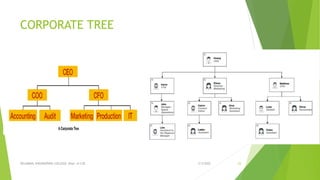
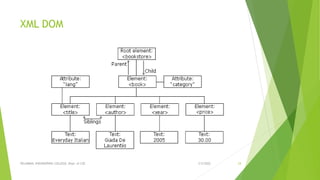
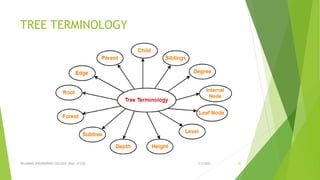
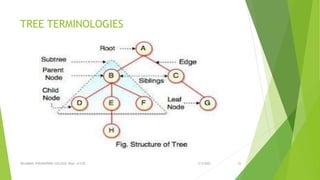
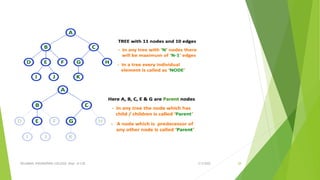
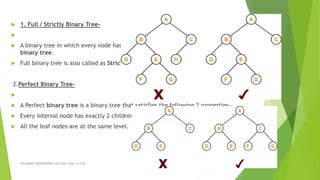
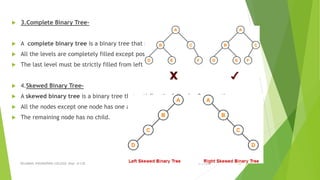
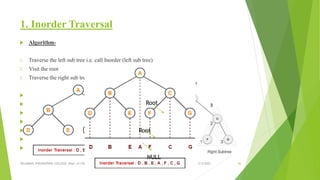
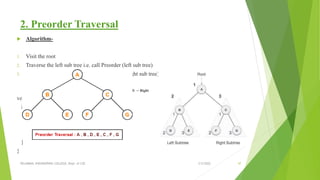
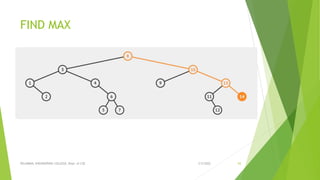
This document discusses binary search trees and AVL trees. It begins with an introduction to binary search trees and their properties. It then describes AVL trees, which are self-balancing binary search trees that ensure the height difference between any two subtrees of a node is at most 1. The document provides pseudocode for performing basic operations on AVL trees like insertion, single rotations, double rotations, and calculating the balancing factor. It also includes examples of calculating heights and balancing factors for AVL tree nodes.





























![3/5/2022
VELAMMAL ENGINEERING COLLEGE, Dept. of CSE 56
Algorithm:
Search (ROOT, ITEM)
•Step 1: IF ROOT -> DATA = ITEM OR
ROOT = NULL
Return ROOT
ELSE
IF ITEM < ROOT -> DATA
Return search(ROOT -> LEFT, ITEM)
ELSE
Return search(ROOT -> RIGHT,ITEM)
[END OF IF]
[END OF IF]
•Step 2: END](https://image.slidesharecdn.com/unitiii-220305070553/85/Unit-III-NON-LINEAR-DATA-STRUCTURES-56-320.jpg)


![3/5/2022
VELAMMAL ENGINEERING COLLEGE, Dept. of CSE 59
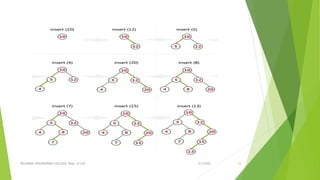
Insert (ROOT, ITEM)
•Step 1: IF ROOT = NULL
Allocate memory for TREE
SET ROOT -> DATA = ITEM
SET ROOT -> LEFT = ROOT -> RIGHT = NULL
ELSE
IF ITEM < ROOT -> DATA
Insert(ROOT -> LEFT, ITEM)
ELSE
Insert(ROOT -> RIGHT, ITEM)
[END OF IF]
[END OF IF]
•Step 2: END](https://image.slidesharecdn.com/unitiii-220305070553/85/Unit-III-NON-LINEAR-DATA-STRUCTURES-59-320.jpg)









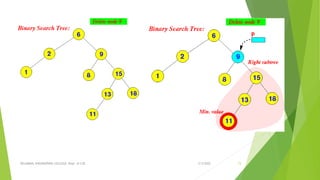
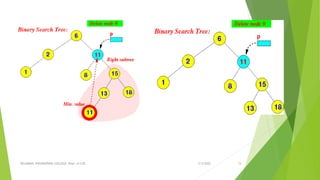
![ Algorithm
Delete (ROOT, ITEM)
Step 1: IF ROOT = NULL
Write "item not found in the tree"
// If the key to be deleted is smaller than the root's key,
then it lies in left subtree
ELSE IF ITEM < TREE -> DATA
Delete(ROOT->LEFT, ITEM)
// If the key to be deleted is greater than the root's key,
// then it lies in right subtree
ELSE IF ITEM > ROOT -> DATA
Delete(ROOT-> RIGHT, ITEM)
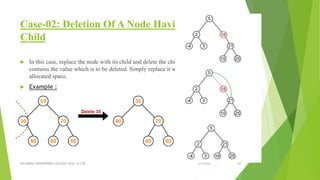
// node with two children: Get the inorder
predecessor(largest in the left subtree)
ELSE IF ROOT -> LEFT AND ROOT -> RIGHT
SET TEMP = findmax(TREE -> LEFT)
SET ROOT -> DATA = TEMP -> DATA
Delete(ROOT -> LEFT, TEMP -> DATA)
3/5/2022
VELAMMAL ENGINEERING COLLEGE, Dept. of CSE 72
// node with only one child or no child
ELSE
SET TEMP = ROOT
IF ROOT -> LEFT = NULL AND ROOT->
RIGHT = NULL
SET ROOT = NULL
ELSE IF ROOT -> LEFT != NULL
SET ROOT = ROOT -> LEFT
ELSE
SET ROOT = ROOT -> RIGHT
[END OF IF]
FREE TEMP
[END OF IF]
Step 2: END](https://image.slidesharecdn.com/unitiii-220305070553/85/Unit-III-NON-LINEAR-DATA-STRUCTURES-72-320.jpg)