UnconstrOptim_Eng.pptx

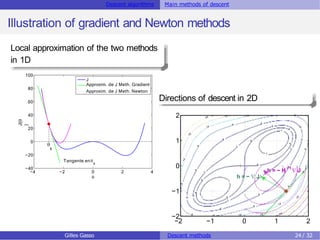
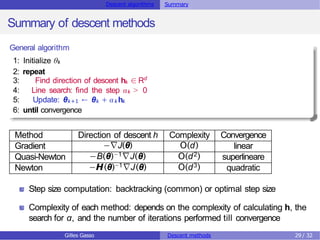
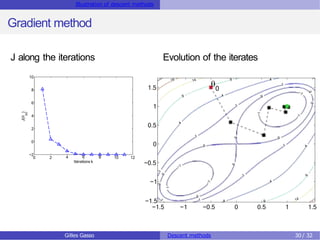
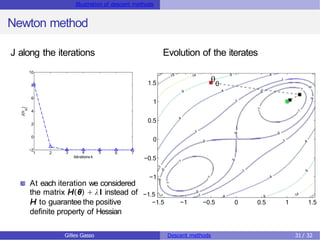
Descent methods
for unconstrained optimization
Gilles Gasso
INSA Rouen
Laboratory LITIS
October 13, 2019
Gilles Gasso Descent methods 1/ 32

Plan
1 Formulation
2 Optimality conditions
3 Notions gradient
Existence of a solution
4 Descent algorithms
Main methodsof descent
Researchof the step
Summary
5 Illustration of descent methods

Formulation
Unconstrained optimization
Elements of the problem
θ ∈Rd : vector of unknown real parameters
J : Rd → R : the function to be minimized.
Assumption: J is differentiable all over its domain
domJ = θ ∈Rd |J(θ) < ∞
}
Problem formulation
(P) min J(θ)
θ∈Rd

Formulation
Unconstrained optimization
Examples
1
J(θ) = θT Pθ + qT θ + r
2
with P a positive definite matrix
−1
0
1
2
−2 −2
0
4
2
4.5
5
5.5
6

1

2
J()
0
2
4
6
0
2
4
−2
6
2
1
J
θ
(θ) = cos(θ −θ)+sin(θ +θ )+ 1
0
1 2 1 2
4
−1

Optimality conditions
Different solutions
Global solution
θ∗ is said to be the global minimum solution of the problem if
J(θ∗) ≤ J(θ), ∀
θ ∈domJ
Local solution
θ
ˆis a local minimum solution of problem (P) if it holds
J(θ̂) ≤ J(θ), ∀
θ ∈domJ such that ǁθ̂ −θǁ ≤ ϵ, ϵ > 0
Illustration
J(θ) = cos(θ1 2
—θ ) + sin 1 2
(θ + θ ) + θ1
4
0 1 2 3 4 5
0
1
2
3
4
5
*

Minimum global
Minimumlocal
−1
−0.5
0
0.5
1
1.5
2
2.5

How do we assess a solution to the problem?

Notions gradient
Differentiability
What for?
Differentiability allows to checkif aθ is solution
Allows to get a local linear approximation of J
Notion of gradient
Let J : Rd → R beadifferentiable function allover its domain. The
gradient of J at θ ∈domJ is the d-dimensional vector denoted as ∇J(θ)
and defined as
∇J(θ) = ∂J(θ)
∂θ1
··· ∂J(θ)
∂θd
T
∂θk
∂J(θ)
is the partial derivative of J w.r.t. parameter θk.

Notions gradient
Example
4 4
1 2
J(θ) = θ + θ −4θ θ
1 2
Gradient: ∇J(θ) =
3
1
4θ −4θ2
−4θ1 + 4θ3
2
Evaluation at θ =
1
−1
: ∇J(θ) =
8
−8
Exercise
1 2
Find the gradient function of J(θ) = cos(θ −θ ) + sin 1 2
(θ + θ ) + θ1
4

Notions gradient
Gradient calculation
t→ 0
Gateaux directional derivative
Let the function J : Rd → R and let h ∈Rd beavector. The Gateaux
directional derivative of J at θ ∈Rd along the direction h is the limit (if it
exists)
D(h, θ) = lim
J(θ + th) −J(θ)
t
the gradient
Let J : Rd → R adifferentiable function at θ ∈Rd . The gradient of J at θ is the
unique vector ∇J(θ) ∈ Rd such that the directional derivative is the linear form:
D(h, θ) = lim
t→0
J(θ + th) −J(θ)
t
= ∇J(θ)T h

Notions gradient
Examples
Computing the directional derivative in practice
Let be the function φ(t) = J(θ + th) with t ∈R, h ∈Rd , θ ∈ Rd
φ′(0), derivative of φ(t) at t = 0 defines the directional derivative
′
Proof φ (0) = limt→0 = limt→0
φ(t)− φ(0) J(θ+th)− J(θ)
t t
Exercises:from the directional derivative D(h, θ) to the gradient
Compute the gradient of the following functions
Linear function: J(θ) = cT θ with c, θ ∈Rd
Quadratic function: J(θ) = θT
Aθ with A ∈ Rd×d
Gilles Gasso Descent methods 10 / 32

Notions gradient Existence of a solution
Existence of a solution
Theorem
AssumeJ : Rd → R is aproper,continuous and coercicea function. There
the optimization problem minθ J(θ) admits a global solution.
a
the function J is coercive if J(θ) → ∞ for any θ such that ǁθǁ → ∞
Proof.
J being coercice, we have J(θ) → ∞ for ǁθǁ → ∞. Let θ0 ∈ Rd . There exists ν > 0 such that
ǁθǁ > ν ⇒ J(θ) > J(θ0). This means that there exists ν > 0 such that
J(θ) ≤ J(θ0) ⇒ ǁθǁ ≤ ν. To find a solution, il suffices to restrain the minimization to
d
{θ∈R | ǁ θǁ ≤ ν }
d
, ,
min J(θ). As the set θ ∈ R |ǁθǁ ≤ ν is compact, the problem admits a
global solution using Weierstrass theorem.
Interpretation
the theorem states that if J is bounded from below and the bound is
attained for a finite θ, the minimization problem admits a solution.

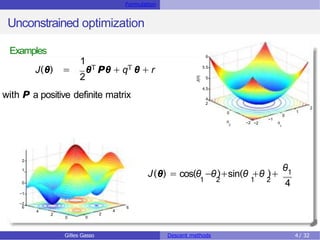
First order necessary condition
Theorem [First order condition]
Let J : Rd → R be a differential function on its domain. A vector θ0 is a
(local or global) solution of the problem (P), if it necessarily satisfies the
condition ∇J(θ0) = 0.
Vocabulary
Any vector θ0 that verifies ∇J(θ0) = 0 is called a stationary point or critical
point
∇J(θ) ∈Rd is the gradient vector of J at θ.
The gradient is the unique vector such that the directional derivative can be
written as:
lim
t→0
J(θ + th) −J(θ)
t
T h
= ∇J(θ) , h ∈Rd, t ∈R

Example of a first order optimality condition
4 4
1 2
J(θ) = θ + θ −4 θ θ
1 2
Gradient ∇J(θ) =
3
1
4θ − 4θ2
−4θ1 + 4θ 3
2
Stationary points that verify ∇J(θ) = 0.
0
(1) (2)
Three solutions θ = , θ =
0 1
1
et
θ(3)
=
−1
−1 −2 −1 0 1 2
−2
−1
0
1
2
Remarks
θ(2) and θ(3) are local minimal but not θ(1)
every stationary point can be deemed a local extremum
We need another optimality condition
How to ensure that a stationary point is a minimum?

Hessian matrix
Twice differential function
J : Rd → R is saidto beatwice differentiable function on its domain
domJ if, at everypoint θ ∈,there existsanunique symmetrical matrix
H(θ) ∈Rd×d called Hessian matrix such that
J(θ + h) = J(θ) + ∇J(θ)T + hTH(θ)h + ǁhǁ2ε(h).
ε(h) is a continuous function at 0 with limh→0 ε(h) = 0
H(θ) is the second derivative matrix
H(θ) =
∂2J ∂2J
∂θ1∂θ1 ∂θ1∂θ2
∂2J
∂θ1∂θd
. . .
.
∂2J
···
. ··· .
∂2J ∂2J
···
∂θd ∂θ1 ∂θd ∂θ2 ∂θd ∂θd
H(θ) = ∇θT(∇θJ(θ)) is the Jacobian of the gradient function

Examples
Example 1
Objective function
4 4
1 2
J(θ) = θ + θ −4θ θ
1 2
Gradient
∇J(θ) =
3
1
4θ −4θ2
3
−4θ1 + 4θ2
Hessian matrix
H(θ) =
12θ2
1
−4
2
−4 12θ2
Exemple 2
Quadratic objective function
J(θ) = 1θT Pθ + qT θ + r
2
Directional derivative
D(h, θ) = limt→ 0
J(θ+th)−J(θ)
t
D(h, θ) = (Pθ + q)T h
Gradient ∇J(θ) = Pθ + q
Hessian matrix H(θ) = P

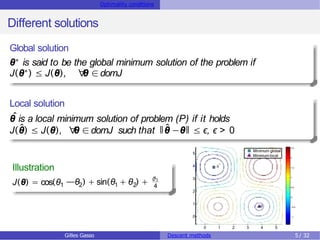
Second order optimality condition
Theorem [Second order optimality condition]
Let J : Rd → R beatwice differentiable function on its domain. If θ0 is a
minimum of J, then ∇J(θ0) = 0 and H(θ0) is a positive definite matrix.
Remarks
H is positive definite if and only if all its eigenvalues are positive
H is negative definite if and only if all its eigenvalues are negative
For θ ∈R, this condition means that the gradient of J at the minimum is
null, J′(θ) = 0 and its second derivative is positive i.e. J′′(θ) > 0
If at a stationary point θ0 H(θ0)) is negative definite, θ0 is a local
maximum of J

Illustration of the second order optimality condition
4 4
1 2
J(θ) = θ + θ −4 θ θ
1 2
Gradient : ∇J(θ) =
3
1
4θ −4θ2
−4θ1 + 4θ3
2
Stationary points : θ(1)
=
0
0
, θ(2)
= 1
1
and
θ(3)
=
−1
−1
Hessian matrix H(θ) =
12θ2
1
−4
2
−4 12θ2
−2 −1 0 1 2
−2
−1
0
1
2
θ(1)
θ(2) θ(3)
0 −4
−4 12
12 −4
−4 12
12 −4
−4 12
Hessian
Eigenvalues 4,−4 8,16 8,16
Type of solution Saddle point Minimum Minimum

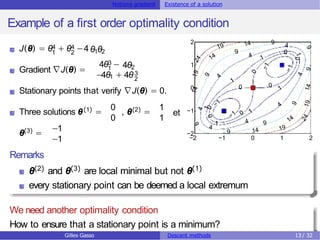
Necessary and sufficient optimality condition
Theorem [2nd order sufficient condition ]
Assumethe hessian matrix H(θ0) of J(θ) at θ0 existsand is positive
definite. Assumealsothe gradient ∇J(θ0) = 0. Then θ0 is a(local or
global) minimum of problem (P).
Theorem [Sufficient and necessary optimality condition]
Let J be a convex function. Every local solution θ
ˆis a global solution θ∗.
Recall
A function J : Rd → R is convex if it verifies
J(αθ + (1−α)z) ≤ αJ(θ) + (1 −α)J(z), ∀
θ, z ∈domJ, 0 ≤ α ≤ 1

How to find the solution(s)?
We have seen how to assessa solution to the problem
A question to be addressed is: how to compute a solution?

Descent algorithms
Principle of descent algorithms
Direction of descent
Let the function J : Rd → R. The vector h ∈Rd is called adirection of
descent in θ if there exists α > 0 such that J(θ + αh) < J(θ)
Principle of descent methods
Start from an initial point θ0
Design a sequence of points { θk} with θk+1 = θk + αk hk
Ensure that the sequence {θk } converges to a stationary point θ
ˆ
hk: direction of descent
αk is the step size

Descent algorithms
General approach
General algorithm
1: Let k = 0, initialize θk
2: repeat
3: Find a descent direction hk ∈Rd
4: Line search: find a step size αk > 0 in the direction hk such that
J(θk + αk hk) decreases "enough"
5: Update: θk+1 ← θk + αk hk and k ← k + 1
6: until ǁ∇J(θk)ǁ < ϵ
The methods of descent differ by the choice of:
h: gradient algorithm, Newton, Quasi-Newton algorithm
α: Line search, backtracking

Descent algorithms Main methods of descent
Gradient Algorithm
Theorem [descent direction and opposite direction of gradient]
Let J(θ) beadifferential function. The direction h = −∇J(θ) ∈Rd is a
descent direction.
Proof.
J being differentiable, for any t > 0 we have
J(θ + th) = J(θ) + t∇J(θ)Th + tǁhǁϵ(th). Setting h = −∇J(θ), we get
J(θ + th) −J(θ) = −tǁ∇J(θ)ǁ2 + tǁhǁϵ(th). For t small enough ϵ(th) → 0 and
so J(θ + th) −J(θ) = −tǁ∇J(θ)ǁ2 < 0. It is then a descent direction.
Characteristics of the gradient algorithm
Choice of the descent direction at θk: hk = −∇J(θk)
Complexity of the update: θk+1 ← θk −αk ∇J(θk) costs O(d)

Newton algorithm
2nd order approximation of the twice diffetentiable J at θk
k k
Th
1
2
k
J(θ + h) ≈ J(θ ) + ∇J(θ ) + hTH(θ )h
with H(θk ) the positive definite Hessian matrix
The direction hk which minimizes this approximation is obtained by
∇J(θ + hk) = 0 ⇒ hk = −H(θk)− 1∇J(θk)
Features
Choice of the descent direction at θk : hk = −H(θk)−1∇J(θk )
Complexity of the update: θk+1 ← θk −αk H(θk )−1∇(θk ) costs
O(d3) flops
H(θk ) is not always guaranteed to be positive definite matrix. Hence
we cannot always ensure that hk is a direction of descent

Illustration of gradient and Newton methods
Local approximation of the two methods
in 1D
−4 −2 2 4
−40
−20
0
20
40
60
80
100
Tangente en
k
0

J(
)

k
J
Approxim. de J Meth. Gradient
Approxim. de J Meth. Newton
Directions of descent in 2D
0
−2 −1 0 1 2
−2
−1
0
1
2
−1
h = − H  J
h = −  J

Quasi-Newton method
Main features
Choiceof the descentdirection at θk : hk = −B(θk )−1∇J(θk )
B(θk ) is an positive definite approximation of the Hessian matrix
Complexity of the update: most of the times O(d2)

Descent algorithms Research of the step
Line search
α>0
Assumethe direction of descenthk at θk is fixed. We aim to find the step
sizeαk > 0 in the direction hk suchthat the function J(θk + αk hk )
decreases enough (compared to J(θk ))
Several options
Fixed step size: use a fixed value α > 0 at each iteration k
θk+1 ← θk + αhk
Optimal step size αk
∗
θk+1 ← θk + αk
∗ hk with αk
∗ = argminJ(θk + αhk )
Variable step size: the choice αk is adapted to the current iteration
θk+1 ← θk + αkhk

Line search
Pros and cons
Fixed step size strategy: often not very effective
Optimal step size: can be costly in calculation time
Variable step: most commonly used approach
The step is often imprecise
A trade-off between computation cost and decrease of J

Variable step sizeh
Armijo’s rule
Determine the step size αk in order to have a sufficient decrease of J i.e.
J(θk + αk h) ≤ J(θk ) + c αk ∇J(θk )T hk
Usually c is chosen in the range 10− , 10−
5 1
Having hk the direction of descent, we have ∇J(θk )Thk < 0, which ensures
the decrease of J
Backtracking
1: Fix an initial step ᾱ, choose 0 < ρ < 1, α ← ᾱ
2: repeat
3: α ← ρα
4: until J(θk + αh) > J(θk ) + c α∇J(θk )T hk
Interpretation: as long as J does not decrease, we
decrease the value of the step size
Choice of the initial step
Newton method:
ᾱ = 1
Gradient method:
ᾱ = 2J(θk )− J(θk− 1)
∇J(θk )T hk

Descent algorithms Summary
Summary of descent methods
General algorithm
1: Initialize θk
2: repeat
3: Find direction of descent hk ∈ Rd
4: Line search: find the step αk > 0
5: Update: θk+1 ← θk + αk hk
6: until convergence
Method Direction of descent h Complexity Convergence
Gradient −∇J(θ) O(d) linear
Quasi-Newton −B(θ)−1∇J(θ) O(d2) superlineare
Newton −H(θ)−1∇J(θ) O(d3) quadratic
Step size computation: backtracking (common) or optimal step size
Complexity of each method: depends on the complexity of calculating h, the
search for α, and the number of iterations performed till convergence

Illustration of descent methods
Gradient method
J along the iterations Evolution of the iterates
0 2 10 12
−2
0
2
4
6
8
10
4 6 8
Itérations k
(k)
J(
)

0
−1.5 −1 −0.5 0 0.5 1 1.5
−1
−1.5
−0.5
0
0.5
1
1.5

Newton method
J along the iterations Evolution of the iterates
1 2 6 7
−2
0
2
4
6
8
10
3 4 5
Itérations k
(k)
J(
)
H to guarantee the positive
definite property of Hessian

0
−1.5 −1 −0.5 0 0.5 1 1.5
At each iteration we considered
the matrix H(θ) + λ I instead of −1.5
−1
−0.5
0
0.5
1
1.5

Conclusion
Unconstrained optimization of smooth objective function
Characterization of the solution(s) requires checking the optimality
conditions
Computation of a solution using descent methods
Gradient descent method
Newton method
Not covered in this lecture:
Convergence analysis of the studied algorithms
Non-smooth optimization
Gradient-free optimzation

UnconstrOptim_Eng.pptx

More Related Content

Similar to UnconstrOptim_Eng.pptx

Recently uploaded

UnconstrOptim_Eng.pptx