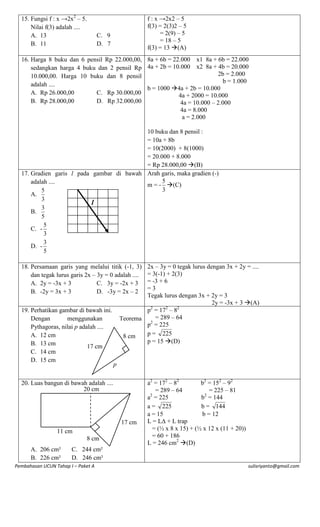
Dokumen ini terdiri dari pembahasan soal-soal ujian tahap I paket A, yang mencakup berbagai topik matematika seperti operasi aritmatika, persentase, geometri, dan analisis fungsi. Beberapa contoh soal meliputi perhitungan uang, penggunaan rumus geometri untuk menghitung luas, serta soal tentang aturan himpunan dan fungsi. Total terdapat 30 soal dengan jawaban yang sudah disediakan untuk setiap pertanyaan.

1. PEMBAHASAN SOAL UCUN TAHAP I – PAKET A
1. Hasil dari : -72 + 56 : (-8) = ....
A. -79
C. 2
B. -2
D. 79
-72 + 56 : (-8)
= -72 + (-7)
= -79  (A)
2. Lia akan membeli sepeda namun uangnya
tidak cukup. Untuk itu, ayahnya memberi
1
dari uang yang dimiliki Lia, Ibu memberi
2
2
,
sedangkan
kakaknya
memberi
5
1
1 bagian dari uang yang dimiliki Lia.
4
Akhirnya uang yang dimiliki Lia saat ini
adalah Rp 2.150.000,00. Maka uang Lia
mula-mula adalah ....
A. Rp 600.000,00
B. Rp 750.000,00
C. Rp 900.000,00
D. Rp 1.000.000,00
3. Sebuah kendaraan bermotor menghabiskan
6 liter bensin untuk menempuh jarak 240
km. Berapa liter bensin yang diperlukan
kendaraan tersebut untuk menempuh jarak
360 km ?
A. 10 liter
C. 8 liter
B. 9 liter
D. 4 liter
Misal uang Lia = L
1
2
1
L + L + 1 L + L = 2.150.000
2
5
4
1
2
5
L + L + L + L = 2.150.000
2
5
4
10
8
25
20
L+
L+
L+
L = 2.150.000
20
20
20
20
63
L = 2.150.000
20
20
L = 2.150.000 x
63
L = Rp 682.539,68 (ANULIR)
2
2
5. Bentuk sederhana dari 12 x
360
x 6 liter
240
= 9 liter (B)
a=
2
27 3 = (33 ) 3
= 32
= 9 (A)
4. Nilai dari 27 3 adalah ....
A. 9
C. 3
B. 6
D. 2
6 = ....
A. 10 8
C. 6 3
B. 9 2
D. 6 2
6. Hasna menabung di Bank sebesar Rp
5.000.000,00 besar bunga yang diberikan
oleh bank adalah 20% per tahun. Besar
tabungan Hasna setelah menabung Hasna 9
bulan adalah ....
A. Rp 5.450.000,00
B. Rp 5.500.000,00
C. Rp 5.550.000,00
D. Rp 5.750.000,00
7. Barisan geometri suku ke-2 = 4 dan suku
ke-4 = 64. Suku ke-7 dari barisan adalah ...
A. 512
C. 2.048
B. 1.024
D. 4.096
Pembahasan UCUN Tahap I – Paket A
6 liter 240 km
a 360 km
12 x
6=
72
= 36.2
= 6 2 (D)
9
20
x
x Rp 5.000.000,00
12 100
= Rp 750.000,00
Tabungan Hasna = Rp 5.000.000 + Rp 750.000
= Rp 5.750.000,00 (D)
Bunga 9 bulan =
U2 = 4, U4 = 64
Manual :
...., 4, ...., 64, ..... dikali 4
Barisannya menjadi :
1, 4, 16, 64, 256, 1024, 4096 (D)
sulisriyanto@gmail.com

2. 8. Sebuah percobaan menunjukkan bahwa
satu bakteri dapat membelah diri menjadi 4
bakteri dalam waktu 30 menit. Jika dalam
sebuah tabung terdapat 6 bakteri, maka
jumlah bakteri setelah 2 jam adalah ....
A. 96
C. 384
B. 256
D. 1.536
2 jam = 120 menit
Sehingga :
0 30 60 90 120
6...24...96...384...1536 (D)
9. Di ruang seminar terdapat 15 baris kursi,
diatur dengan selalu menambah 2 kursi
pada baris berikutnya. Jika pada baris
terdepan terdapat 8 kursi, maka banyak
kursi pada baris terakhir adalah ....
A. 46
C. 38
B. 44
D. 36
2
10. Pemfaktoran dari 36x – 9y2 adalah ....
A. (6x + 3y)(6x – 3y)
B. (6x – 3y)(6x – 3y)
C. (4x + 3y)(9x – 3y)
D. (4x – 3y)(6x – 3y)
2
1
11. Dari penyelesaian :
x + 2 =
x + 3,
4
3
maka nilai x + 3 adalah ....
A. 9
C. 15
B. 12
D. 18
Un = a + (n – 1)b
U15 = 8 + (15 – 1)2
= 8 + 28
U15 = 36 (D)
36x2 – 9y2 = (6x + 3y)(6x – 3y) (A)
2
1
x+2= x+3
3
4
(dikalikan 12)
8x + 24 = 3x + 36
8x – 3x = 36 – 24
Nilai x + 3 = 2,4 + 3
5x = 12
= 5,4 (ANULIR)
12
x=
5
x = 2,4
12. Jika P = {x| 3 < x ≤ 14, x bilangan cacah} P = {x| 3 < x ≤ 14, x bilangan cacah} P = {4, 5, 6, ...,
dan Q = {x| 6 ≤ x < 11, x bilangan cacah}, 14}
Q = {x| 6 ≤ x < 11, x bilangan cacah} Q = {6, 7, 8, 9,
maka P  Q adalah ....
10}
A. {6, 7, 8, 9, 10}
P  Q = {6, 7, 8, 9, 10} (A)
B. {4, 5, 6, 7, 8, 9, 10}
C. {4, 5, 11, 12, 13, 14}
D. {3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
13. Dari sekelompok siswa, tercatat 18 orang n(A  B) = n(A) + n(B) – n(A  B)
= 18 + 15 – 8
suka menonton pertunjukkan musik, 15
n(A  B) = 25
orang suka menonton pertandingan
n(S) = 25 + 2
olahraga, 8 orang suka menonton
= 27 (D)
pertunjukan musik dan pertandingan
olahraga dan 2 orang tidak suka kedua
kegiatan tersebut. Banyaknya siswa dalam
kelompok adalah ....
A. 43 orang
C. 35 orang
B. 39 orang
D. 27 orang
14. Perhatikan himpunan pasangan berurutan Daerah asal hanya dipetakan satu kali.
Yang merupakan fungsi :
berikut ini !
ii. {(a, 1), (b, 1), (c, 1), (d, 1)} dan
I.
{(a, 1), (a, 2), (a, 3), (a, 4)}
iii.{(b, 1), (a, 2), (d, 3), (c, 4)} (ii) dan (iii) (B)
II.
{(a, 1), (b, 1), (c, 1), (d, 1)}
III.
{(b, 1), (a, 2), (d, 3), (c, 4)}
IV.
{(a, 1), (a, 2), (b, 3), (b, 4)}
Yang merupakan pemetaan adalah ....
A. I dan II
C. I dan IV
B. II dan III
D. III dan IV
Pembahasan UCUN Tahap I – Paket A
sulisriyanto@gmail.com

3. 15. Fungsi f : x →2x2 – 5.
Nilai f(3) adalah ....
A. 13
B. 11
f : x →2x2 – 5
f(3) = 2(3)2 – 5
= 2(9) – 5
= 18 – 5
f(3) = 13 (A)
C. 9
D. 7
16. Harga 8 buku dan 6 pensil Rp 22.000,00, 8a + 6b = 22.000 x1 8a + 6b = 22.000
sedangkan harga 4 buku dan 2 pensil Rp 4a + 2b = 10.000 x2 8a + 4b = 20.000
2b = 2.000
10.000,00. Harga 10 buku dan 8 pensil
b = 1.000
adalah ....
b = 1000 4a + 2b = 10.000
A. Rp 26.000,00
C. Rp 30.000,00
4a + 2000 = 10.000
B. Rp 28.000,00
D. Rp 32.000,00
4a = 10.000 – 2.000
4a = 8.000
a = 2.000
10 buku dan 8 pensil :
= 10a + 8b
= 10(2000) + 8(1000)
= 20.000 + 8.000
= Rp 28.000,00 (B)
17. Gradien garis l pada gambar di bawah Arah garis, maka gradien (-)
5
adalah ....
m = - (C)
3
5
A.
3
l
3
B.
5
5
C. 3
3
D. 5
2x – 3y = 0 tegak lurus dengan 3x + 2y = ....
= 3(-1) + 2(3)
= -3 + 6
=3
Tegak lurus dengan 3x + 2y = 3
2y = -3x + 3 (A)
2
2
2
p = 17 – 8
= 289 – 64
Teorema
2
p = 225
p = 225
8 cm
p = 15 (D)
18. Persamaan garis yang melalui titik (-1, 3)
dan tegak lurus garis 2x – 3y = 0 adalah ....
A. 2y = -3x + 3
C. 3y = -2x + 3
B. -2y = 3x + 3
D. -3y = 2x – 2
19. Perhatikan gambar di bawah ini.
Dengan
menggunakan
Pythagoras, nilai p adalah ....
A. 12 cm
B. 13 cm
17 cm
C. 14 cm
D. 15 cm
p
20. Luas bangun di bawah adalah ....
20 cm
17 cm
11 cm
8 cm
A. 206 cm²
B. 226 cm²
a2 = 172 – 82
b2 = 152 – 92
= 289 – 64
= 225 – 81
a2 = 225
b2 = 144
a = 225
b = 144
a = 15
b = 12
L = L∆ + L trap
= (½ x 8 x 15) + (½ x 12 x (11 + 20))
= 60 + 186
L = 246 cm2 (D)
C. 244 cm²
D. 246 cm²
Pembahasan UCUN Tahap I – Paket A
sulisriyanto@gmail.com

4. ½ d1 = ½ (16) = 8 cm
½ d2 = ½ (30) = 15 cm
s2 = 152 + 82
= 225 + 64
s2 = 289
s = 289
s = 17
22. Diketahui besar sudut P = (3x – 9)° dan  P +  Q = 90
sudut Q = (2x + 4)°. Jika kedua sudut saling 3x – 9 + 2x + 4 = 90
5x – 5 = 90
berpenyiku, maka besar sudut P adalah ....
5x = 90 – 5
A. 48°
C. 38°
5x = 85
B. 42°
D. 32°
x = 17
21. Sebuah taman berbentuk belahketupat yang
panjang diagonalnya 16 cm dan 30 cm.
Keliling taman tersebut adalah ....
A. 46 cm
C. 68 cm
B. 63 cm
D. 94 cm
K = 4s
= 4(17)
= 68 cm (C)
 P = 3x – 9
= 3(17) – 9
= 51 – 9
 P = 42° (B)
23. Perhatikan gambar berikut !
AE DE

Segitiga ABC sebangun dengan segitiga AB BC
6
4
ADE dan ED//BC, maka panjang AB

adalah ....
AB 12
C
4AB = 72
A. 12 cm
AB = 18 cm (D)
D
B. 14 cm 12 cm
C. 16 cm
4 cm
D. 18 cm
6 cm
E
A
B
24. Sebuah tiang yang tingginya 4 m 4 5

mempunyai bayangan 5 m. Pada saat yang 16 a
sama, pohon yang tingginya 16 m akan 4a = 80
a = 20 m (B)
mempunyai bayangan ....
A. 18 m
C. 23 m
B. 20 m
D. 24 m
25. Perhatikan gambar !
D
AC = CE
 ACB =  DCE
BC = CD
Syarat : sisi, sudut, sisi (B)
E
C
A
B
Syarat yang menunjukkan bahwa ∆ABC
kongruen dengan ∆CDE adalah ....
A. Sisi, sisi, sisi
B. Sisi, sudut, sisi
C. sudut, sisi, sudut
D. sudut, sudut, sudut
Cara jelas
26. Perhatikan gambar di bawah ini !
Garis bagi adalah AD (B)
Yang merupakan garis berat adalah ....
A. Garis AC
C
B. Garis AD
C. Garis BF
D
D. Garis CE
F
°
A
°
E
Pembahasan UCUN Tahap I – Paket A
B
sulisriyanto@gmail.com

5. 27. Perhatikan gambar di bawah !
Titik O merupakan pusat lingkaran.
Jika  BOC +  BAC = 150°,
maka  BDC +  BEC = ....
D
A. 80°
B. 90°
C. 100°
A
E
D. 120°
O
B
 BOC adalah sudut pusat
 BAC adalah sudut keliling
Sudut pusat besarnya dua kali sudut keliling
Sehingga :
 BOC +  BAC = 150°
2  BAC +  BAC = 150°
3  BAC = 150°
 BAC = 50°
 BDC =  BEC = 50°
Maka :  BDC +  BEC = 50 + 50
= 100° (C)
C
28. Panjang garis singgung persekutuan luar
dua lingkaran 24 cm. Jika panjang jari-jari
masing-masing lingkaran adalah 15 cm dan
5 cm, maka jarak pusat kedua lingkaran
adalah ....
A. 25 cm
C. 27 cm
B. 26 cm
D. 28 cm
29. Banyak sisi dan rusuk pada limas segi lima
adalah ....
A. 5 dan 8
C. 6 dan 10
B. 5 dan 10
D. 6 dan 12
Gl2 = AB2 – (R – r)2
242 = AB2 – (15 – 5)2
576 = AB2 – 100
AB2 = 576 + 100
AB2 = 676
AB = 576
AB = 26 cm (B)
30. Perhatikan gambar !
(i)
Cara jelas
Merupakan juring adalah (ii) dan (iii) (B)
(iii)
(ii)
Limas segitima
Banyak sisi = n + 1
Banyak rusuk = 2n
=5+1
= 2(5)
=6
= 10
Banyak sisi dan rusuk adalh 6 dan 10 (C)
(iv)
Gambar yang merupakan jaring-jaring
balok adalah ....
A. i dan ii
C. ii dan iii
B. i dan iii
D. ii dan iv
31. Sebuah limas dengan alas berbentuk V limas = ⅓ x La x t
= ⅓ x ½ x d1 x d2 x t
belahketupat.
Jika
panjang
kedua
= ⅓ x ½ x 16 x 12 x 24
diagonalnya 16 cm dan 12 cm serta tinggi
V limas = 768 cm³ (D)
24 cm, maka volume limas adalah ....
A. 2.304 cm³
C. 1.152 cm³
B. 1.536 cm³
D. 768 cm³
Pembahasan UCUN Tahap I – Paket A
sulisriyanto@gmail.com

6. 32. Pada gambar di bawah, sebuah benda Tinggi tabung = 34 – 24
= 10 cm
berbentuk tabung dan kerucut dengan jariV benda = V tabung + V kerucut
jari 10 cm. Jika tinggi kerucut 24 cm, maka
= πr²t1 + ⅓πr²t2
volume benda adalah ....
= πr² (t1 + ⅓t2)
A. 6.552 cm³
= 3,14 x 10 x 10 x (10 + 8)
B. 5.652 cm³
= 314 x 18
C. 5.562 cm³
V benda = 5.652 cm³ (B)
D. 5.526 cm³
34 cm
33. Bak penampung air berbentuk tabung V tabung = πr²t
22
berdiameter 10 m dengan tinggi 7 m.
=
x5x5x7
7
Volume bak jika terisi penuh adalah ....
= 550 m³
A. 1.100.00 liter
C. 55.000 liter
V tabung = 550.000 liter (B)
B. 550.000 liter
D. 22.000 liter
34. Sebuah prisma dengan alas
kaki panjang sisinya 10 cm,
dan tinggi prisma 50 cm.
permukaan prisma adalah ....
A. 1.920 cm²
C.
B. 1.290 cm²
D.
segitiga sama Tinggi segitiga :
2
2
2
13 cm, 13 cm t = 13 – 5
Luas seluruh 2 = 169 – 25
t = 144
t = 144
960 cm²
t = 12 cm
645 cm²
Lp prisma = 2La + Ka.tp
= (2 x ½ x 10 x 12) + (10 + 13 + 13).50
= 120 + 1.800
Lp = 1.920 cm² (A)
35. Diketahui belahan bola padat dengan jari- Lp = 3πr²
= 3 x 3,14 x 20 x 20
jari 20 cm seperti gambar. Luas belahan
= 3.768 cm² (C)
bola tersebut adalah ....
A.
B.
C.
D.
1.256 cm²
2.512 cm²
3.768 cm²
5.024 cm²
36. Hasil ulangan matematika Cony dalam satu
semester adalah 6, 7, 6, 7, 9, 8, 9, 8, 6.
Median dan modus berturut-turut dari data
tersebut adalah ....
A. 7 dan 6
C. 9 dan 8
B. 6 dan 7
D. 8 dan 9
Data urut : 6, 6, 6, 7, 7, 8, 8, 9, 9
Median = 7
Modus = 6
Median dan modus adalah 7 dan 6 (A)
37. Rata-rata berat badan 5 orang anak adalah Berat badan seluruhnya = 6 x 36 = 216
35 kg. Setelah seorang anak masuk dalam Berat badan sebelumnya = 5 x 35 = 175
kelompok tersebut, rata-ratanya menjadi 36
Berat yang masuk = 216 – 175
kg. Berat badan anak yang baru masuk
= 41 kg (B)
adalah ....
A. 65 kg
C. 30 kg
B. 41 kg
D. 15 kg
Pembahasan UCUN Tahap I – Paket A
sulisriyanto@gmail.com

7. 38. Diagram garis berikut menunjukkan hasil
(6x4)  (7x2)  (8x8)  (9x6)
Rata-rata =
uji coba matematika.
4 286
24  14  64  54
=
9
F
20
8
●
r
156
7
=
e
20
6
●
k
= 7,8 (C)
5
u
4
●
e
3
n
2
●
s
1
i
0●
6
7
8
9
Nilai
Nilai rata-ratanya adalah ....
A. 6,75
C. 7,80
B. 7,00
D. 8,60
39. Pada pelambungan dua buah dadu, peluang Dua dadu n(S) = 36
munculnya mata dadu berjumlah 10 adalah Jumlah 10 = (4,6), (5,5), (6,4) n(jumlah 10) = 3
3
....
P(jumlah 10) =
36
1
1
A.
C.
1
12
36
=
(C)
12
1
1
B.
D.
18
9
40. Sebuah kantong berisi 5 bola warna merah, n(S) = 5 + 6 + 9 = 20
6 bola warna biru dan 9 bola warna kuning. n(biru) = 6
Jika dilakukan satu kali pengambilan, maka P(biru) = 6
20
peluang terambilnya bola warna biru adalah
3
....
=
(A)
10
3
1
A.
C.
10
20
3
1
B.
D.
7
6
Pembahasan UCUN Tahap I – Paket A
sulisriyanto@gmail.com