Georg Cantor developed set theory in the late 1800s. He proved that there is no bijection between the natural numbers and the real numbers, showing that some infinities are larger than others. This became known as Cantor's theorem. Cantor also proved the Cantor-Bernstein-Schroeder theorem, which states that if there are injections from set A to B and from B to A, then there is a bijection between A and B, so the sets have the same cardinality. Cantor's work revolutionized mathematics and established set theory as an important field of study.

1. A
2008
A

2. “ "
Georg Cantor:
1845-1918
A

3. Cantor
2
A

4. Cantor ( )
(1777-1855)
I protest above all against the use of an infinite quantity as
a completed one which in mathematics is never allowed.
The infinite is only a manner of speaking in which one
properly speaks of limits.
A

5. Cantor
(1873)
(1873)
A

6. 1873
1874
1891
A

7. CBS Theorem
Outline
1
CBS Theorem
2
A

8. CBS Theorem
A

9. CBS Theorem
( )
( )
A B A ≈ B, A B
A

10. CBS Theorem
( )
( )
A ( ) |A|, A |A| = |B|
A ≈ B.
A

11. CBS Theorem
( )
A |A| = |N|. A
A
A

12. CBS Theorem
Outline
1
CBS Theorem
2
A

13. CBS Theorem
Cantor-Bernstein-Shröder Theorem
(C ANTOR -B ERNSTEIN -S CHRÖDER T HEOREM)
A, B f :A→B g:B→A
f g h : A → B.
A

14. CBS Theorem
CBS
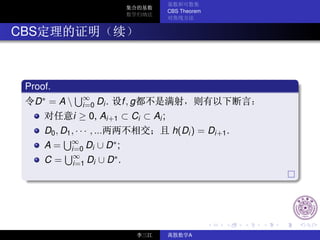
Proof.
C = g[B], h = g ◦ f . Ai , Ci , Di
A0 = A, C0 = C, D0 = A0 C0 ;
An+1 = h[An ], Cn+1 = h[Cn ], Dn+1 = An+1 Cn+1 .
A

15. CBS Theorem
CBS
Proof.
∞
D∗ = A i=0 Di . f,g
i ≥ 0, Ai+1 ⊂ Ci ⊂ Ai ;
D0 , D1 , · · · , ... h(Di ) = Di+1 .
∞ ∗
A= i=0 Di ∪ D ;
∞ ∗
C= i=1 Di ∪ D .
A

16. CBS Theorem
CBS
Proof.
k :A→C
h(a), a ∈ ∞ Di
i=0
f (a) =
a, otherwise.
k A C C B A B
A

17. CBS Theorem
Outline
1
CBS Theorem
2
A

18. CBS Theorem
(1891)
A A
A
A

19. CBS Theorem
A = {♣, ♦, ♥, ♠}
A
♣ ♦ ♥ ♠
{♦, ♥} {♦, ♠} {♣, ♦, ♥} {♣, ♥, ♠}
A

20. CBS Theorem
+
−.
♣ ♦ ♥ ♠
♣ − + + ♣ ♦ ♥ ♠
♦ + ⊕ + −
♥ + − ⊕ + {♦, ♥} {♦, ♠} {♣, ♦, ♥} {♣, ♥, ♠}
♠ − + − ⊕
A

21. CBS Theorem
4
T:
T
T = {♣}.
A
A

22. CBS Theorem
f N
1 2 3 4 ···
···
M1 M2 M3 M4 ···
f f i Mj
(i, j) − +.
M = {i : i ∈ Mi }.
M = Mn n f
A

23. P P n
P(n) P
(i) ( ) P(0)
(ii) ( ) n P(n) P(n + 1) 1
1
P(n)
A

24. (ii)
(ii ) n P(0), P(1), · · · , P(n) P(n + 1)
(1)+(ii )
P P
(ii ) n P(m) m<n P(n)
A

25. “ n, n2 + 5n + 1 "
P “n2 + 5n + 1 " P(n)
P(n + 1)
Proof.
P(n) n2 + 5n + 1
(n + 1)2 + 5(n + 1) + 1 = (n2 + 5n + 1) + 2(n + 3)
(n + 1)2 + 5(n + 1) + 1 P(n + 1)
A

26. P,
A