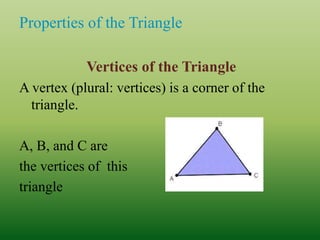
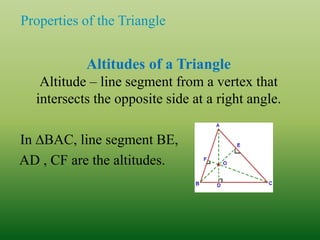
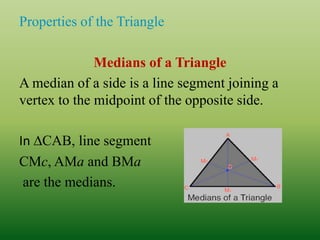
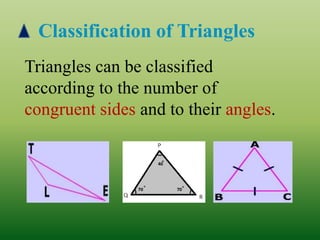
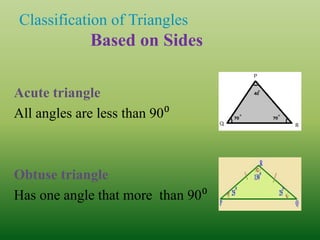
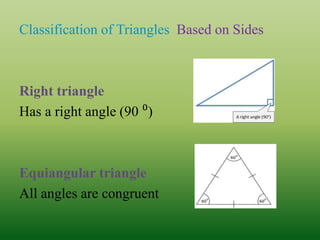
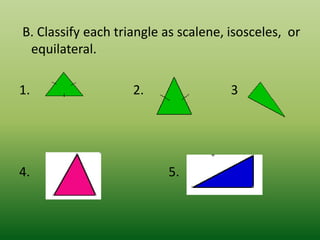
This document defines and classifies different types of triangles based on their sides and angles. It begins by defining what a triangle is and listing some key properties, such as all triangles having three vertices, altitudes, medians, and angle bisectors. The document then classifies triangles as either acute, obtuse, right, equiangular, scalene, isosceles, or equilateral depending on the measurements of their sides and angles. Real-world examples of triangles are also provided. The document concludes with evaluation questions to test the reader's understanding of triangle properties and classifications.

1. TRIANGLES
prepared by: wilton,
harlene, &
concha

2. Objectives
 I can classify different kinds of triangle
according to its sides and angles.
 I can relate the properties and different
kinds of triangle into real life situation.
 I can construct a triangle right
measurements

3. Triangle
A triangle is derived from a Latin word:
tri- "three" and angulus "corner, angle ".
It is a closed figure consisting
of three line segments linked
end-to-end and a
three-sided polygon.

4. Properties of the Triangle
Every triangle has
three vertices
three altitudes,
three medians, and
three angle bisectors.

5. Properties of the Triangle
Vertices of the Triangle
A vertex (plural: vertices) is a corner of the
triangle.
A, B, and C are
the vertices of this
triangle

6. Properties of the Triangle
Altitudes of a Triangle
Altitude – line segment from a vertex that
intersects the opposite side at a right angle.
In ∆BAC, line segment BE,
AD , CF are the altitudes.

7. Properties of the Triangle
Medians of a Triangle
A median of a side is a line segment joining a
vertex to the midpoint of the opposite side.
In ∆CAB, line segment
CMc, AMa and BMa
are the medians.

8. Properties of the Triangle
Angle Bisector of the Triangle
An angle bisector divides an angle into two
congruent angles.
In ∆DEF, line EG is angle
bisector of. angle E

9. Classification of Triangles
Triangles can be classified
according to the number of
congruent sides and to their angles.

10. Classification of Triangles
Based on Sides
Acute triangle
All angles are less than 90⁰
Obtuse triangle
Has one angle that more than 90⁰

11. Classification of Triangles Based on Sides
Right triangle
Has a right angle (90 ⁰)
Equiangular triangle
All angles are congruent

12. Classification of Triangles
Based on Angles
Scalene triangle
No two sides are congruent.
Equilateral triangle
Three sides are congruent.

13. Classification of Triangles Based on Angles
Isosceles triangle
At least two sides are congruent.
The two congruent sides of an isosceles triangle
are called legs.
The third side is called the base.

14. Triangles Around Us

15. Evaluation
A. Determine whether the statement is true or false. If
false, give your reason.
1. A right triangle can be an isosceles triangle.
2. The three sides of a triangle measure 8 cm, 9 cm,
and 10 cm, respectively. The triangle is an isosceles
triangle.
3. If the three angles of a triangle measures 60° each,
the triangle is an acute triangle.
4. All angles of a scalene triangle are acute triangle.
5. All angles of an isosceles triangle are acute angles.

16. B. Classify each triangle as scalene, isosceles, or
equilateral.
1. 2. 3
4. 5.

17. Reference:
Dilao, Soledad J. and Julieta G. Bernabe.
Geometry,Revised Edition, Quezon
City:SD Publications,Inc.,2009.