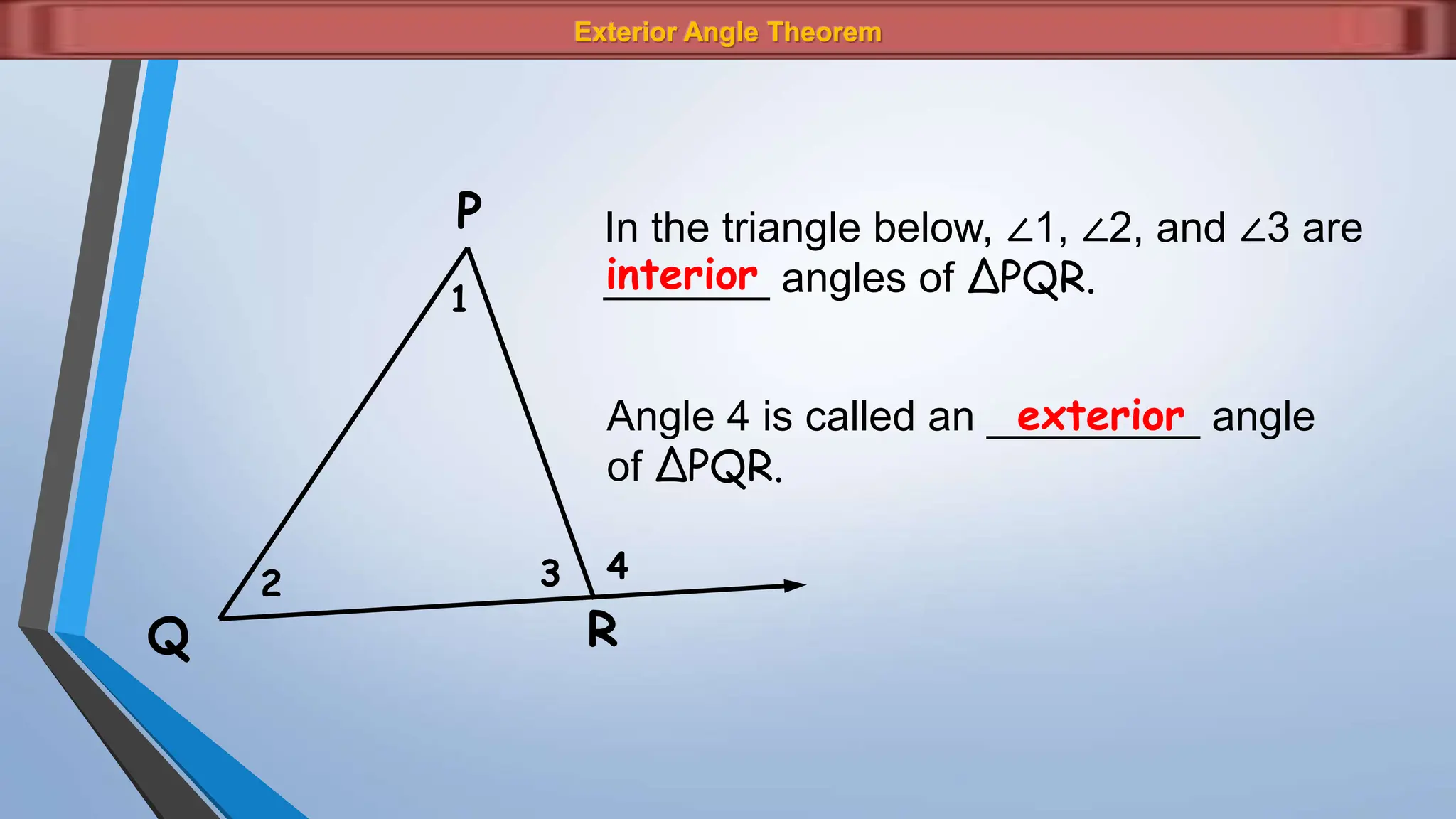
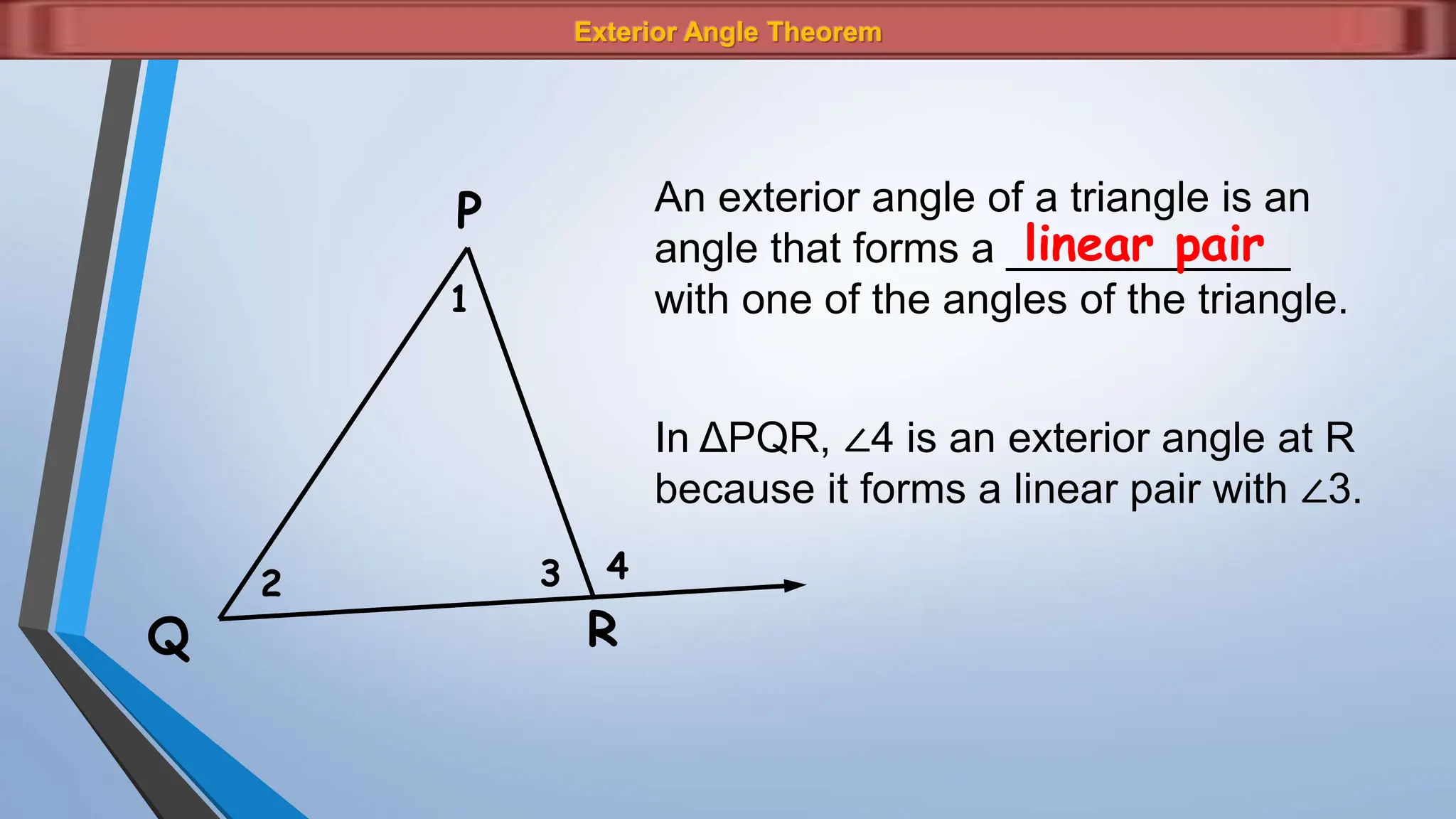
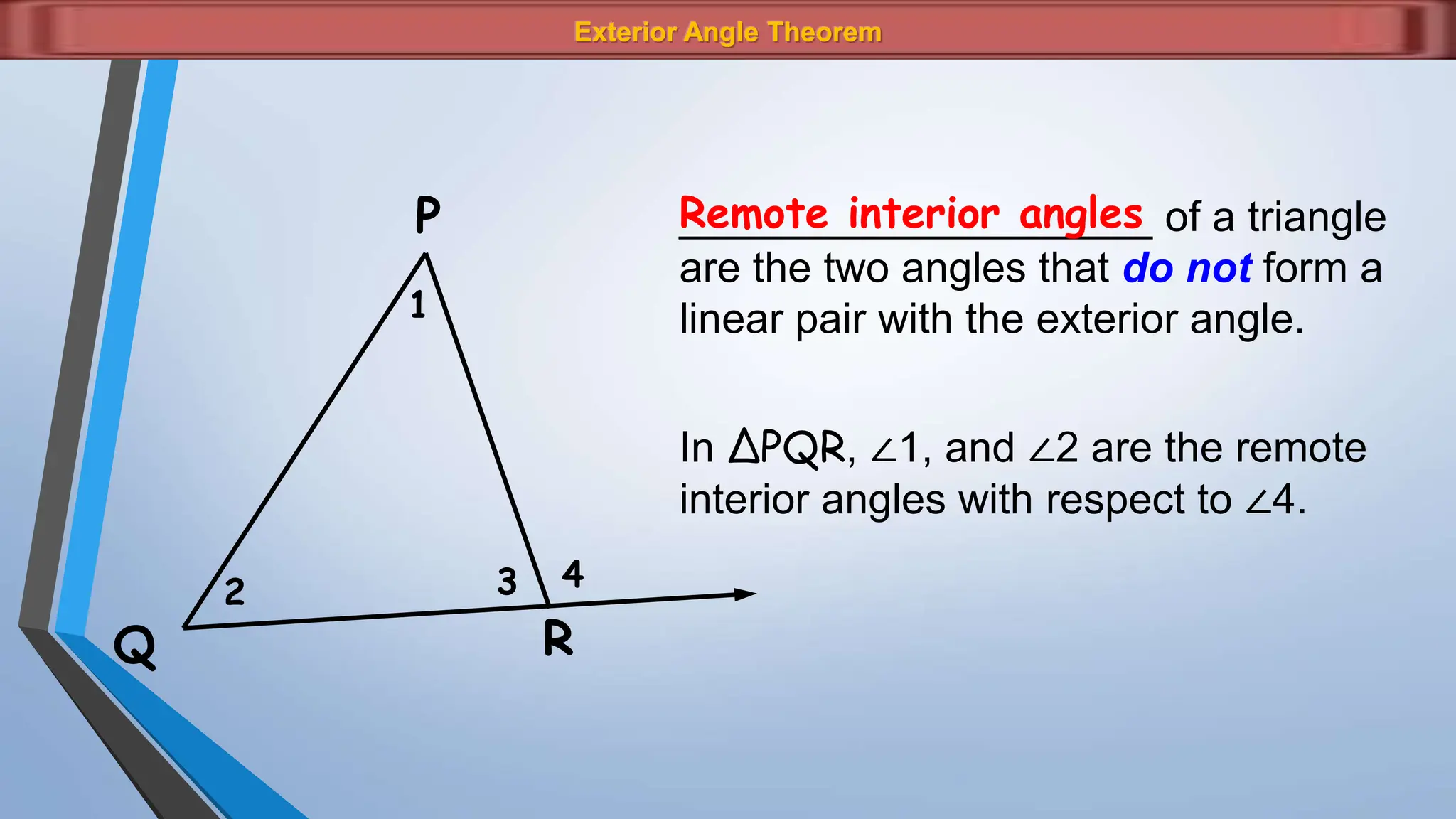
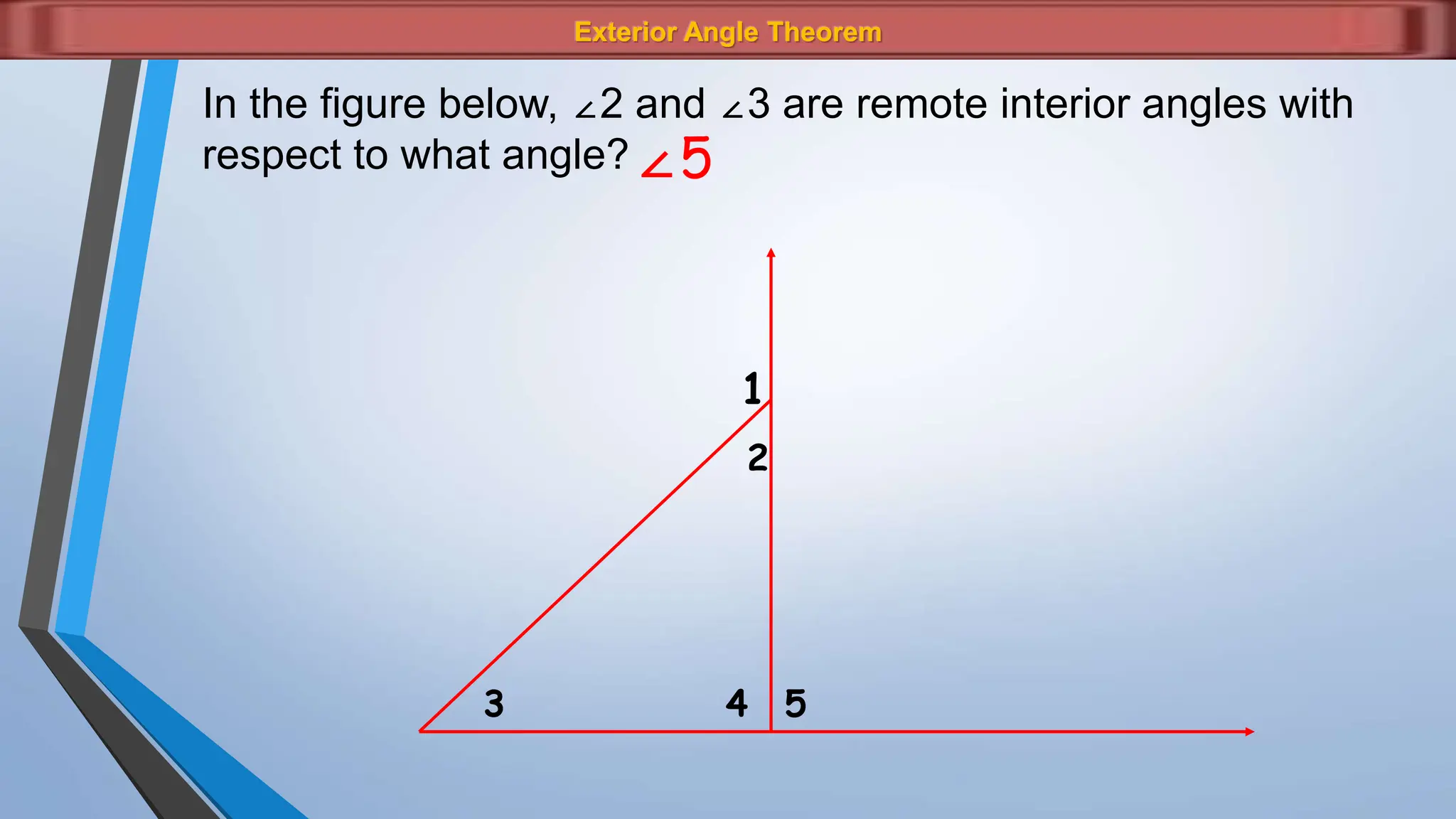
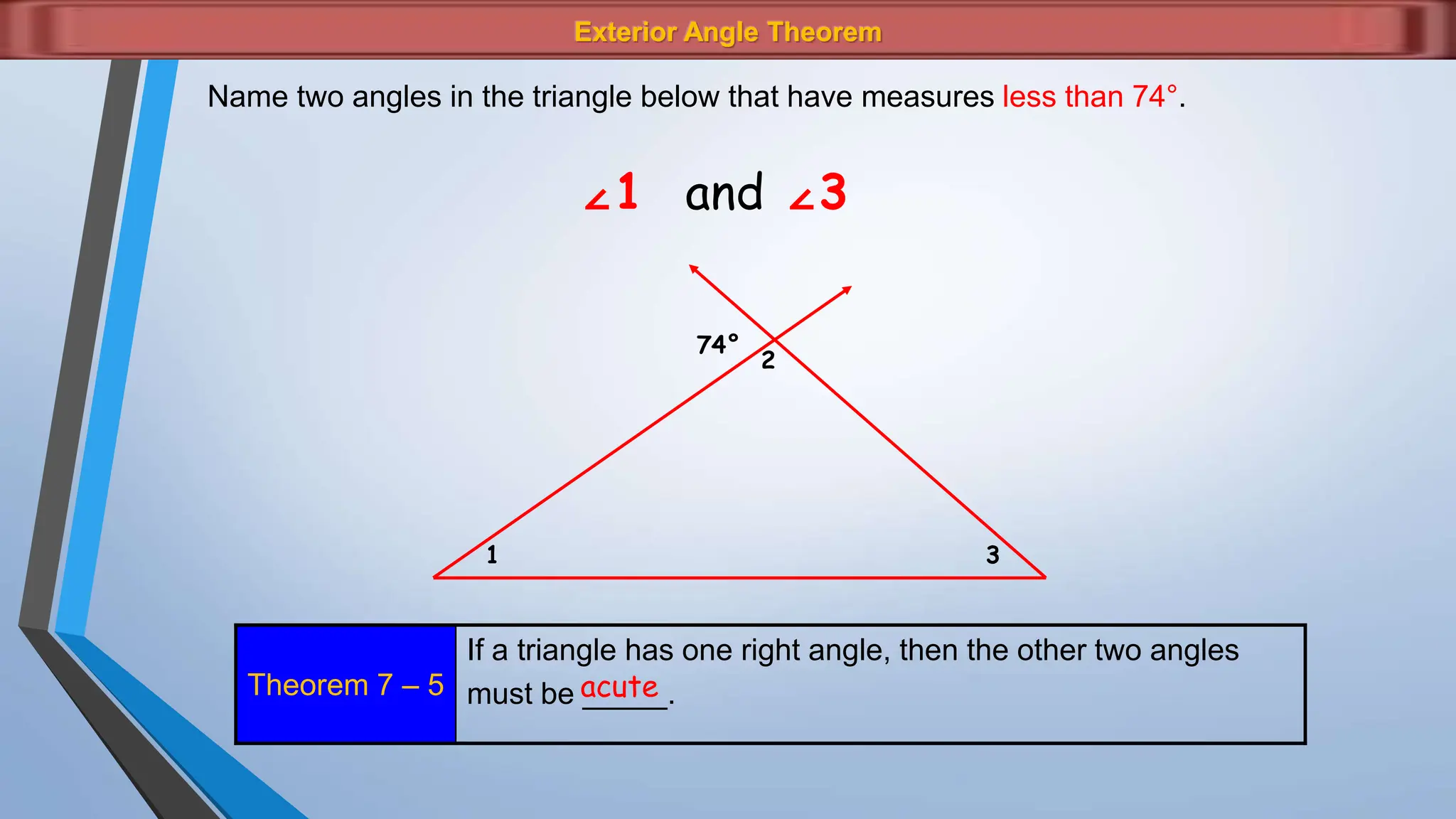
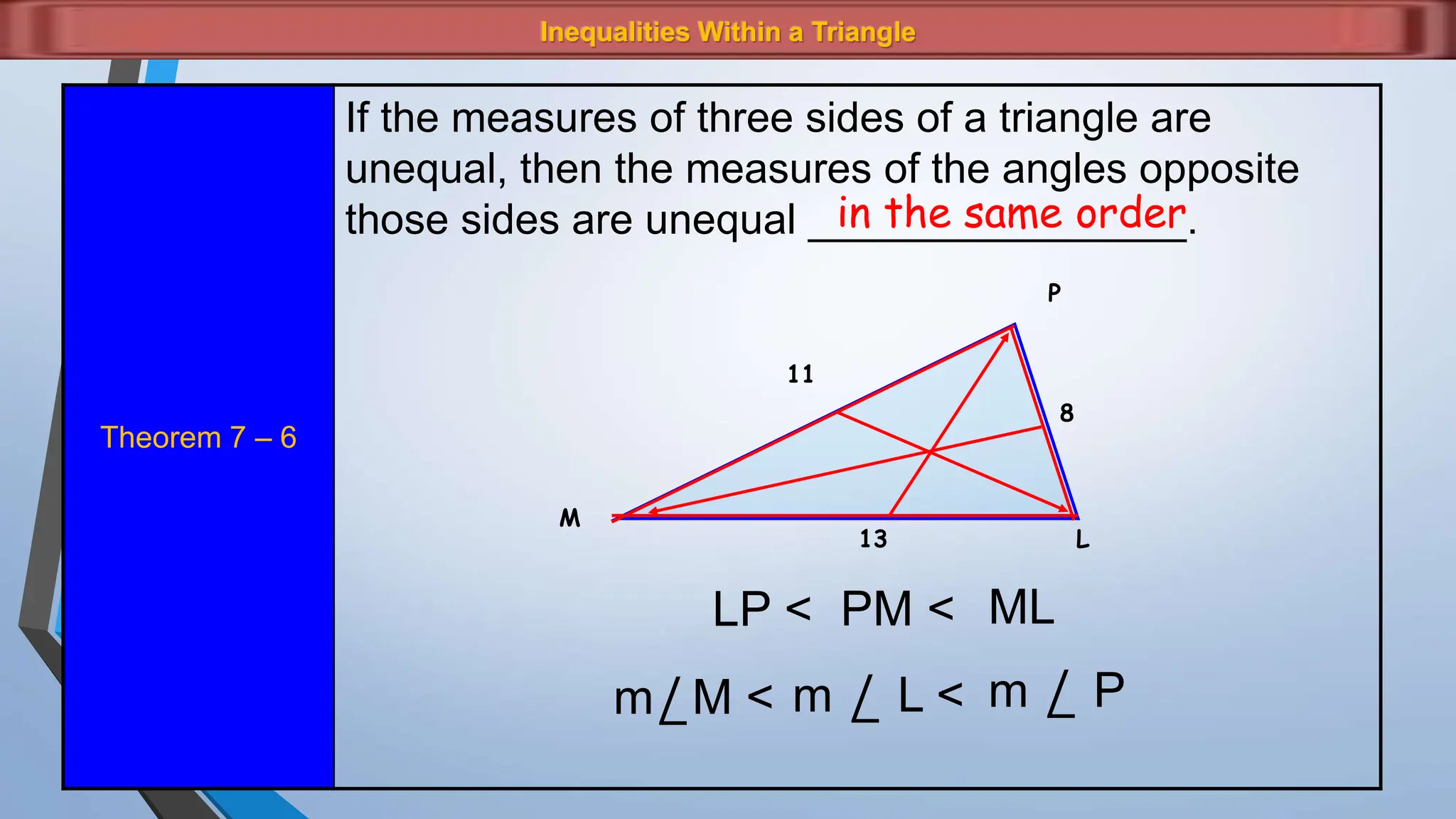
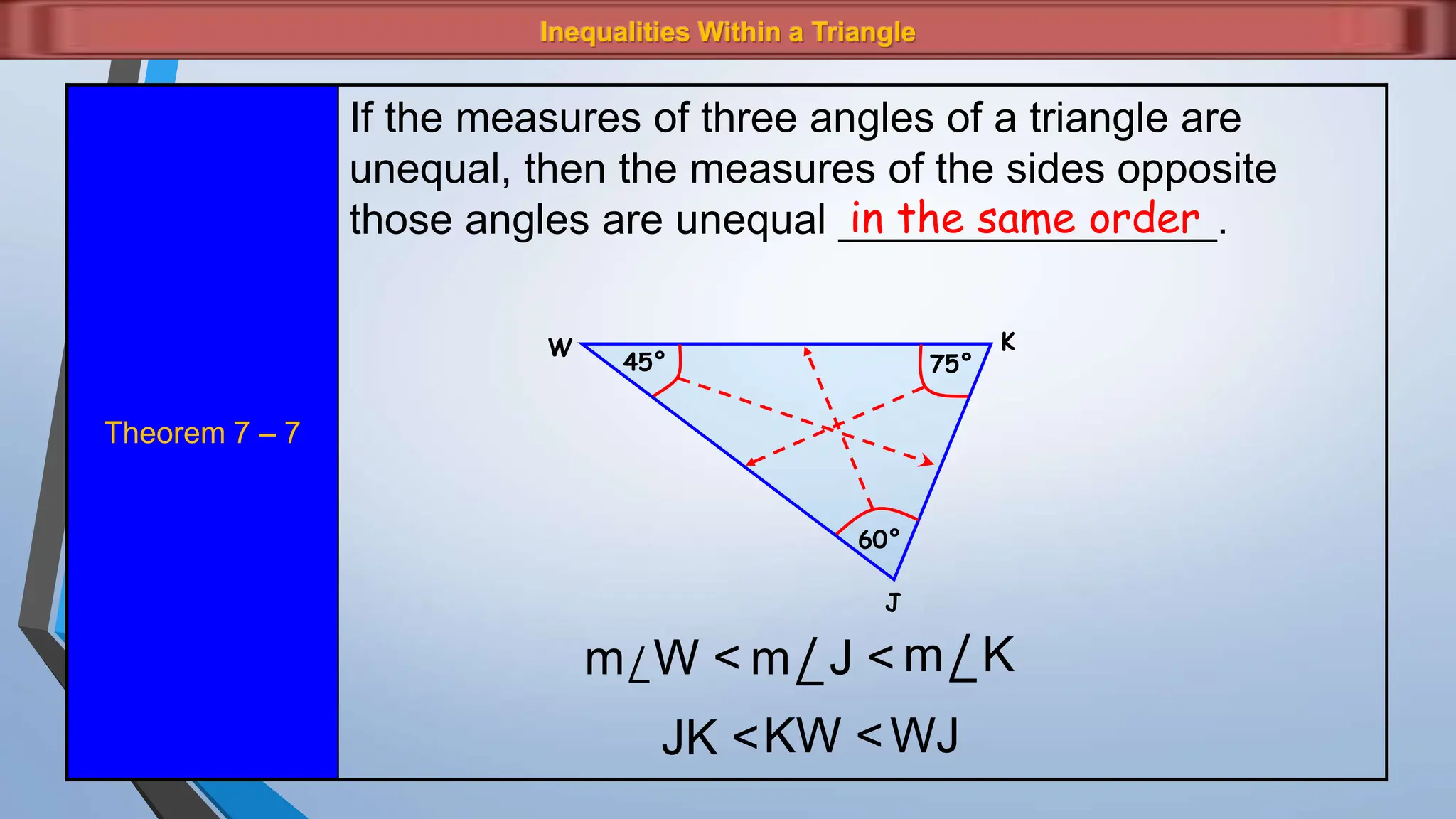
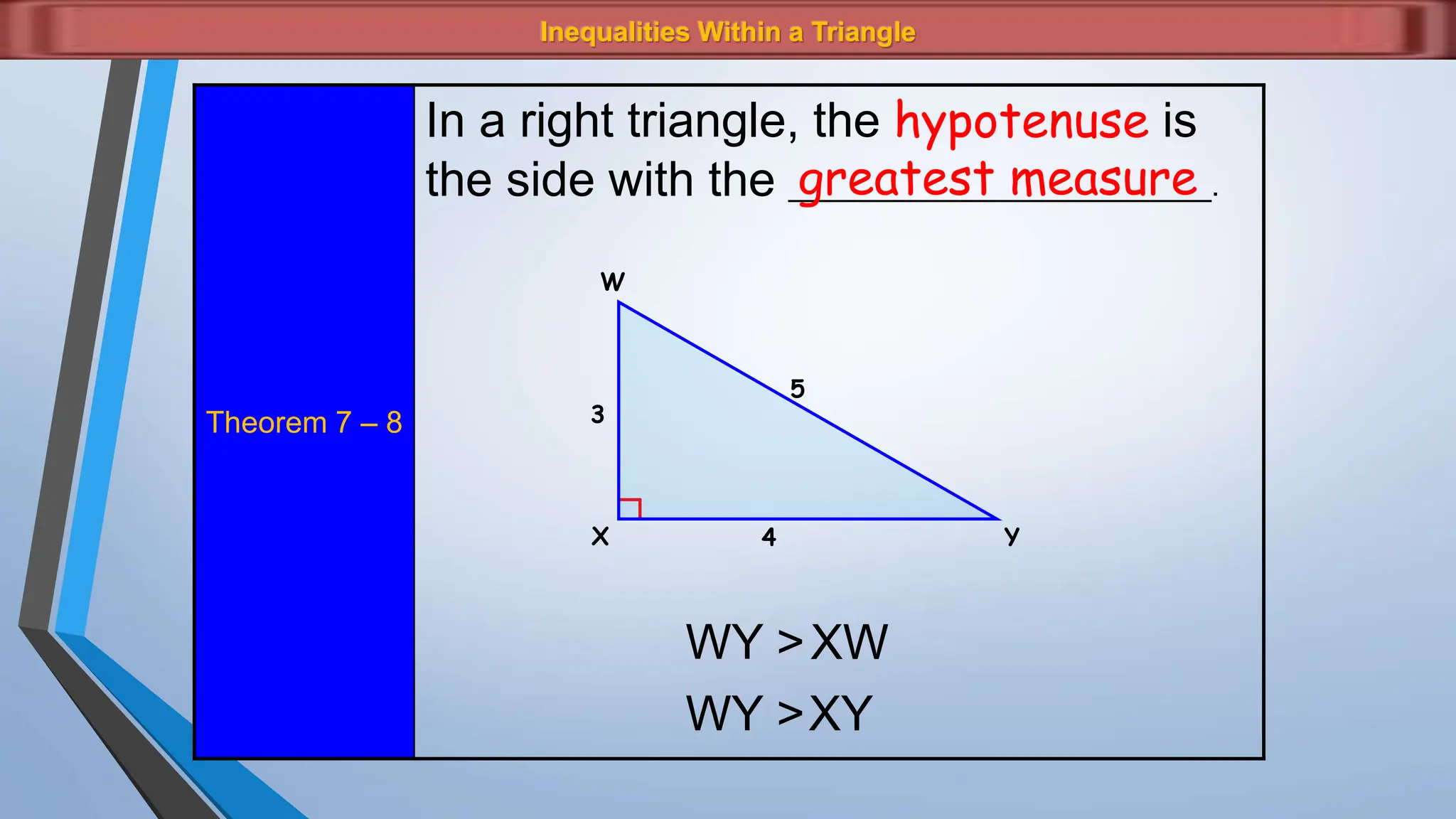
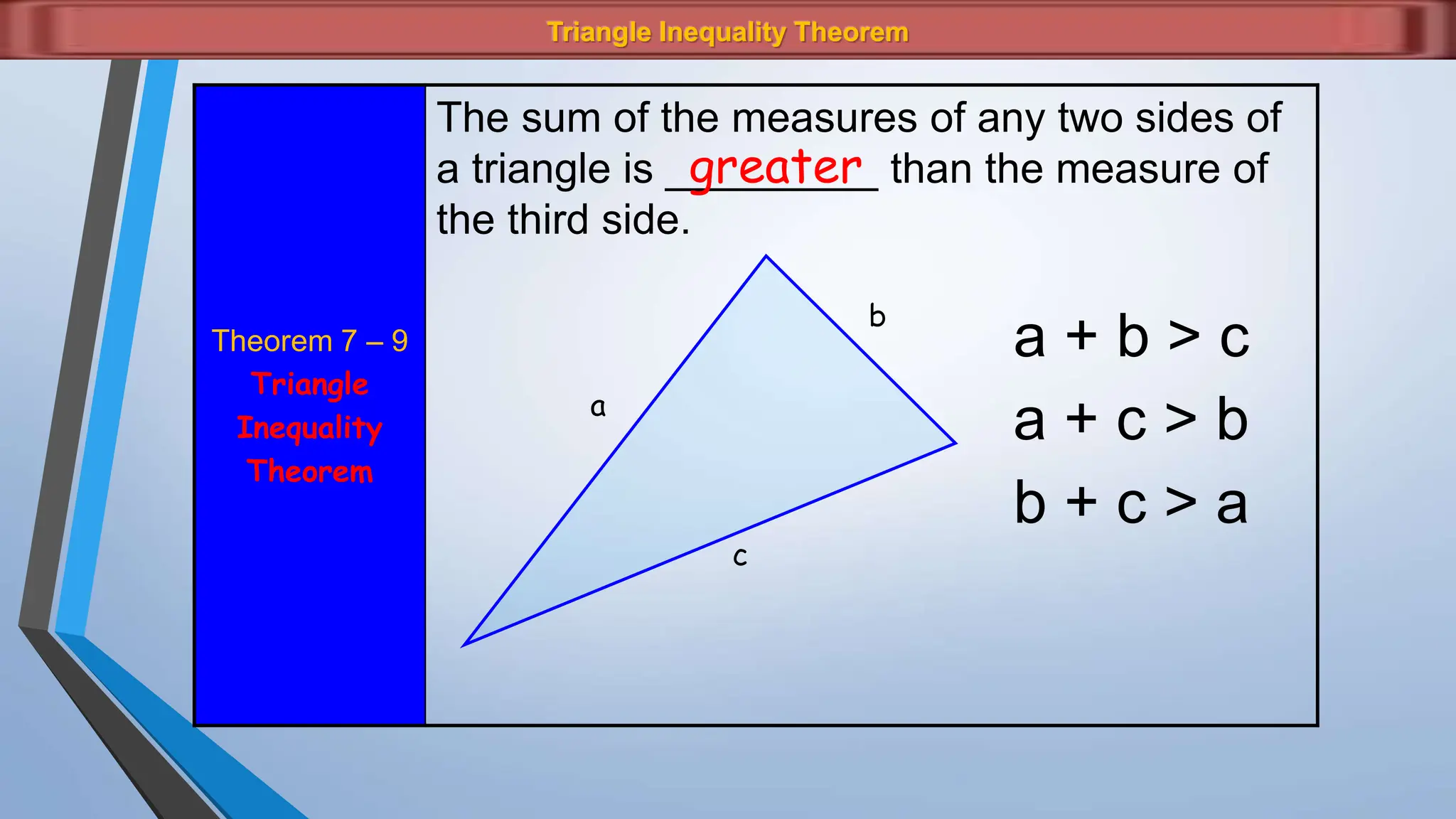
The document discusses various properties and theorems related to angles and segments in triangles, including the triangle inequality theorem, exterior angle theorem, and inequalities within a triangle. Key topics covered include the relationships between angles and sides, as well as methods for establishing the measures of angles and sides based on their properties. Illustrative examples are provided to demonstrate the application of these theorems.

1. Triangle
Inequalitie
s
Balagtas national agricultural high school

2. Segments, Angles, and Inequalities
Property
Transitive
Property
For any numbers a,
b, and c,
1) if a < b and b < c,
then a < c.
2) if a > b and b > c,
then a > c.
if 5 < 8 and 8 < 9,
then 5 < 9.
if 7 > 6 and 6 > 3,
then 7 > 3.

3. Segments, Angles, and Inequalities
Property
Addition and
Subtraction
Properties
Multiplication
and Division
Properties
For any numbers a, b, and c,
For any numbers a, b, and c,
1) if a < b, then a + c < b + c
and a – c < b – c.
2) if a > b, then a + c > b + c
and a – c > b – c.
1 < 3
1 + 5 < 3 + 5
6 < 8
c
b
c
a
and
bc
ac
then
b,
a
and
0
c
If
)




1
c
b
c
a
and
bc
ac
then
b,
a
and
0
c
If
)




2
36
24
2
18
2
12
18
12





9
6
2
18
2
12


18
12

4. Exterior Angle Theorem
You will learn to identify exterior angles and remote
interior angles of a triangle and use the Exterior
Angle Theorem.
1) Interior angle
2) Exterior angle
3) Remote interior angle

5. Exterior Angle Theorem
1
2 3 4
P
Q R
In the triangle below, ∠1, ∠2, and ∠3 are
_______ angles of ΔPQR.
interior
Angle 4 is called an _________ angle
of ΔPQR.
exterior

6. Exterior Angle Theorem
1
2 3 4
P
Q R
An exterior angle of a triangle is an
angle that forms a ____________
with one of the angles of the triangle.
linear pair
In ΔPQR, ∠4 is an exterior angle at R
because it forms a linear pair with ∠3.

7. Exterior Angle Theorem
1
2 3 4
P
Q R
In ΔPQR, ∠1, and ∠2 are the remote
interior angles with respect to ∠4.
____________________ of a triangle
are the two angles that do not form a
linear pair with the exterior angle.
Remote interior angles

8. Exterior Angle Theorem
1
2
3 4 5
In the figure below, ∠2 and ∠3 are remote interior angles with
respect to what angle?∠5

9. Exterior Angle Theorem
Theorem 7 – 3
Exterior Angle
Theorem
The measure of an exterior angle of a triangle
is equal to sum of the measures of its
___________________.
remote interior angles
X
4
3
2
1
Z
Y
m∠4 = m∠1 + m∠2

12. Exterior Angle Theorem

13. Exterior Angle Theorem
Theorem 7 – 4
Exterior Angle
Inequality
Theorem
The measure of an exterior angle of a triangle
is greater than the measures of either of its
two ____________________________.
remote interior angles
X
4
3
2
1
Z
Y
m∠4 > m∠1
m∠4 > m∠2

14. Exterior Angle Theorem
∠1 and ∠3
74°
1 3
2
Name two angles in the triangle below that have measures less than 74°.
Theorem 7 – 5
If a triangle has one right angle, then the other two angles
must be _____.
acute

15. Exterior Angle Theorem
3
and
1 


16. Exterior Angle Theorem
The feather–shaped leaf is called a pinnatifid.
In the figure, does x = y? Explain.
x = y
?
__ + 81 = 32 + 78
28
28°
109 = 110
No! x does not equal y

17. Inequalities Within a Triangle
Theorem 7 – 6
If the measures of three sides of a triangle are
unequal, then the measures of the angles opposite
those sides are unequal ________________.
13
8
11
L
P
M
in the same order
LP < PM < ML
m⎳M < m ⎳ P
m ⎳ L <

18. Inequalities Within a Triangle
Theorem 7 – 7
If the measures of three angles of a triangle are
unequal, then the measures of the sides opposite
those angles are unequal ________________.
in the same order
JK <KW <WJ
m⎳W < m⎳K
m⎳J <
J
45°
W K
60°
75°

19. Inequalities Within a Triangle
Theorem 7 – 8
In a right triangle, the hypotenuse is
the side with the _________________________.
greatest measure
WY >XW
3
5
4 Y
W
X
WY >XY

20. Inequalities Within a Triangle
A

BC
The longest side is
So, the largest angle is
L

The largest angle is
MN
So, the longest side is

21. Triangle Inequality Theorem
Theorem 7 – 9
Triangle
Inequality
Theorem
The sum of the measures of any two sides of
a triangle is _________ than the measure of
the third side.
greater
a
b
c
a + b > c
a + c > b
b + c > a

22. Triangle Inequality Theorem
Can 16, 10, and 5 be the measures of the
sides of a triangle? No!
16 + 10 > 5
16 + 5 > 10
However, 10 + 5 > 16