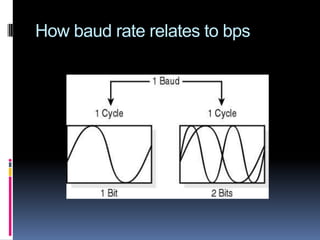
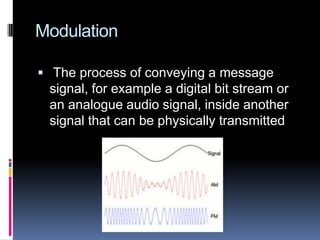
This document discusses key concepts related to digital transmission including: - Bits per second and baud rate which measure transmission speed and signal changes. - Modulation techniques like QAM that represent data using signal amplitude and phase. - Error checking methods like parity bits, checksums, and CRC that detect errors in transmission. - Factors that affect transmission times like bandwidth, distance, and error checking overhead.

1. TRANSMISSION

2. Bits per second (bps) aka bit rate
 A measure of transmission speed. The
number of binary digits (0 or 1) which can
be transmitted per second
 Not to be mistaken for Bytes per second
(Bps)
 When converting Bps to bps, remember
that there are 8 bits to a Byte
 Therefore 10MB = 10 x 8 Mb = 80Mb

3. Baud Rate aka symbol rate
 A measure of how fast a change of state
occurs (i.e. a change from 0 to 1)
 The number of signal events occurring
each second along a communication
channel
 Because a signal can contain more than
one bit of data, the baud rate and the bit
rate may be different. E.g. 1200 baud
might transmit at 4800 bps.

4. Baud Rate aka symbol rate
 The number of different symbols required
depends on the number of bits used in a
single signal event
 E.g. if there are 4 bits represented in each
baud, there will need to be 16 different
symbols.

5. Baud Rate aka symbol rate
E.g. 24 = 16
0000 0001 0010 0011
0100 0101 0110 0111
1000 1001 1010 1011
1100 1101 1110 1111
E.g. 22 = 4
00 01 10 11

6. How baud rate relates to bps

7. Example
An analogue signal carries 6 bits in each
signal event. If 1000 signal events are sent
per second, what is the baud rate and bit
rate?
Solution:
 Baud rate = 1000 bauds per second
 Bit rate = 1000 x 6 = 6000bps

8. Modulation
 The process of conveying a message
signal, for example a digital bit stream or
an analogue audio signal, inside another
signal that can be physically transmitted

9. QAM
 Most current connections to the Internet
use Quadrature Amplitude Modulation
(QAM).
 This system represents different bit
patterns by altering the amplitude and
phase of the wave.
 16QAM uses 16 different symbols to
represent 4 bits/symbol, 32QAM uses 32
different symbols to represent 5
bits/symbol, etc.

10. Group Task Activity
Calculate the minimum transmission time
required to transfer a 1kB packet at 10Mbps
to a satellite located 40 000km above Earth.
 3 x 108 m/s = 300 000 000 m/s
 Time for the first part of the signal to reach
the satellite will be
40 000 000 ÷ 300 000 000 = 0.1333
seconds

11. Group Task Activity
 Now we need to calculate the time taken
from when the first part of the signal is
placed on the medium until the last signal
is placed on the medium.
 10Mb (megabits) of data are placed on the
medium in 1 second. We are placing a
1kB (kilobyte) packet on the medium.
 10Mb = ~ 10 000kb
 1 kB = 8kb
∴ 8kb will take 8 ÷ 10 000 = 0.0008 seconds
for the sender to place on the medium.

12. Group Task Activity
 So the first part of the signal will arrive at
the satellite in 0.1333 seconds; the
remainder of the signal follows during the
next 0.0008 seconds.
 Therefore, the minimum time taken until
the entire message reaches the satellite is
0.1333 + 0.0008 = 0.1341 seconds

13. Group Task Discussion
Why is the speed of wave propagation
particularly significant over longer distances
when each data packet must be
acknowledged before the next one can be
sent? Discuss

14. Group Task Activity
 The time taken for the signal to physically
propagate through the medium (signal
latency) adds to the time between a
packet being received by the destination
and acknowledgements being received by
the sender. Furthermore the propagation
time must be added to the time taken for
every packet to reach it’s destination.

15. Group Task Activity
As CPU speeds increase and motherboards
transfer data faster, will the speed of wave
propagation within and between
motherboard components become
significant? Discuss
 Distances between motherboard
components are miniscule compared to
distances on a global scale.

16. Group Task Activity
 Consider a distance of 300mm between
motherboard components.
At 2 x 108 m/s the propagation time is just
0.3 ÷ 200 000 000 = 0.0000000015
seconds.
∴ CPU speeds would need to increase
enormously before propagation speeds will
become a significant motherboard issue.

17. Bandwidth
 Not to be confused with speed or bps
 The range of frequencies used by a
transmission channel (the difference
between the highest and lowest)
 Expressed in hertz (Hz)
 E.g. Standard telephone equipment used
for voice operates within a frequency
range from about 200Hz to 3400Hz, so
the available bandwidth is 3200Hz
(3.2KHz).

18. Example
A fibre-optic cable has a high bandwidth.
When cable television is transmitted through
fibre-optic cable, many different channels
can be transmitted at the same time.

19. Group Task Activity
Calculate the time taken to transfer a 2MB file
over each of the below communication
methods.
 First we need to convert all numbers to bits
 2MB = 2 000 000 Bytes
 2 000 000 Bytes = 16 000 000 bits
1. 56kbps = 56 000bps. Time = 16 000 000 ÷
56 000
= 286 seconds

20. Group Task Activity
2. 10 Mbps
16 000 000 ÷ 10 000 000 = 1.6 seconds
3. 100Mbps
16 000 000 ÷ 100 000 000 = 0.16 seconds
4. 1000Mbps
16 000 000 ÷ 1 000 000 000 = 0.016
seconds

21. Group Task Activity
5. 1.5Mbps
16 000 000 ÷ 1 500 000 = 10.7 seconds
6. 64QAM uses 64 symbols to represent 6
bits/symbol. Therefore 4Msym/s is
equivalent to
4 x 6 = 24Mbps = 24 000 000bps
16 000 000 ÷ 24 000 000 = 0.67 seconds

22. Group Task Activity
Identify and discuss reasons why it is unlikely
that the minimum times calculated above would
be realised in reality.
 Errors including the time taken to resend
faulty packets.
 Other simultaneous transmissions occurring.
 Protocol headers/trailers and time waiting for
acknowledgements
 Time to pass through other components such
as NICs, routers, etc.

23. Error Checking Methods
When an error is detected the receiver can
respond in various ways depending on the
rules of the particular protocol.
 Parity bit check
 Check sum
 Cycle redundancy check (CRC)

24. Parity bit check
 The simplest form of error detection involves
adding a parity bit to the data bits
 The sender computes an additional bit based
on the given data bits
 The receiver performs the same computation
and verifies that the parity bits agree
 The computation is chosen so that a one-bit
alteration can be detected
 Parity can be even or odd, this is established
during handshaking
 E.g. For even parity, the sender sets the
parity bit so that the total number of 1 bits is
even

25. Parity bit check

26. Checksums
 All the 1s and 0s in a block of data are
summed to make a total and the receiver
calculates a checksum value. If the sent
value does not agree, then an error is
detected. If the count matches, it is
assumed that a complete transmission
was received.
 The position of the error is unknown

27. Group Task Discussion Activity
IP datagrams include a 16-bit checksum
calculated using just their header whilst TCP
segments include a 16-bit checksum
calculated using the entire message.
Discuss possible reasons for this difference
and describe likely differences between the
accuracy of IP and TCP checksums.

28. Group Task Discussion Activity
 IP aims to route messages and isn’t
concerned with guaranteeing delivery. The
header contains all the data needed for
routing
 TCP acknowledges each segment,
therefore it checks the accuracy of the
entire segment
 IP checksums are calculated over a
smaller number of bytes compare to TCP
checksums, this tend to be more accurate.

29. Cyclic Redundancy Check (CRC)
 The most accurate error check
 Calculated using division rather than addition
 The data is divided into predetermined
lengths and divided by a fixed number. The
remainder of the calculation is attached and
sent with the data.
 When the data is received, the remainder is
recalculated. If the remainders do not match,
an error in transmission has occurred.
 There are a number of different standards for
CRC. A 32-bit CRC achieves a 99.99%
detection of all possible errors.