Download to read offline
Uploaded byUniversity of Ulsan
Training Models Chapter 4 Hands on Machine Learning Book
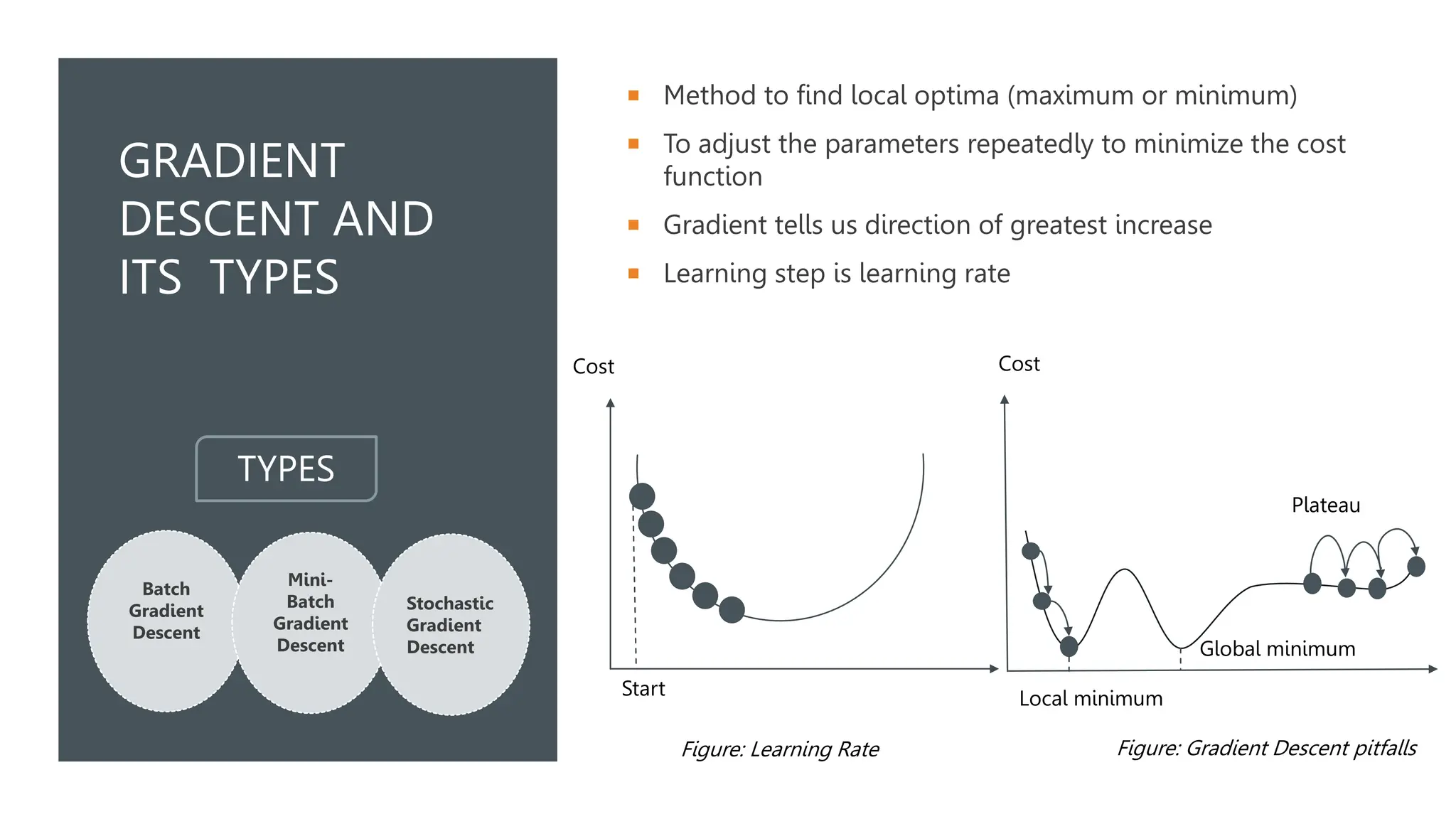
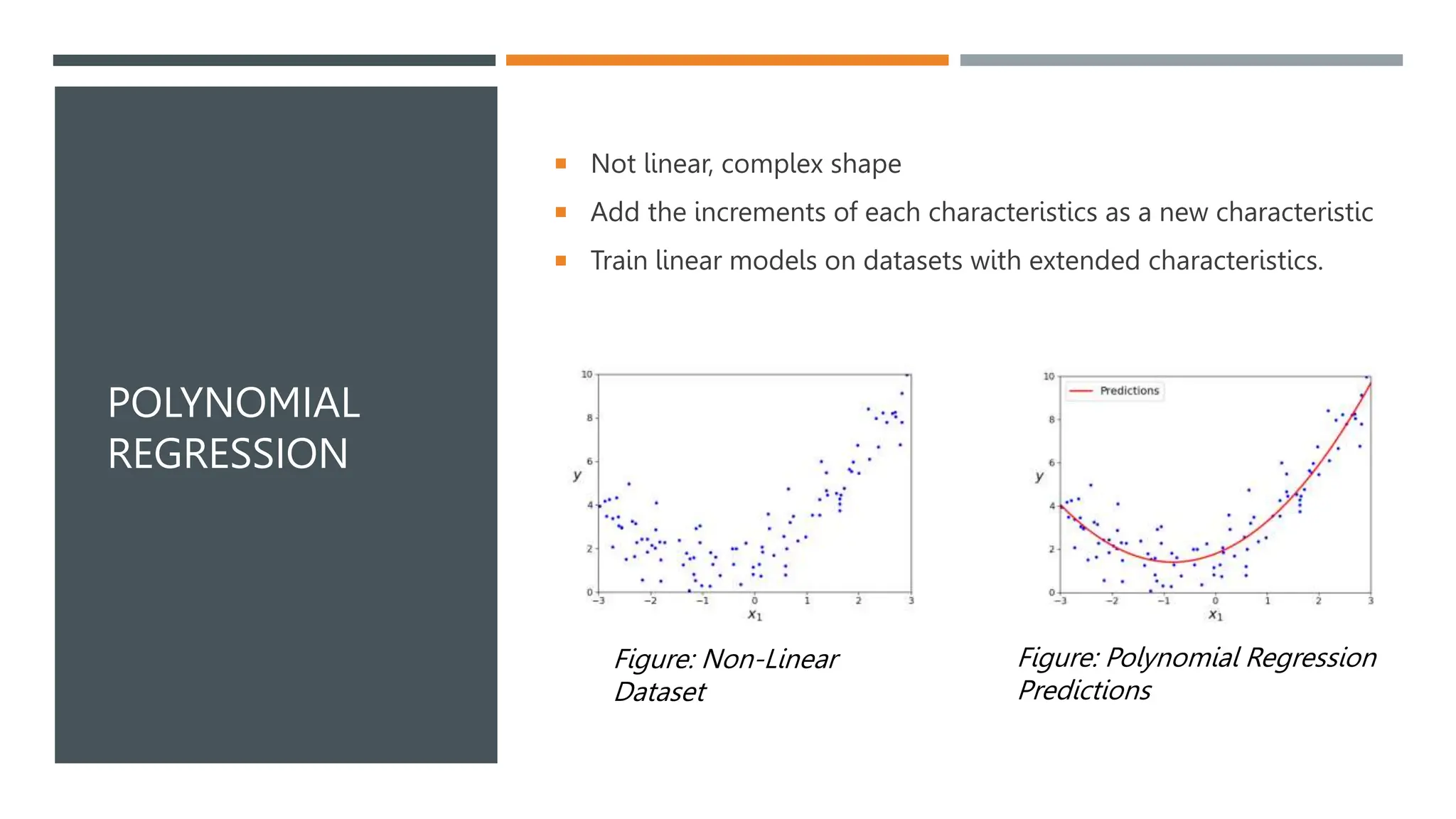
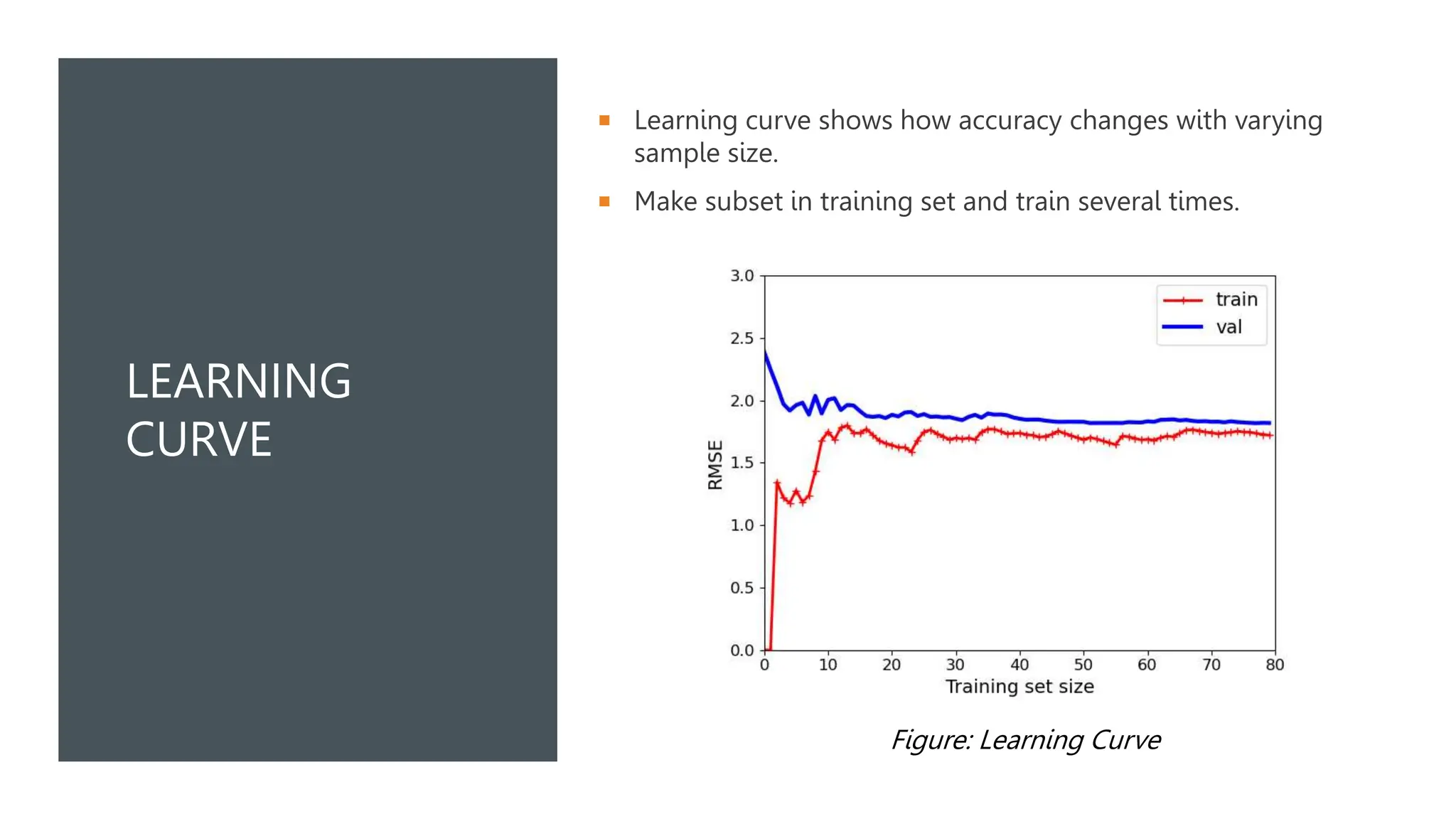
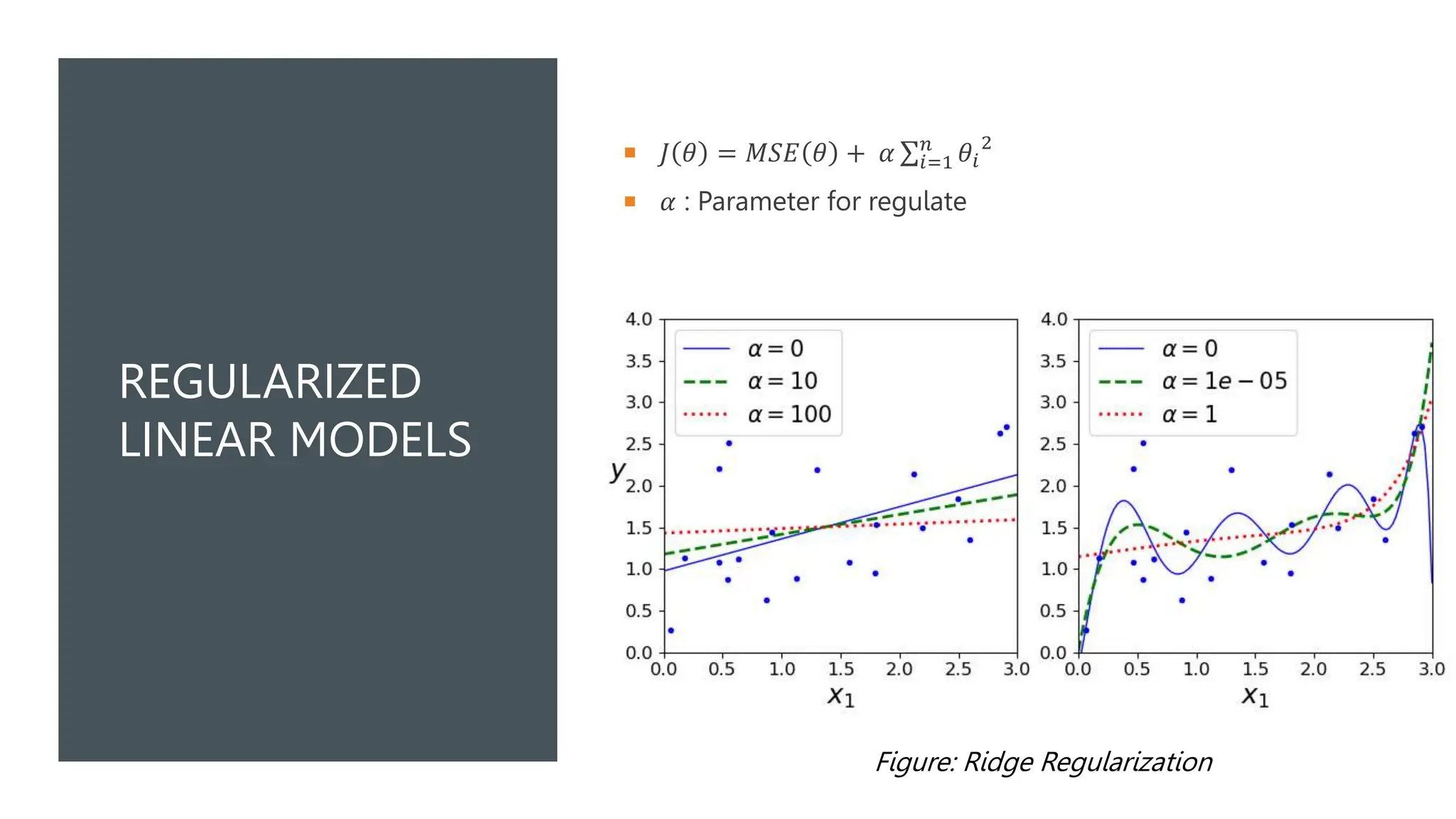
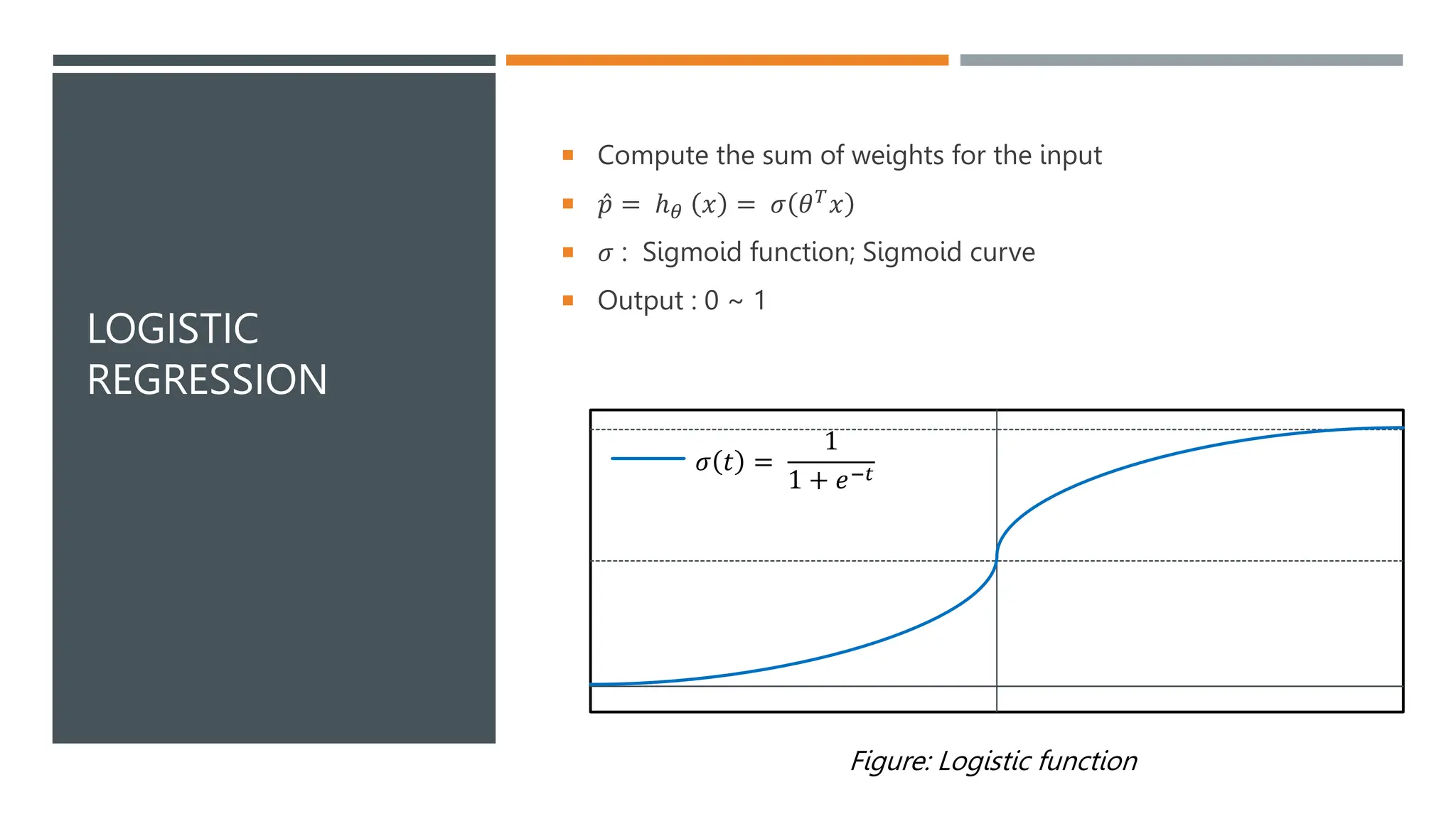
The document covers various machine learning topics including linear and polynomial regression, gradient descent, and logistic regression. It explains key concepts such as mean squared error, cost functions, and learning curves, as well as types of gradient descent methods. Regularization techniques for improving model performance are also discussed, along with the application of sigmoid functions in logistic regression.
Training Models Chapter 4 Hands on Machine Learning Book
- 1.
- 2. CONTENTS Linear Regression Gradient Descent Polynomial Regression Learning Curve Regularized Linear Models Logistic Regression
- 3. LINEAR REGRESSION 𝑦 =𝜃0 + 𝜃1𝑥1 + 𝜃2𝑥2 + 𝜃3𝑥3 + ⋯ + 𝜃𝑛𝑥𝑛 • y ∶ predicted value • n : size of data • x : input data 𝑀𝑆𝐸 𝑋, ℎ𝜃 = 1 𝑚 𝑖=1 𝑚 (𝜃𝑇𝑥 𝑖 − 𝑦 𝑖 )2 • Mean Squared Error Cost function Predicted Value – Actual Value Similar to the actual values, MSE value is small
- 4. GRADIENT DESCENT AND ITS TYPES Method to find local optima (maximum or minimum) To adjust the parameters repeatedly to minimize the cost function Gradient tells us direction of greatest increase Learning step is learning rate Cost Local minimum Global minimum Plateau Figure: Gradient Descent pitfalls Cost Start Figure: Learning Rate Batch Gradient Descent Mini- Batch Gradient Descent Stochastic Gradient Descent TYPES
- 5. POLYNOMIAL REGRESSION Figure: Non-Linear Dataset Figure: PolynomialRegression Predictions Not linear, complex shape Add the increments of each characteristics as a new characteristic Train linear models on datasets with extended characteristics.
- 6. LEARNING CURVE Learning curveshows how accuracy changes with varying sample size. Make subset in training set and train several times. Figure: Learning Curve
- 7. REGULARIZED LINEAR MODELS 𝐽𝜃 = 𝑀𝑆𝐸 𝜃 + 𝛼 𝑖=1 𝑛 𝜃𝑖 2 𝛼 : Parameter for regulate Figure: Ridge Regularization
- 8. LOGISTIC REGRESSION Compute thesum of weights for the input 𝑝 = ℎ𝜃 𝑥 = 𝜎 𝜃𝑇𝑥 𝜎 : Sigmoid function; Sigmoid curve Output : 0 ~ 1 Figure: Logistic function 𝜎 𝑡 = 1 1 + 𝑒−𝑡
- 9.
Editor's Notes
- #8 Consider talking about: Cybernetics and brain simulation Symbolic Sub-symbolic Statistical learning Integrating the approaches
- #9 Consider talking about: Search and optimization Logic Probabilistic methods for uncertain reasoning Classifiers and statistical learning methods Artificial neural networks Evaluating progress