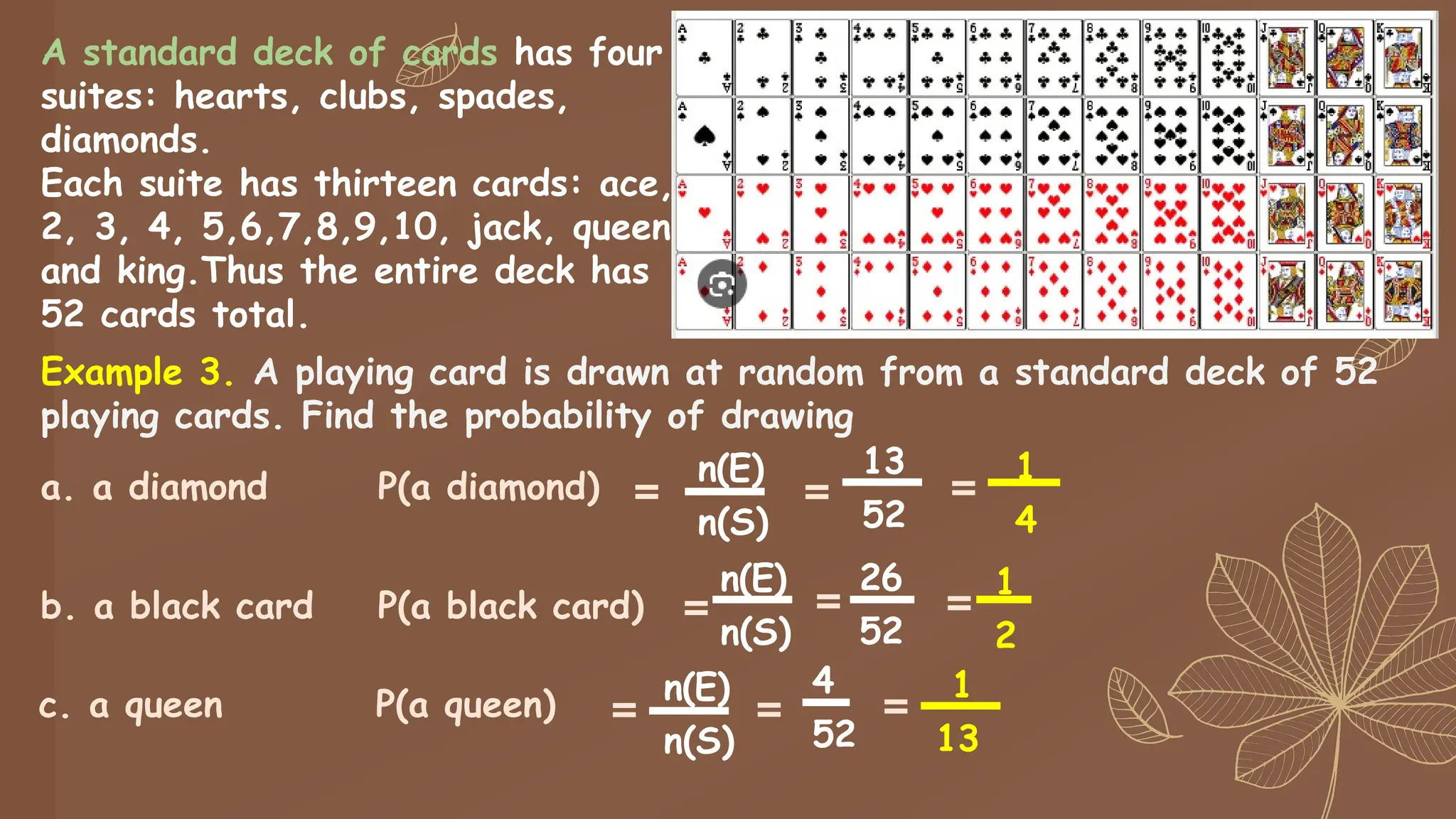
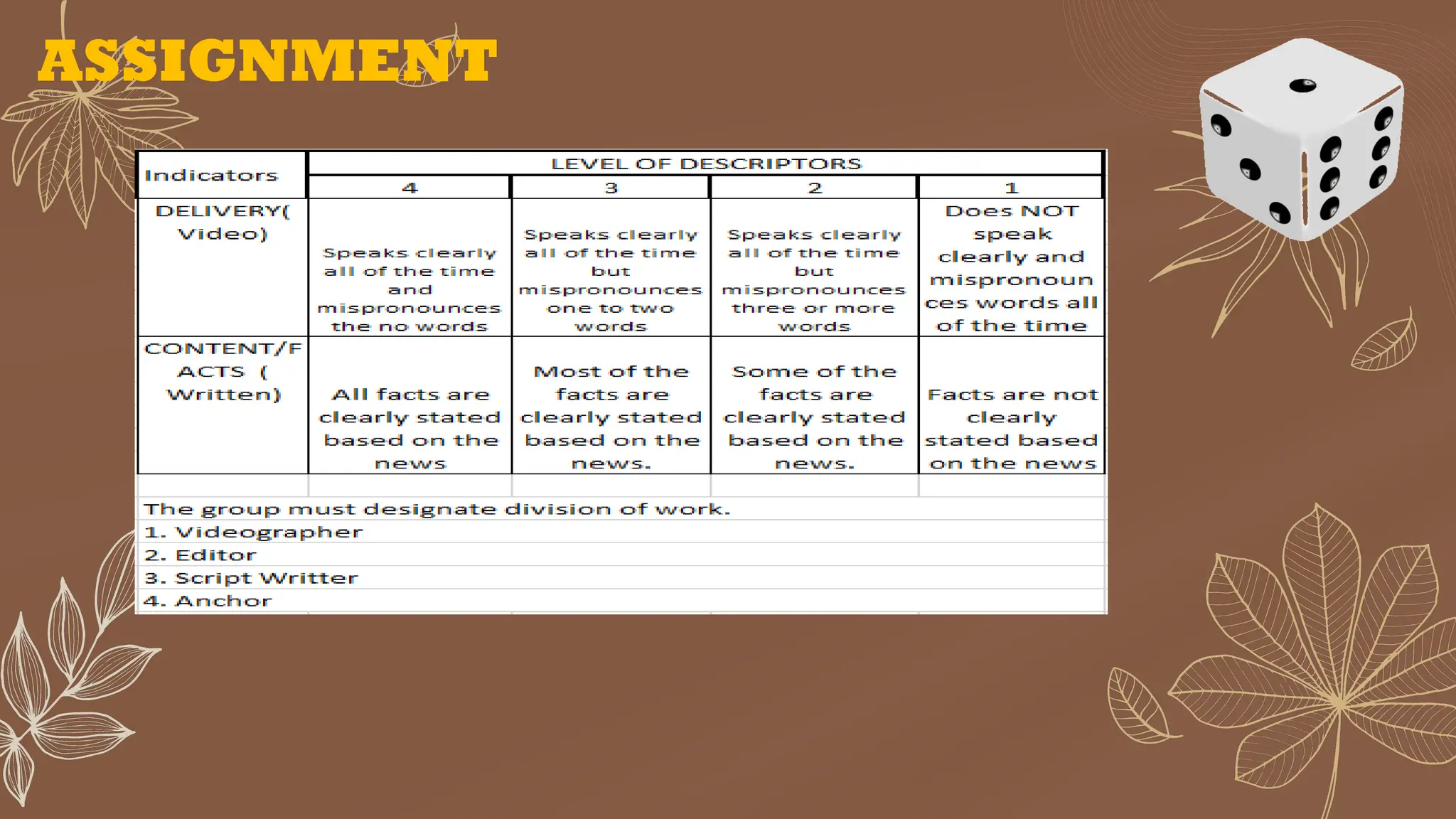
The document provides a comprehensive overview of probability and simple events, detailing methods for defining, calculating, and applying probability to real-world scenarios. It includes interactive gameplay examples like rolling colored dice and coin flips, where participants record outcomes and compare experimental probabilities to theoretical probabilities. Additionally, it covers the properties of probability, sample spaces, and practical applications in various fields, such as genetics and weather forecasting.

1. Probability of
Simple Events

2. Objectives:
1. Define probability and simple events.
2. Understand the concept of probability
through practical examples.
3. Calculate the probability of simple
events.
4. Apply the concept of probability to
solve real-world problems.

3. Gameplay:
1.Each player takes turns rolling the colored dice.
2.After each roll, they identify the color that appears and record
it.
3.Players can pick their color events, such as "rolling a primary
color( red, blue,yellow)" "rolling a secondary
color( orange,purple,green)" or "rolling a warm color (red, orange,
or yellow).“
4.The player with the most accurate predictions or highest
probability of desired events wins!
"Colorful Cube Challenge"

4. "Colorful Cube Challenge”
Instructions: Identify the following in the previous
activity.
1.Experiment:
2.Outcomes:
3.Sample Space:
4.Event:

5. "Colorful Cube Challenge"
Instructions:
1.Experiment: The experiment is rolling the colored dice. Each roll represents one
trial of the experiment.
2.Outcomes: The outcomes are the different colors that appear on the face of
the dice after each roll. So, the outcomes could be red, blue, green, yellow,
orange, or purple.
3.Sample Space: The sample space is the set of all possible outcomes of the
experiment. In this game, the sample space would be {red, blue, green, yellow,
orange, purple}. Give example on how to determine the number of sample space like
tossing of coins.
4.Event: An event is a subset of the sample space, or in simpler terms, it's
something that can happen. For example, "rolling a primary color (red, blue, or
green)" would be an event.

6. Toss Quest!
Steps:
1.Ask someone to volunteer to be the first to flip the coin.
2.Before they flip the coin, ask the audience to predict the outcome
(heads or tails) and write down their predictions.
3.Have the volunteer flip the coin and observe the result.
4.Record the outcome (heads or tails), in table form.
5.Repeat steps 3-4 several times, with different volunteers if possible.
6.After several flips, tally up the number of times heads and tails
appeared.
7.Calculate the experimental probability of getting heads or tails by
dividing the number of times each outcome occurred by the total number
of flips.
8.Compare the experimental probabilities to the theoretical probability
(1/2 for each outcome) and discuss any discrepancies.

7. Let's walk through each step with clear examples:
1. Have the volunteer flip the coin and observe the result.
Volunteer flips the coin.
Result: Heads.
2-3. Record the outcome (heads or tails), in table form until
five(5) flip

8. 4. After several flips, tally up the number of times heads
and tails appeared.
Number of Heads: 2
Number of Tails: 1
5. Calculate the experimental probability of getting heads or
tails by dividing the number of times each outcome occurred
by the total number of flips.
a. Experimental Probability of Heads = Number of Heads /
Total Flips = 2 / 3 ≈ 0.67
b. Experimental Probability of Tails = Number of Tails /
Total Flips = 1 / 3 ≈ 0.33
6.Theoretical Probability of Heads = 1/2 = 0.5
Theoretical Probability of Tails = 1/2 = 0.5

9. Toss Quest!
Steps:
1.Ask someone to volunteer to be the first to flip the coin.
2.Before they flip the coin, ask the audience to predict the outcome
(heads or tails) and write down their predictions.
3.Have the volunteer flip the coin and observe the result.
4.Record the outcome (heads or tails), in table form.
5.Repeat steps 3-4 several times, with different volunteers if possible.
6.After several flips, tally up the number of times heads and tails
appeared.
7.Calculate the experimental probability of getting heads or tails by
dividing the number of times each outcome occurred by the total number
of flips.
8.Compare the experimental probabilities to the theoretical probability
(1/2 for each outcome) and discuss any discrepancies.

10. Guide Questions:
What do you think this activity implies and
how it relates to making predictions?
Through this activity, you can see how probability works in a
simple and engaging way. It allows you to make predictions,
observe outcomes, and understand the relationship between
the number of favorable outcomes and the total number of
possible outcomes.

11. PROBABILITY
PROBABILITY
- A measure of how often a particular
event will happen.
-The chance that something will
happen.
CHANCE POSSIBILITY EXPECTED
-often represented as a fraction,
decimal, or percentage.

12. PROBABILITY LINE
0% 25% 50% 75%
100%
0
Impossible
¼ or .25
Not Very
Likely
½ 0r .5
Equally Likely
¾ or .75
Somewhat
Likely
1
Certain
Properties of Probability of an Event
1.A probability is a number between 0 and 1, inclusive.
2. The probability of an event that cannot be happen is 0.
3. The probability of an event that must happen is 1.

13. Definition:
1)The probability of simple event is
finding the probability of a single
event occurring.
- refers to the likelihood or chance that
a specific outcome will occur in an
experiment or situation where there are
only one possible outcome

14. 2) The notation P(E) is read as “the
probability of an event E” or simply the
probability of E”.
P(E) =
n ( E)
n ( S)
n(event)- number of favorable outcomes of the event.
n(sample Space)- total number of possible outcomes.
P(Event) =
No. of favorable outcome of an event
Total no. of possible outcome
in symbols,

15. Example 1: Flip a coin - Tossing a Coin What is the probability
of flipping a head?
When a coin is tossed, there are two possible outcomes: head (H) or tail(T)
n (head)
n(sample space)
P(head ) =
P(head) = 1 = 1
2
2
Sample Space = (H, T)
n(S)= 2
Event = (H)
n(E) = 1
The probability is 1 out of 2 or 0.5 or
50% the probability of flipping a HEAD
is ½.

16. Example 2: Roll a dice - Throwing Dice
What is the probability of rolling a prime number on
a number cube?
n(E)
n(S)
1
2
P(prime numbers) =
3
6
=
=
Sample Space = {1,2,3,4,5,6}
n(S)=6
Event = {2,3,5}
n(3)=3

17. A standard deck of cards has four suites: hearts, clubs, spades, diamonds.
Each suite has thirteen cards: ace, 2, 3, 4, 5,6,7,8,9,10, jack, queen and
king.Thus the entire deck has 52 cards total.

18. A standard deck of cards has four
suites: hearts, clubs, spades,
diamonds.
Each suite has thirteen cards: ace,
2, 3, 4, 5,6,7,8,9,10, jack, queen
and king.Thus the entire deck has
52 cards total.
Example 3. A playing card is drawn at random from a standard deck of 52
playing cards. Find the probability of drawing
a. a diamond
P(a black card)
c. a queen
P(a diamond)
b. a black card
P(a queen)
=
=
=
n(E)
n(S)
n(E)
n(S)
n(E)
n(S)
=
=
=
13
52
26
52
4
52
=
=
=
1
4
1
2
1
13

19. Roll and I Compete!
Each group will have 6 representatives to compete,
number(1-6). Each group will be given 3 minutes to talk
about how they will answer the problem. Determine the
sample space and the event in each number. Then
each member will compete depends upon the number
appeared in rolling a die. Each group will be given one
minute to answer each item.

20. Questions: Three coins are tossed. What is the probability of
getting the following. Express your answer in fraction form.
a. three heads?
b. two heads?
c. one head?
d. at least two tails?
e. at most two tails?
f. no tail?
greater than or equal
less than or equal
Roll and I Compete!
S = {HHH, HHT, HTH,
HTT, TTT, THH, THT,
TTH}
n(s)= 8

21. Questions: Three coins are tossed. What is the probability of getting:
a. three heads?
b. two heads?
c. one head?
d. at least two tails?
e. at most two tails?
f. no tail?
greater than or equal
less than or equal
S = {HHH, HHT, HTH, HTT,
TTT, THH, THT, TTH}
n(s)= 8
1
8
3
8
3
8
4
8
7
8
1
8
1
2
=
Key Answer!

22. SCIENCE- WEATHER- when planning an outdoor activity, people
generally check the probability of rain. Meteorologist also predict
the weather, typhoon or natural resources.
Application of probability in daily life and other field of Education

23. Genetics Offspring
In genetics, theoretical probability can be used to calculate the
likelihood that offspring will be a certain sex, or that offspring
will inherit a certain trait or disease if all outcomes are equally
possible. It can be used to calculate probabilities of traits
T t
T TT Tt
t Tt tt
MENDEL’S LAW OF DOMINANCE AND RECESSIVENESS
(Punnett Square)
Dominant Trait (T)
Recessive Trait (t)
Tall – TT (dominant)
Short- tt( recessive)
Genotype: ¼ or 25% homozygous tall
½ or 50% heterozygous tall
¼ or 25% homozygous short
Phenotype: ¾ or 75% Tall
¼ or 25 % short

24. Students will reflect on the following pictures by answering the
given questions below.
1.How do you define probability of simple event?
2.How do you determine the probability of simple event?
3.How can you relate the given set of pictures in probability?
Explain your answer.
4. Is probability be a deciding factor in choosing and selecting
your preference? Justify your answer.
Courses offered University Passing Rate

25. 1. P(sum is 7) =
In the experiment of rolling two six-sided dice, find the
following:
2. P(sum is 10) =
Quiz: Answer the following questions involving probability of
simple event. Express your answer in lowest term.
Find the probability that
3. at least one die shows a 4.
4. both dice show the same number.
a. P(at least one die shows 4) =
b. P(both dice show the same number)

26. 1. P(sum is 7) = n(sum is 7)
n(sample space)
In the experiment of rolling two six-sided dice, find the
following:
6
36
= {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
1
6
=
2. P(sum is 10) =
n(sum is 10)
n(sample space)
3
36
= {(4, 6), (5, 5), (6, 4)}
1
12
=
Quiz: Answer the following questions involving probability of simple event.
Express your answer in lowest term.

27. Find the probability that
3. at least one die shows a 4.
4. both dice show the same number.
a. P(at least one die shows 4) =
n(E)
n(S)
11
36
=
{(4,1), (4,2), (4,3), (4,4), (4,5),
(4,6), (1,4), (2,4), (3,4), (5,4),
(6,4)}
Solution:
b. P(both dice show the same number)
n(E)
n(S)
6
36
=
(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
=
1
6
or
Quiz: Answer the following questions involving probability of simple event.
Express your answer in lowest term.

28. ASSIGNMENT
The approach that I used was the interactive language activities like
writing and news casting. It is located at the additional activities or
remediation. (extend)
PERFORMANCE TASK:
The student will apply their knowledge on probability in some current
issues. They will create a news regarding the given topics below. They will
choose only one. The output will be presented the next class. They write
and record it on video form, news casting.
1. Covid-19 Pandemic
2. Climate Change and Extreme Weather Events.
3. Sports Analytics
4. Natural Disasters and Risk Assessment

29. ASSIGNMENT

30. Thank you for
listening!

31. ASSIGNMENT
A fair six-sided die is rolled. Find
the probability that the number is
i. even iv. even and a multiple of 3
ii. multiple of 3 v. an even number or multiple
iii. multiple of 5 of 5
Solution: Possible outcomes = {1, 2, 3, 4, 5, 6}
(i). even:P(even) = 3
6
or 1
2
(ii). multiple of 3:P(multiples of 3) = 2
6
or 1
3
(iii). multiple of 5:P(multiples of 5) = 1
6
ANSWER

32. ASSIGNMENT!
Solution: Possible outcomes = {1, 2, 3, 4, 5, 6}
(iv). even and a multiple of 3:
P(even and a multiple of 3) =
1
6
(v). an even or multiple of 5:
P(an even or multiple of 5) = 4
6
or 2
3