Embed presentation
Download to read offline




![Types of sets
Power set: from a set containing n element ,2n subsets can be formed . The
set consisting of these 2n subsets is called a power set.
Example: If A= {a,b}
P(S)=[{a},{b},{a,b},{ }]
Universal set: The set containing all elements or objects and of which all
other sets are subsets.
Symbol : U
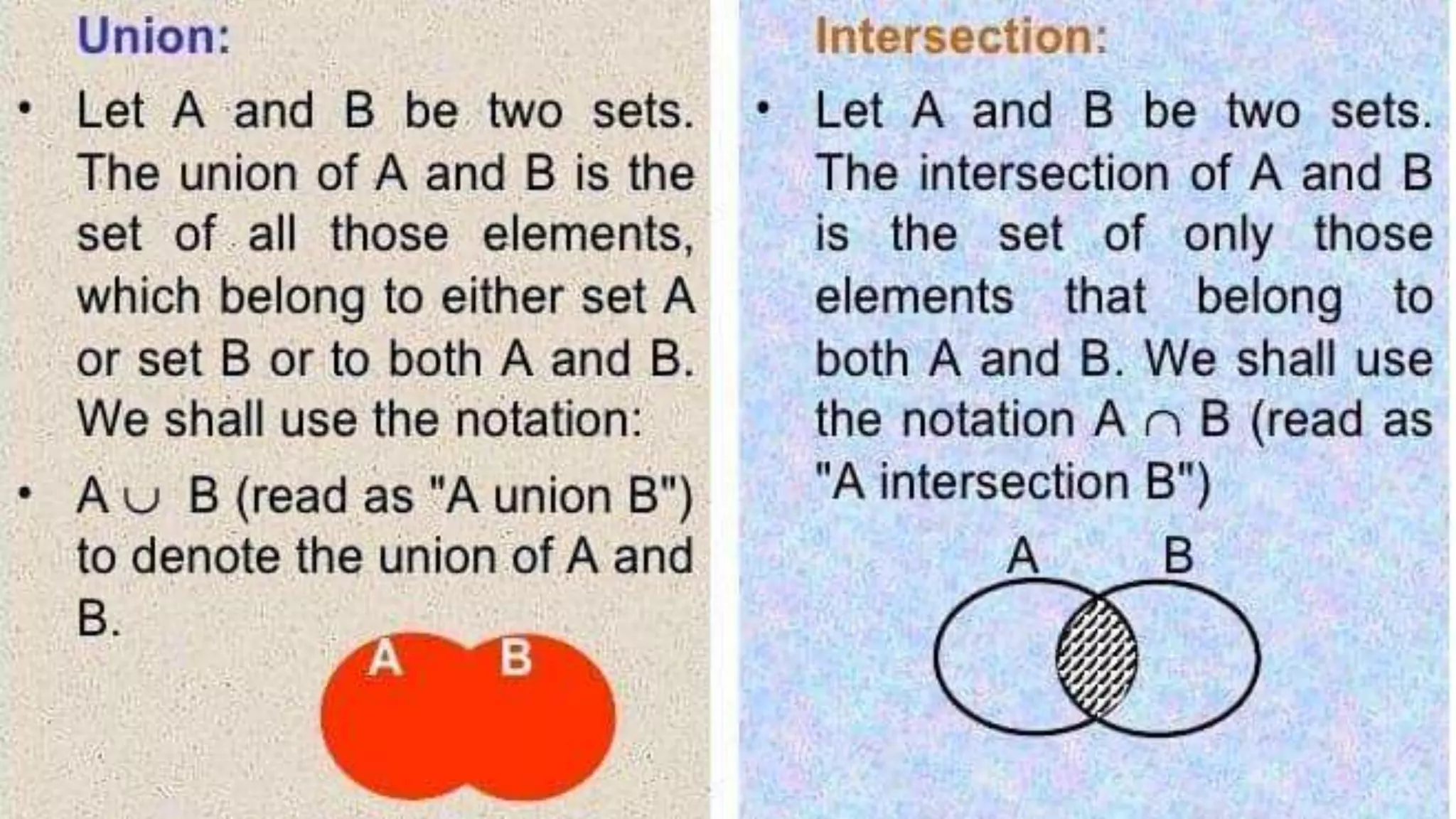
Venn Diagram: A ven diagram is a diagram
That shows all possible logical relations
Between a finite collection of different sets.](https://image.slidesharecdn.com/theoryofsets-190324180959/75/Theory-of-sets-5-2048.jpg)

This document defines and provides examples of different types of sets. It discusses finite and infinite sets, equal sets, empty sets, power sets, universal sets, and Venn diagrams. Finite sets can be counted, while infinite sets cannot. Two sets are equal if they contain the same elements. An empty set contains no elements. A power set contains all possible subsets of a set. A universal set contains all elements being considered. A Venn diagram visually depicts the logical relations between different sets.




![Types of sets
Power set: from a set containing n element ,2n subsets can be formed . The
set consisting of these 2n subsets is called a power set.
Example: If A= {a,b}
P(S)=[{a},{b},{a,b},{ }]
Universal set: The set containing all elements or objects and of which all
other sets are subsets.
Symbol : U
Venn Diagram: A ven diagram is a diagram
That shows all possible logical relations
Between a finite collection of different sets.](https://image.slidesharecdn.com/theoryofsets-190324180959/75/Theory-of-sets-5-2048.jpg)

