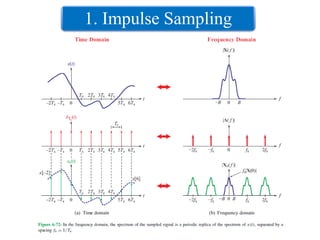
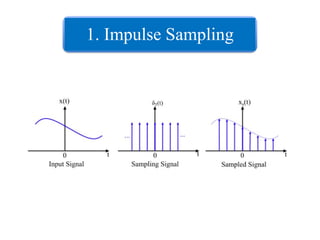
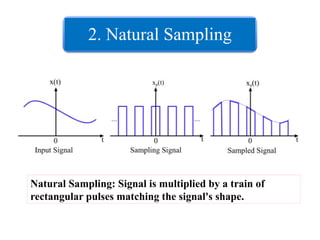
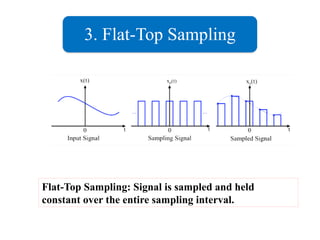
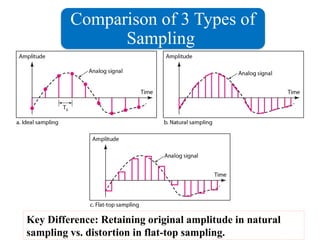
The document outlines the sampling theorem, which states that a signal can be reconstructed from its samples if sampled above the Nyquist rate. It discusses various sampling methods, including impulse, natural, and flat-top sampling, highlighting their differences and effects on signal quality. Additionally, it introduces band-pass sampling and its application in communication systems, with specific formulas for sampling frequencies.

1. Sampling
Theorem

2. • 1. Sampling
• - Sampling Theorem
• - Impulse Sampling
• - Natural and Flat-Top Sampling
• - Reconstruction of Signal from Samples
• - Aliasing and Effect of Under-Sampling
• - Introduction to Band-Pass Sampling
Table of Contents

3. • Definition: A signal can be exactly reconstructed from
its samples if it is sampled at a rate greater than twice
its highest frequency (Nyquist Rate).
• Formula: fs > 2fm
• Key Terms:
• - fs : Sampling frequency
• - fm: Maximum signal frequency
Sampling Theorem

4. 1. Impulse Sampling
2. Natural Sampling
3. Flat-Top Sampling
Types of Sampling

5. • Definition: Sampling where the signal is
multiplied by a periodic train of impulses.
• Equation: xs(t) = x(t) δ(t - nT)
⋅
1. Impulse Sampling

6. 1. Impulse Sampling

7. Natural and Flat-Top Sampling
• - Natural Sampling: Signal multiplied by a train of
rectangular pulses matching the signal's shape.
• - Flat-Top Sampling: Signal is sampled and held
constant over the sampling interval.
• - Key Difference: Retention of original amplitude
in natural sampling vs. distortion in flat-top
sampling.

8. 1. Impulse Sampling

9. 2. Natural Sampling
Natural Sampling: Signal is multiplied by a train of
rectangular pulses matching the signal's shape.

10. 3. Flat-Top Sampling
Flat-Top Sampling: Signal is sampled and held
constant over the entire sampling interval.

11. Comparison of 3 Types of
Sampling
Key Difference: Retaining original amplitude in natural
sampling vs. distortion in flat-top sampling.

12. • Method: Low-pass filtering to reconstruct the
continuous signal.
• Conditions: Sampling frequency must meet
the Nyquist Criterion.
Reconstruction of CT Signal from Samples

13. • Definition: Overlapping of spectral components
caused by under-sampling.
• Effect: Distortion in reconstructed signal.
Effect of Under Sampling:
Aliasing

14. Introduction to Band-Pass Sampling
• Extends the Nyquist theorem for band-pass signals.
• Condition: Sampling frequency depends on the signal
bandwidth, not its maximum frequency.
• Formula: fs > 2(B), where B is the bandwidth.
• Application: Communication systems.