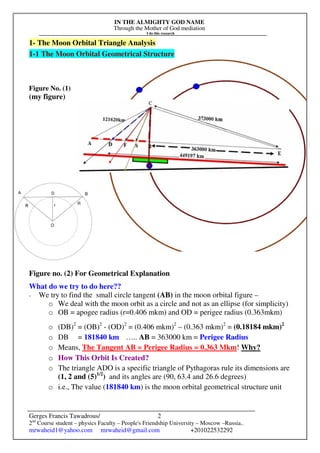
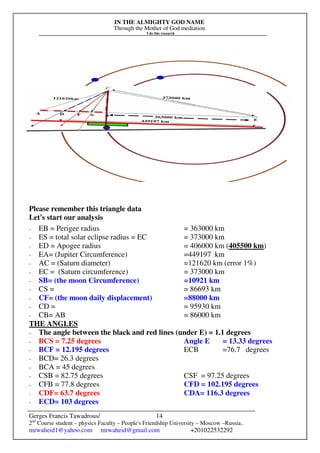
This document discusses the orbital geometry of the moon through multiple equations and figures. Some key points:
- The moon's orbit uses Pythagorean theorem, with the distance between perigee and apogee (43,000 km) as the base unit to create all other orbital distances.
- The 43,000 km distance is fundamental to the moon's orbital structure and motion, as it is used to concentrate energy into the orbit via Pythagorean relationships.
- Equations show the moon's creation and motion are related to light behavior, with an initial "supposed" light velocity of 1.16 mkm/sec that reduces to the known 0.3 mkm/sec after the moon