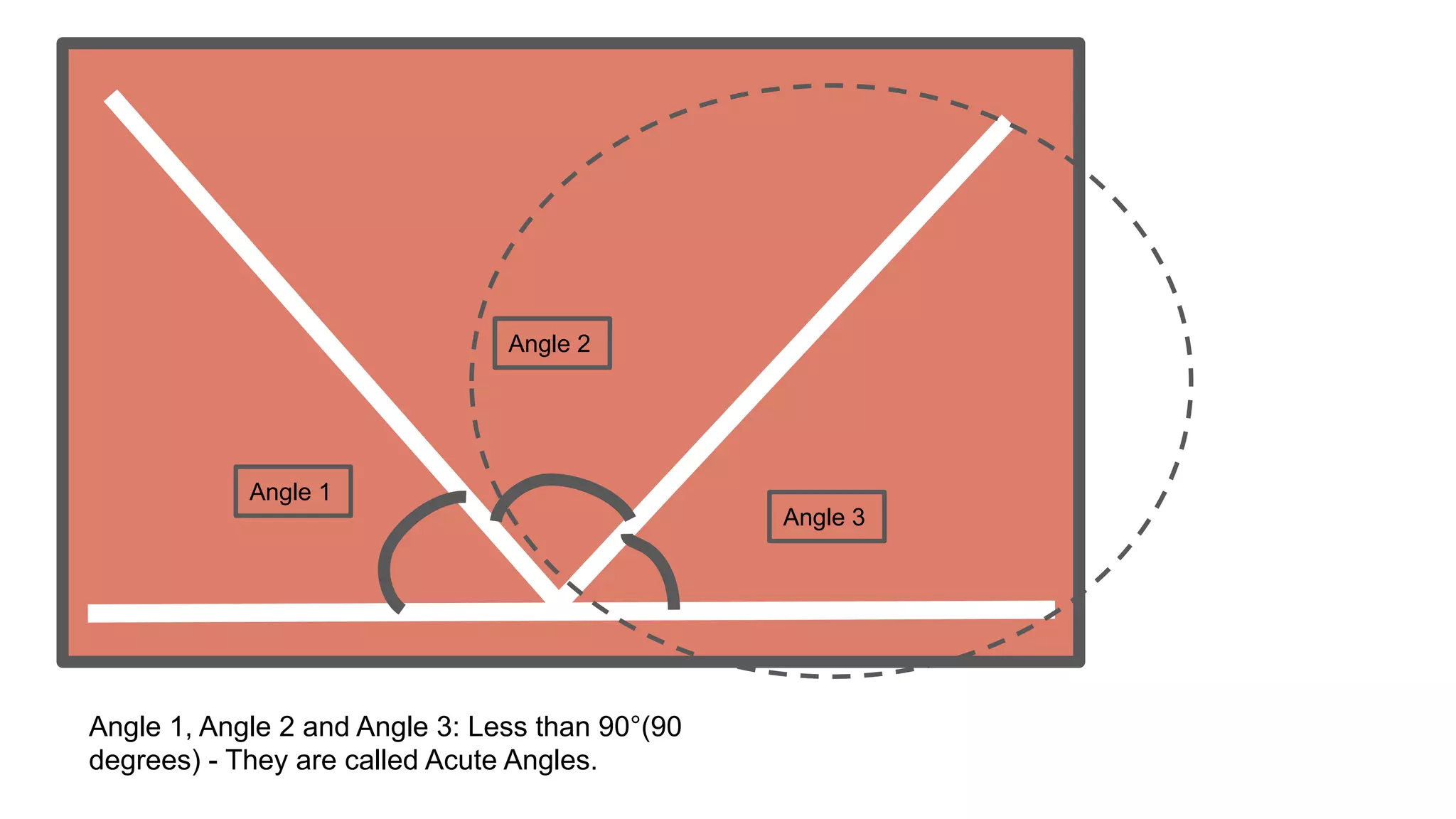
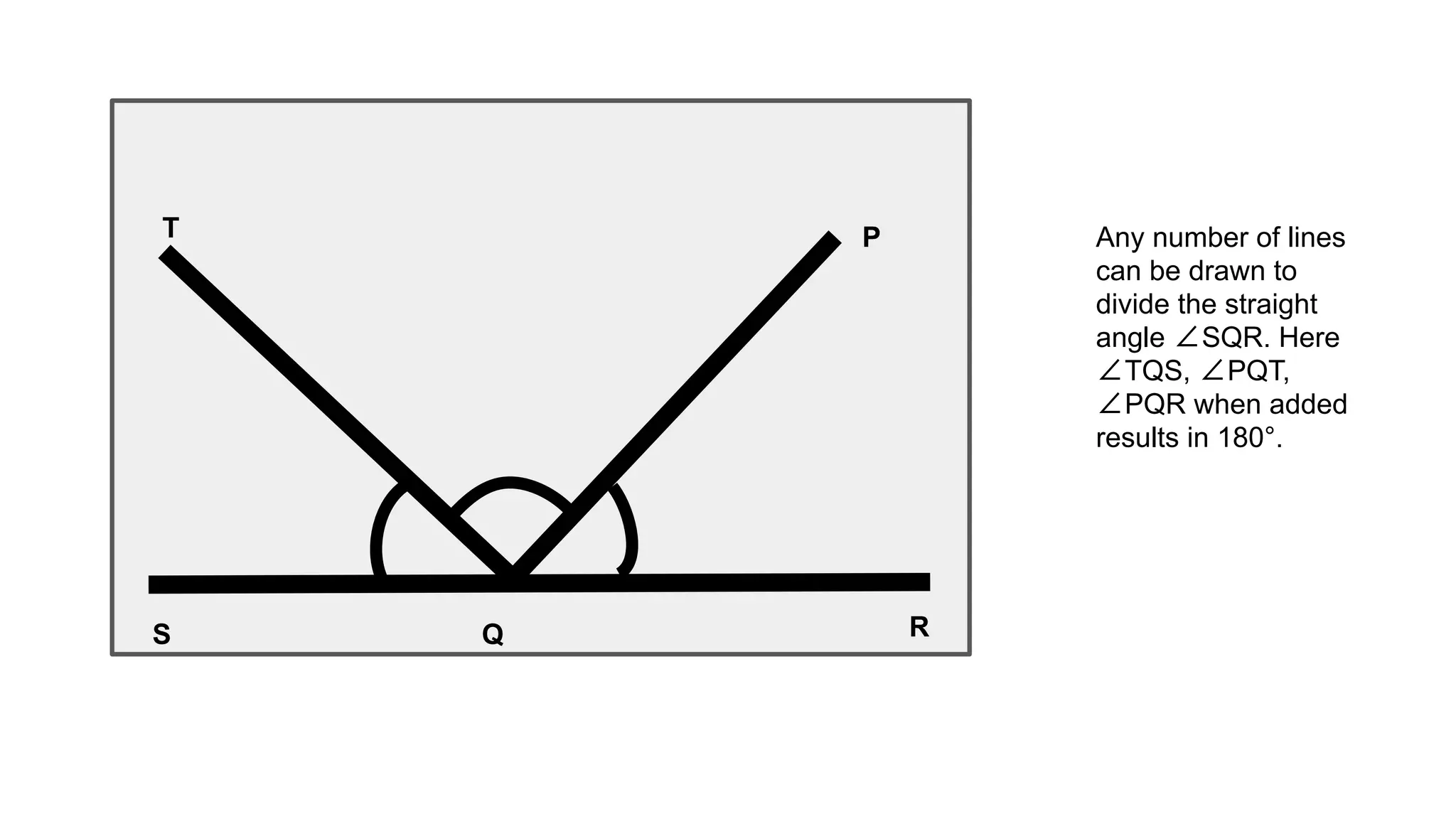
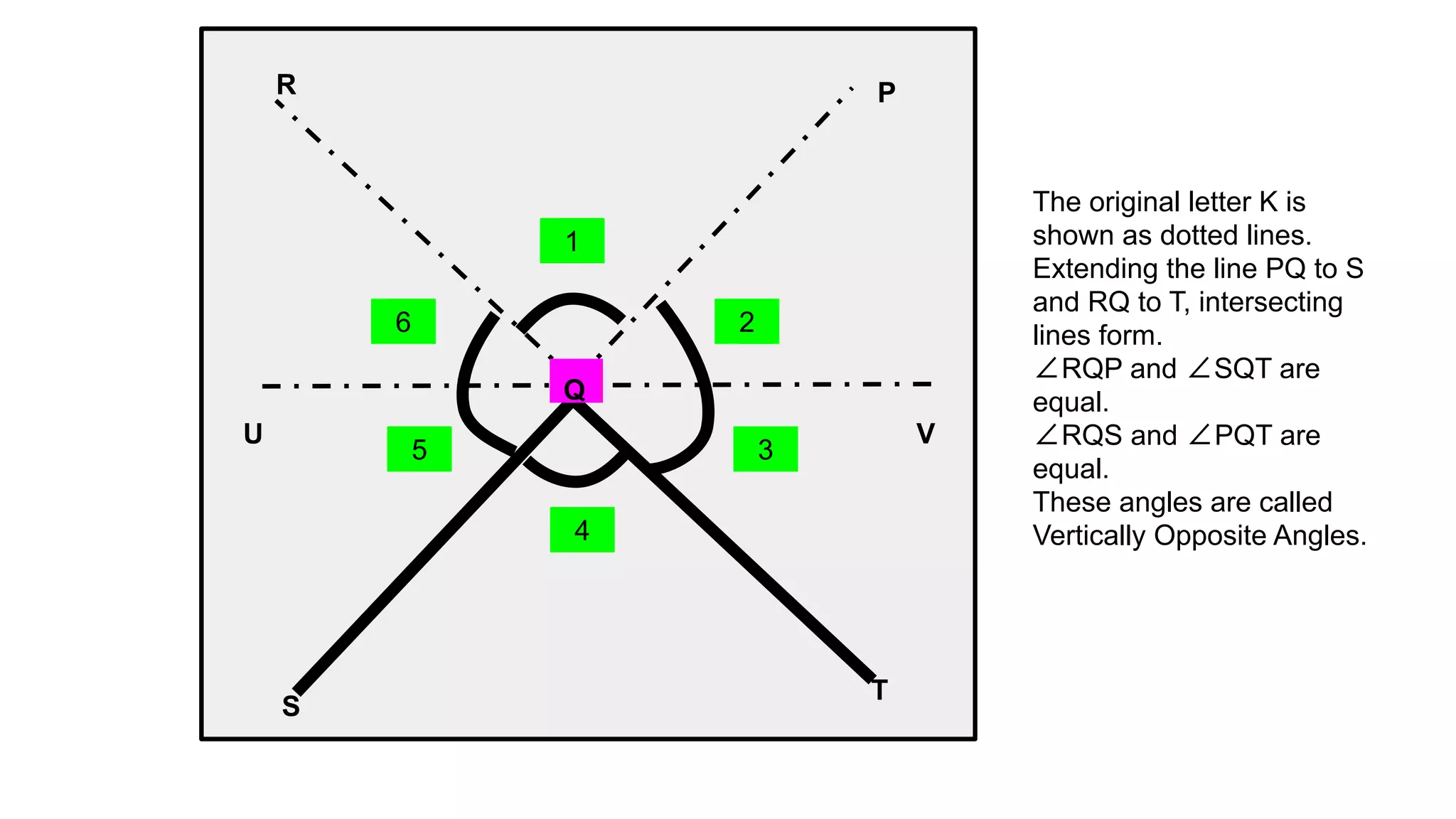
The K Method of Studying Angles uses the letter K to represent the main types of angles. Angle 1, 2 and 3 are acute angles that are less than 90 degrees. Adjacent angles are formed when a line divides an angle into two angles side by side. A right angle is equal to 90 degrees. Complementary angles and supplementary angles add up to 90 and 180 degrees respectively. An obtuse angle is larger than 90 degrees but less than 180 degrees. Vertically opposite angles are equal. A circular angle is equal to 360 degrees.

1. The K Method Of Studying
Angles
Authored By Adithya Ligory

2. The K Method of
Studying Angles
The letter K has all the
possible angles that you
need to know as a student!

3. Angle 1
Angle 2
Angle 3
Angle 1, Angle 2 and Angle 3: Less than 90°(90
degrees) - They are called Acute Angles.

4. P
Q R
S
RQ
P
Angles ∠PQR when
divided by a line SQ
results in two angles
side by side called
Adjacent Angles
(∠PQS and ∠SQR)

5. P
S
RQ
∠SQR is 90° (90
degrees) or it’s called
a Right Angle.
∠PQS and ∠PQR
when added results in
90°. They are called
Complementary
Angles.

6. P
S RQ
∠SQR is a straight line and
this is equal to 180°.
∠PQS and ∠PQR when
added results in 180°. They
are called Supplementary
Angles.
The angle ∠PQS is an
Obtuse Angle as it is larger
than 90°, but this angle is
less than 180°.

7. P
S RQ
T Any number of lines
can be drawn to
divide the straight
angle ∠SQR. Here
∠TQS, ∠PQT,
∠PQR when added
results in 180°.

8. PR
S
T
Q
U V
1
2
3
4
5
6
The original letter K is
shown as dotted lines.
Extending the line PQ to S
and RQ to T, intersecting
lines form.
∠RQP and ∠SQT are
equal.
∠RQS and ∠PQT are
equal.
These angles are called
Vertically Opposite Angles.

9. PR
S T
Equal vertical angles in
terms of angle size.
∠PQR and ∠SQT are
equal and are equal to 96°
(96 degrees)
∠RQS and ∠PQT are
equal to 84° (84 degrees)
Q

10. PR
S T
QU V
An angle that is 360° is
called a Circular Angle.
All angles shown here
add up to 360°.
∠RQU, ∠UQS,
∠SQT, ∠VQT, ∠PQV
and ∠PQR when
added together results
in 360°.