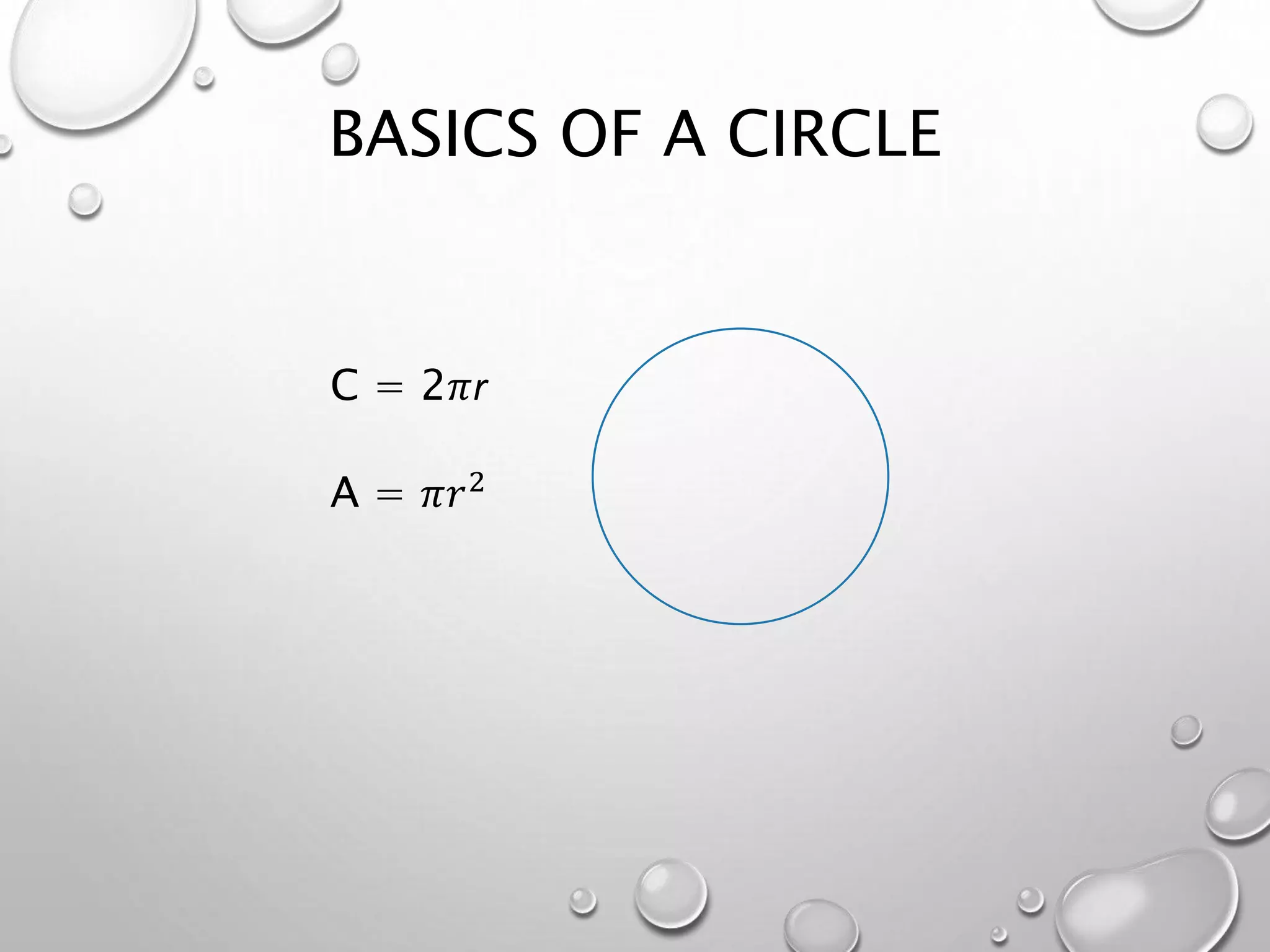
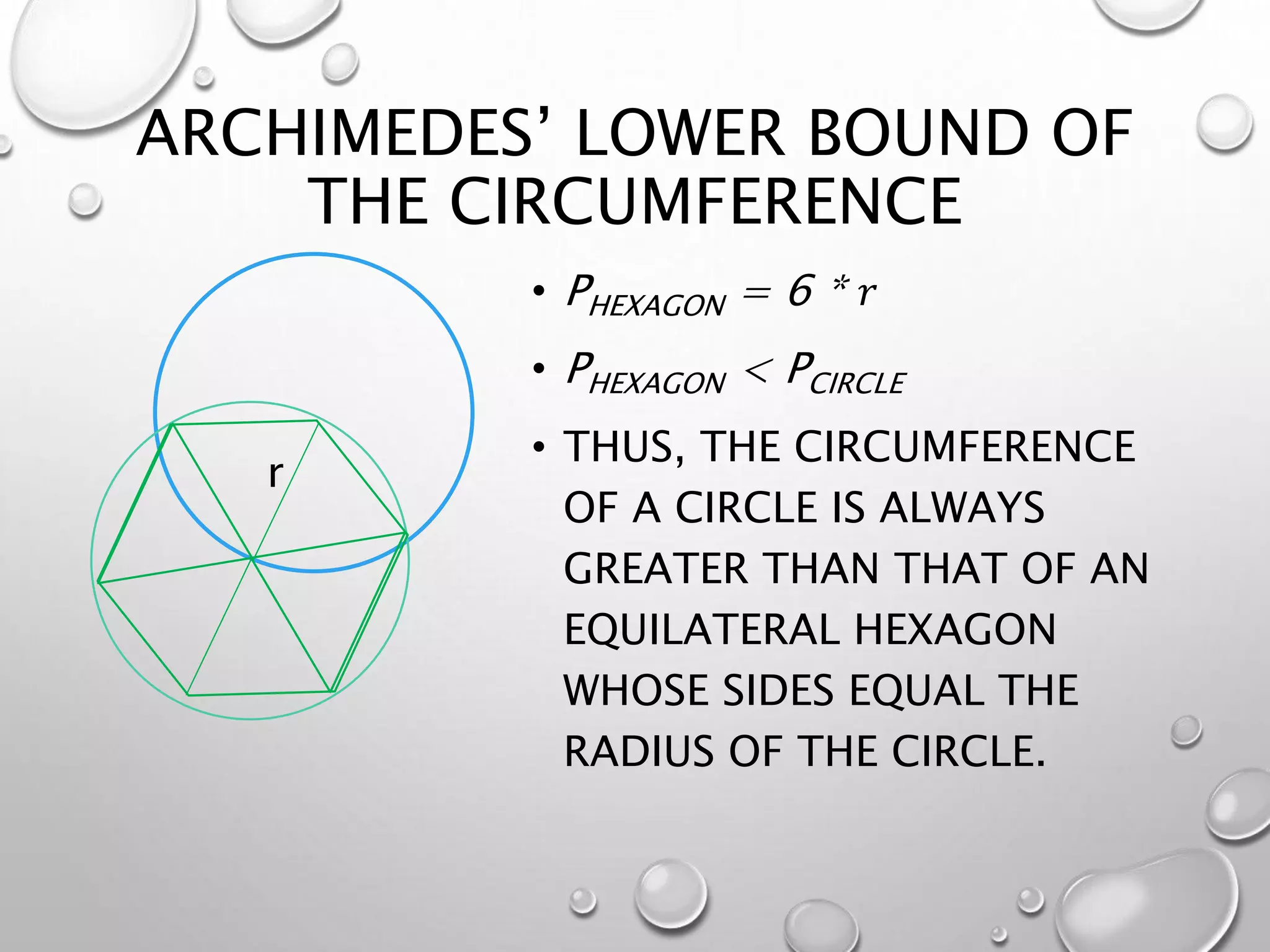
The document discusses the isoperimetric problem, which involves maximizing area while minimizing perimeter, illustrated through the legend of Queen Dido. It outlines historical contributions from mathematicians like Zenodorus and Pappus, who offered proofs related to shapes with equal perimeter and area. The author proposes to investigate deeper aspects of this problem in their honors thesis.

1. THE ISOPERIMETRIC
PROBLEM:
A PROPOSAL
BY: MIRIAM FELSENTHAL

2. DIDO’S PROBLEM
• THERE IS A LEGEND IN THE AENEID OF QUEEN
DIDO.
• SHE FLED TO NORTH AFRICA AND BARGAINED
WITH THE LOCAL RULER FOR A PLOT OF LAND
THAT A BULL’S HIDE CAN COVER.
• DIDO CUT THE HIDE INTO STRIPS AND
PROCEEDED TO LAY THEM OUT TO FORM A SEMI-
CIRCLE, THE SHAPE THAT WOULD ENCOMPASS
THE MOST TERRITORY, WHILE GAINING ACCESS
TO THE SEA.
• SHE APPARENTLY KNEW THE ANSWER TO THE

3. DIDO’S PROBLEM

4. THE ISOPERIMETRIC PROBLEM
• THE ISOPERIMETRIC PROBLEM IS THE CONCEPT
OF MAXIMIZING THE AREA WHILE MINIMIZING
THE PERIMETER.
• THROUGHOUT HISTORY, MANY
MATHEMATICIANS HAVE ENDEAVORED TO PROOF
THAT IT IS THE CIRCLE OF ALL THE SHAPES OF
EQUAL PERIMETER THAT HAS THE LARGEST AREA.
• I PROPOSE TO EXPLORE THE GENERAL TOPIC AND
THEN TO USE MY RESEARCH TO IDENTIFY A NEW
FACET TO THE ISOPERIMETRIC PROBLEM.

5. BASICS OF A CIRCLE
C = 2𝜋r
A = 𝜋𝑟2

6. ARCHIMEDES’ LOWER BOUND OF
THE CIRCUMFERENCE
• PHEXAGON = 6 * 𝑟
• PHEXAGON < PCIRCLE
• THUS, THE CIRCUMFERENCE
OF A CIRCLE IS ALWAYS
GREATER THAN THAT OF AN
EQUILATERAL HEXAGON
WHOSE SIDES EQUAL THE
RADIUS OF THE CIRCLE.
r

7. • THE LINE THAT DICTATES THE SHAPE OF A
SEMICIRCLE IS :
• 𝑦 = √(𝑟2
− 𝑥2
).
• TO EVALUATE THE AREA, IT IS NECESSARY TO
TAKE THE INTEGRAL FROM ONE END OF THE
SHAPE TO THE OTHER.
• THE SOLUTION TO THIS INTEGRAL IS:
• 𝐴 𝑠𝑒𝑚𝑖−𝑐𝑖𝑟𝑐𝑙𝑒 = 𝜋𝑟2
2
• DOUBLING THIS FORMULA APPLIES IT TO A
CIRCLE:
CALCULUS APPROACH

8. TWO FUNDAMENTALS OF THE
ISOPERIMETRIC PROBLEM
• STATEMENT 1: AMONG ALL SHAPES OF THE SAME
PERIMETER, THE CIRCLE HAS THE LARGEST AREA.
• STATEMENT 2: AMONG ALL SHAPES OF THE SAME
AREA, THE CIRCLE HAS THE SMALLEST
PERIMETER.

9. PROOF BY CONTRADICTION
• ASSUME THAT STATEMENT 1 IS TRUE, BUT
STATEMENT 2 IS FALSE.
C F
C’
• AC = AF
• PC > PF
• PC’ = PF
• AC’ < AC → AC’ < AF

10. ZENODORUS
• GREEK MATHEMATICIAN FROM THE SECOND
CENTURY BCE.
• ON ISOPERIMETRIC FIGURES
• THEON OF ALEXANDRIA AND PAPPUS (FOURTH
CENTURY CE)
• HE CLAIMED TO HAVE DEVELOPED A PROOF
THAT THE SHAPE THAT IS EQUILATERAL AND
EQUIANGULAR IS THE GREATEST OF ALL SHAPES
THAT HAVE AN EQUAL NUMBER OF SIDES AND
EQUAL PERIMETER.

11. FIRST LEMMA
• PSCALENE = PISOSCELES
• ACALENE < AISOSCELES
• IF AN ISOSCELES TRIANGLE AND A SCALENE
TRIANGLE SHARE THE SAME BASE AND HAVE EQUAL
PERIMETERS, THE AREA OF THE ISOSCELES
TRIANGLE WILL BE LARGER.

12. SECOND LEMMA
• WHEN THERE ARE TWO NON-SIMILAR ISOSCELES
TRIANGLES WITH A GIVEN SUMMED PERIMETER AND
SUMMED AREA, IF ONE WERE TO CONSTRUCT
SIMILAR ISOSCELES TRIANGLES ON THE RESPECTIVE
BASES OF THE FIRST TWO SO THAT THE SUM OF
THEIR PERIMETERS IS EQUAL TO THOSE OF THE
ORIGINALS, THE SUM OF THE AREA OF THE SIMILAR
TRIANGLES WILL BE GREATER THAN THAT OF THE
NON-SIMILAR TRIANGLES.
C D
A B

13. ZENODORUS’ PROOF: PART 1
• ACCORDING TO THE FIRST
LEMMA, AAFC > AABC
C
D
A
B
E
F
• THUS, THE AREA OF THE
PENTAGON WOULD BE
LARGER IF ALL OF ITS SIDES
WOULD BE EQUILATERAL.
• AF + FC = AB + BC
AND ABC IS A SCALENE ONE.
• AFC IS AN ISOSCELES
TRIANGLE,

14. ZENODORUS’ PROOF: PART 2
• P ABC + CDE = P AFC + CGE.
C
D
A
B
E
F
G
• ABC AND CDE ARE NON-SIMILAR
ISOSCELES TRIANGLES.
• DRAW AFC AND CGE SUCH THAT
THEY ARE SIMILAR ISOSCELES
TRIANGLES.
• ACCORDING TO THE SECOND
LEMMA,
• A ABC + CDE < A AFC + CGE.• THUS, THE AREA OF THE
PENTAGON WOULD BE LARGER IF
ALL OF ITS SIDES WOULD BE
EQUIANGULAR.

15. PAPPUS
• “BEES, THEN, KNOW JUST THIS FACT WHICH IS USEFUL TO
THEM, THAT THE HEXAGON IS GREAT[EST]…AND WILL
HOLD MORE HONEY FOR THE SAME EXPENDITURE OF
MATERIAL IN CONSTRUCTING EACH. BUT WE, CLAIMING A
GREATER SHARE IN WISDOM THAN THE BEES, WILL
INVESTIGATE A SOMEWHAT WIDER PROBLEM, NAMELY
THAT, OF ALL EQUILATERAL AND EQUIANGULAR PLANE
FIGURES HAVING AN EQUAL PERIMETER, THAT WHICH HAS
THE GREATER NUMBER OF ANGLES IS ALWAYS GREATER,
AND THE GREATEST OF THEM ALL IS THE CIRCLE HAVING
ITS PERIMETER EQUAL TO THEM.”

16. FURTHER EXPLORATION OF THE
ISOPERIMETRIC PROBLEM
• PAPPUS PROPOSED THAT THE SEMI-CIRCLE WILL
HAVE THE LARGEST AREA OF ALL CIRCULAR
SEGMENTS THAT HAVE THE SAME
CIRCUMFERENCE.
• JAKOB STEINER, IN 1838, PRESENTED FIVE
PROOFS ON THE SUBJECT, YET THEY ALL ASSUME
THE EXISTENCE OF A SOLUTION, WHICH RENDERS
THEM UNSUITABLE AS RIGOROUS MATHEMATICAL
PROOFS.
• KARL WEIERSTRASS, IN 1879, FINALLY PRESENTED
A PROPER SOLUTION, THROUGH THE USE OF

17. ISOPERIMETRIC PROBLEM
• THE ISOPERIMETRIC PROBLEM DEALS WITH
MAXIMIZING AREA AND MINIMIZING PERIMETER.
• ISOPERIMETRIC INEQUALITY:
• ISOPERIMETRIC QUOTIENT:
• N-DIMENSIONS

18. MY PROPOSAL
• IN MY HONORS THESIS PAPER, I PLAN TO
EXPLORE THESE TOPICS AND CULTIVATE A
RICHER UNDERSTANDING AS TO THE
MATHEMATICS BEHIND THIS HISTORICAL
CHALLENGE.

19. End of slideshow, click to exit.