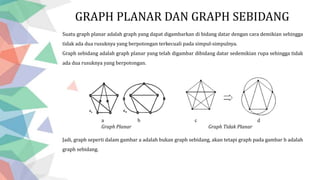
Dokumen ini membahas konsep graph planar dan graph sebidang, termasuk definisi serta rumus Euler yang menghubungkan jumlah simpul, rusuk, dan daerah. Ditegaskan bahwa p - q + r = 2 untuk graph sebidang terhubung, beserta ketidaksamaan yang menjelaskan sifat planar dari graph. Contoh-contoh dari berbagai graph juga diberikan untuk mendukung teori-teori yang diuraikan.

2. Nama Kelompok
1 Annisa Karima Rafiana
2
3
4
Atika Ayu Prameswari
Oktavia Yusni Kurniasih
Swastyka Rahma Wiyanti
4 Rita Nurkhalipah
5 Swastyka Rahma Wiyanti

3. GRAPH PLANAR DAN GRAPH SEBIDANG
Suatu graph planar adalah graph yang dapat digambarkan di bidang datar dengan cara demikian sehingga
tidak ada dua rusuknya yang berpotongan terkecuali pada simpul-simpulnya.
Graph sebidang adalah graph planar yang telah digambar dibidang datar sedemikian rupa sehingga tidak
ada dua rusuknya yang berpotongan.
Jadi, graph seperti dalam gambar a adalah bukan graph sebidang, akan tetapi graph pada gambar b adalah
graph sebidang.
a b
Graph Planar
c d
Graph Tidak Planar

4. GRAPH PLANAR DAN GRAPH SEBIDANG
Potongan-potongan bidang terhubung disebut daerah (region). Simpul-simpul dan rusuk yang bertemu
dengan daerah R membangun suatu batas dari R.
Pada graph G1 mempunyai 3 daerah, graph G2 mempunyai 1 daerah, dan G3 mempunyai 6 daerah.
Batas- batas daerah R1 di G3 terdiri atas simpul-simbul b,c, dan d dan rusuk-rusuk bc,bd, dan cd ; batas-
batas daerah R6 terdiri atas simpul-simpu a,b,c,e,f, dan g dan rusuk-rusuk ab, bc, ce, ef, fg, dan gb.
Daerah R6 disebut daerah luar dari G3. Setiap graph sebidang senantiasa mempunyai satu daerah.
Graph sebidang G1 mempunyai p = 4 simpul, q = 5 rusuk, dan r = 3 daerah ; G3 mempunyai p =7 , q = 11,
dan r = 6. Perhatikan bahwa dalam ketiga kasus itu berlaku p – q + r = 2.

5. RUMUS EULER DAN PERLUASANNYA
Teorema 5.1 (Rumus Euler)
Jika G (p,q) adalah graph sebidang terhubung yang r daerah , maka p – q + r = 2
Catatan :
Graph G(p,q) bidangterhubung adalah syarat perlu untuk p – q + r = 2. Tetapi bukan syarat perlu dan
cukup. Jadi, jika berlaku p – q + r = 2, belum tentu graph G(p,q) sebidang terhubung.
Hubungan antara jumlah titik (p), jumlah sisi (q), dan jumlah wilayah (r) pada graf bidang:
p – q + r = 2 (Rumus Euler)
Pada Gambar di atas, q = 11 dan p = 7, r = ?,
Jadi 7 - 11 + r = 2, maka r = 6.
R1
R2
R3
R5
R4
R6

6. RUMUS EULER DAN PERLUASANNYA
Teorema 5.2
Jika G adalah graph sebidang terhubung dengan banyak simpul p, p > 3, dan banyak rusuk q, maka q ≤
3p – 6.
Catatan :
Kontra positif dari teorema ini adalah, jika q ≥ 3p – 6, maka graph G(p,q) tidak terhubung planar.
Konversnya belum tentu benar ; artinya, jika dalam graph G(p,q) berlaku q ≤ 3p – 6, maka G(p,q) beum
tentu planar terhubung.
Contoh:
Pada K4, p = 4, q = 6, memenuhi ketidaksamaan Euler, sebab 6 3(4) – 6. Jadi, K4 adalah graf planar.

7. RUMUS EULER DAN PERLUASANNYA
Teorema 5.3 Graph Bipartit K5 adalah non planar
Pada graf K5, p = 5 dan q = 10, tidak memenuhi ketidaksamaan Euler sebab
10 3(5) – 6. Jadi, K5 tidak planar

8. RUMUS EULER DAN PERLUASANNYA
Teorema 5.4 Graph lengkap K3,3 adalah nonplanar
Ketidaksamaan q ≤ 3p – 6 tidak berlaku untuk K3,3
karena
q = 9, p = 6
9 ≤ (3)(6) – 6 = 12 (jadi, q ≤ 3p – 6)
padahal graf K3,3 bukan graf planar!

9. RUMUS EULER DAN PERLUASANNYA
Teorema 5.5
Setiap graph planar G memuat suatu simpul v sedemikian rupa sehingga deg v<5
Bukti :
Jika G hanya memiliki satu simpul, simpul ini harus memiliki derajat 0. Jika G hanya memiliki dua
simpul maka keduanya harus memiliki derajat paling banyak 1. Dengan demikian dapat di duga
bahwa p ≥ 3, yaitu, bahwa G setidaknya memiliki tiga simpul.
Sekarang jika derajat untuk setiap simpul dari G adalah setidaknya enam dimiliki
Namun, dengan Teorema 𝑣∈𝑉 𝑑 𝑣 = 2𝑞. Jadi 2q ≥ 6p dan q ≥ 3p karena ini tidak mungkin,
menurut teorema 5.2, q ≤ 3p - 6. Kontradiksi ini menunjukkan bahwa G harus memiliki setidaknya satu
simpul dari derajat yang kurang dari sama dengan 6. Tidak semua simpul dapat berderajat 6 atau lebih,
sehingga terdapat suatu simpul v dengan deg v < 5.

10. Thank you