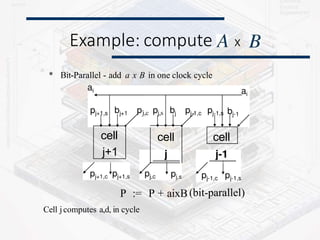
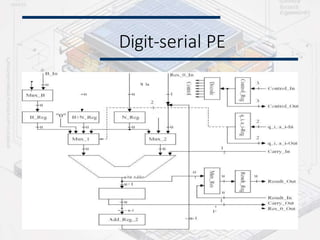
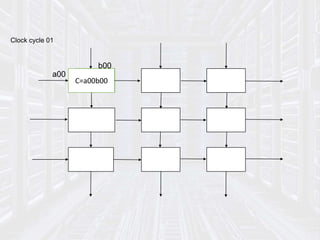
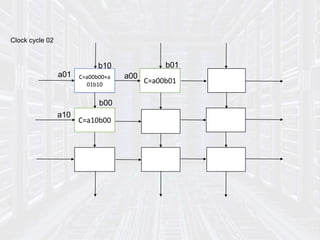
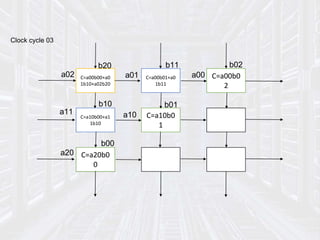
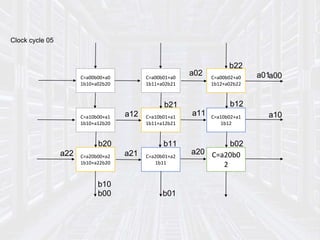
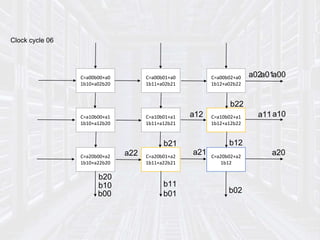
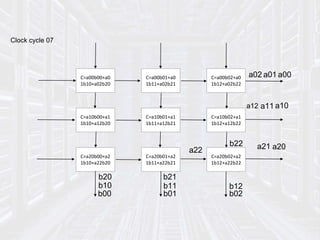
Systolic arrays are parallel processing architectures that leverage a rhythmic data flow to perform computations efficiently using a network of identical processing elements with local connections. This architecture is particularly suited for applications requiring high data throughput and minimizing memory access, distinguishing itself from von Neumann architectures by relying on synchronous data transfers and providing significant parallelism. Modern implementations of systolic arrays can be found in Google's Tensor Processing Unit, NVIDIA's tensor cores, and MIT's Eyeriss architecture, all designed to accelerate machine learning and AI workloads.

1. SYSTOLIC ARRAY ARCHITECTURE

2. SYSTOLIC ARRAYS
* A class of parallel processors, named after the data flow through the array,
analogous to the rhytmic flow of blood through human arteries after each
heartbeat.
* The concept of systolic processing combines a highly parallel array of
identical processor may span several integrated circuit chips.
* A set of simple Processing Elements with regular and local connections takes
external inputs and processes term in a predetermined manner in a pipelined
fashion.

3. ARCHITECTURE
• A systolic array typically consists of a large monolithic network of primitive computing
nodes which can be hardwired or software configured for a specific application.
• The nodes are usually fixed and identical, while the interconnect is programmable.
• The more general wavefront processors, by contrast, employ sophisticated and
individually programmable nodes which may or may not be monolithic, depending on the
array size and design parameters.
• The other distinction is that systolic arrays rely on synchronous data transfers, while
wavefront tend to work asynchronously.

4. ARCHITECTURE
• In Von Neumann architecture, the program execution follows a script of instructions
stored in common memory, addressed are sequenced under the control of the CPU's
program counter (PC)
• The individual nodes within a systolic array are triggered by the arrival of new data and
always process the data in exactly the same way.
• The actual processing within each node may be hard wired or block microcoded, in which
case the common node personality can be block programmable.
• The systolic array paradigm with data-streams driven by data counters, is the counterpart
of the Von Neumann architecture with instruction-stream driven by a program counter.
• Because a systolic array usually sends and receives multiple data streams, and multiple
data counters are needed to generate these data streams, it supports data parallelism.

5. SYSTOLIC ARRAYS
• In a systolic array, there are a large number of identical simple processors or
processing elements(PEs) that are arranged in a well-organized structure such as a
linear or two-dimensional array.
• Each processing element is connected with the other PEs and has limited private
storage.
• Replace single processor with array of regular Processing Elements.
• Orchestrate data flow for high throughput with less Memory access.
'
PE

6. SYSTOLIC ARCHITECTURE
• Basic principle: Replaces a single PE with a regular array of PEs and carefully
orchestrate flow of data between the PEs Balance computation and memory
bandwidth INSTEAD OF 5 MILLION OPERATIONS PER SECOND
• Differences from pipelining: These are individual PEs figures Array structure can
be non-linear and multi-dimensional PE connections can be multidirectional (and
different speed)
• PEs can have local memory and execute kernels (rather than a piece of the
instruction)

7. SYSTOLIC ARRAY CONFIGURATIONS
Fir-filter, convolution, discrete Fourier
transform (DFT), solution of triangular
linear systems, carry pipelining, cartesian
product, odd- even transportation sort,
real-time priority queue, pipeline arithmetic
units.
Dynamic programming for optimal
parenthesization, graph algorithms
involving adjacency matrices.

8. Matrix arithmetic (matrix multiplication, L-U
decomposition by Gaus- sian climination
without pivoting. QR-factorization),
transitive closure, pattern match. DFT,
relational database operations.
Searching algorithms (queries on nearest
neighbor, rank, etc., systolic search tree),
parallel function evaluation, recurrence
evaluation.
Inversion of triangular matrix, formal
language recognition.

9. Systolic Array
3 x 3 Matrix Multiplication

10. 3 x 3 Matrix
• A =
𝑎00 𝑎01 𝑎02
𝑎10 𝑎11 𝑎12
𝑎20 𝑎21 𝑎22
• B =
𝑏00 𝑏01 𝑏02
𝑏10 𝑏11 𝑏12
𝑏20 𝑏21 𝑏22
c =
a00b00 + a01b10 + a02b20 a00b01 + a01b11 + a02b21 a00b02 + a01b12 + a02b22
a10b00 + a11b10 + a12b20 a10b01 + a11b11 + a12b21 a10b02 + a11b12 + a12b22
a20b00 + a21b10 + a22b20 a20b01 + a21b11 + a22b21 a20b02 + a21b12 + a22b22
𝑡𝑖𝑚𝑒 = 3 ∗ 𝑛 − 2
For n x n mesh

11. Clock cycle 00

12. Clock cycle 01
C=a00b00
a00
b00

13. Clock cycle 02
C=a00b00+a
01b10
C=a00b01
C=a10b00
a01
b10
a10
b00
a00
b01

14. Clock cycle 03
C=a00b00+a0
1b10+a02b20
C=a00b01+a0
1b11
C=a00b0
2
C=a10b00+a1
1b10
C=a10b0
1
C=a20b0
0
a02
b20
a11
b10
a01
b11
a00
b02
a10
b01
a20
b00

15. Clock cycle 04
C=a00b00+a0
1b10+a02b20
C=a00b01+a0
1b11+a02b21
C=a00b02+a0
1b12
C=a10b00+a1
1b10+a12b20
C=a10b01+a1
1b11
C=a10b0
2
C=a20b00+a2
1b10
C=a20b0
1
a12
b21
a02 a01 a00
b12
a11
b11
a21
b20
b10
b00
a10
b02
a20
b01

16. Clock cycle 05
C=a00b00+a0
1b10+a02b20
C=a00b01+a0
1b11+a02b21
C=a00b02+a0
1b12+a02b22
C=a10b00+a1
1b10+a12b20
C=a10b01+a1
1b11+a12b21
C=a10b02+a1
1b12
C=a20b00+a2
1b10+a22b20
C=a20b01+a2
1b11
C=a20b0
2
a12
b21
a02 a01a00
b22
a11
b11
a22
b20
b10
b00
a10
b02
a20
b01
b12
a21

17. Clock cycle 06
C=a00b00+a0
1b10+a02b20
C=a00b01+a0
1b11+a02b21
C=a00b02+a0
1b12+a02b22
C=a10b00+a1
1b10+a12b20
C=a10b01+a1
1b11+a12b21
C=a10b02+a1
1b12+a12b22
C=a20b00+a2
1b10+a22b20
C=a20b01+a2
1b11+a22b21
C=a20b02+a2
1b12
a02a01a00
b22
a22
b20
b10
b00
a12 a11a10
b12
a21
b21
b11
b01
a20
b02

18. Clock cycle 07
C=a00b00+a0
1b10+a02b20
C=a00b01+a0
1b11+a02b21
C=a00b02+a0
1b12+a02b22
C=a10b00+a1
1b10+a12b20
C=a10b01+a1
1b11+a12b21
C=a10b02+a1
1b12+a12b22
C=a20b00+a2
1b10+a22b20
C=a20b01+a2
1b11+a22b21
C=a20b02+a2
1b12+a22b22
a02 a01 a00
b22
a22
b20
b10
b00
a12 a11 a10
b12
a21
b21
b11
b01
a20
b02

19. ■ y1 = w1x1 + w2x2 + w3x3
■ y2 = w1x2 + w2x3 + w3x4
■ y3 = w1x3 + w2x4 + w3x5
Figure Design W1: systolic
convolution array (a) and cell (b)
where w;'s stay and x;'s and y's move
systolically in opposite directions.
Figure Overlapping the executions of
multiply and add in design W1.
Systolic Computation Example: Convolution
■Worthwhile to implement adder and
multiplier separately to allow
overlapping of add/mul executions

20. COMBINATIONS
 Combinations Systolic arrays can be
chained together to form powerful
systems
 This systolic array is capable of
producing on-the-fly least-squares fit to
all the data that has arrived up to any
given moment

21. GENERIC SYSTOLIC ARRAYS
* In Generic Systolic Arrays; processing units are connected in
linear array. Each cell is connected with its immediate
neighbours; each cell can exchange data and results with the
outside. Furthermore, each cell can receive data from the top
and transmit result to the bottom. (The WARP machine can be
viewed as GSA of size 10)
* It is also to possible to obtained 2-dimensional arrays by
stacking several linear arrays and adequately connecting
channels together. Other topologies (Ring, Cylinder, Torrus)
can be obtained in a similar way.

22. GENERIC SYSTOLIC ARRAYS
U1 RL; 1
RU
LR2 LR
Dt
R
RLn-1
D,
LR,+1 LRn
*n
RLn
LRn 1
”
Dn
* Cell P, admits three input channels; P, can receive data from Pi through
Channel LQ (Left to Right), from P,ql through RL;, and from the outside
through U,(Up).
* P, has also three output channels, which allow transmission of results to
the left and right neighbours and to the outside.

23. RL 1
LR;
GENERIC SYSTOLIC ARRAYS
B[i] C[i]
A[i]
RL,
LR„,

24. GENERIC SYSTOLIC ARRAYS
* The internal memory of cell PE contains six communica-tions
registers, denoted A[i], B[i],C[i], E[i], F[j] and G[i] .The remaining part of the
memory is denoted M[i] its size is independent from the size n of
the network.
* The program executed by every cell is a loop, whose body is
finite, partially ordered by set of statement that specify three
kinds of actions
• values (data) from some input channels,
• Performing computations within the internal memory
• Transmitting values (results) to output channels.

25. GENERIC SYSTOLIC ARRAYS
* The processing units acts with high synchronism (often
provided by a global, broadcasted clock). But this can lead
to implementation problems.
* Another solution is ie synchronization by communication,
named rendezvous. Value can be transmitted from a cell to
another only when both cells are prepared to do so.
* During communication phase, only input registers A, C and
G are changed; during computatian phase, only storage
register M and ie. output registers B, E and F are changed.

26. SPACE-TIME METHODOLOGY
* The algorithms to be mapped is specified as a set of
equations attached to integral points, and mapped on the
architecture using a regular time and space allocation
scheme.
* Four main steps using this methodology:
• The index localization (computations to be performed are
defined by equation).
• Uniformization (indicating where data need to be and where the
results are being produced).
• Space-Time Transformation (a time and a processor allocations
functions are being chosen).
• Interface Design (the loading of the data and the unloading of the
results are considered).

27. SPACE-TIME METHODOLOGY
• The drawbacks of Space Time Methodology:
 The algorithm must be specified as a set of
recurrence equation, or nested do-loop instructions.
Difficult to implement.
 Location in space is associated to each index value
(well suited for systhesis of regular arrays in which
data will be introduced in a regular order). Eliminates
possibility of synthesizing with other architectures.

28. SYSTOLIC ARRAYS: PROS AND CONS
• Advantages:
Principled  Efficiently makes use of limited memory bandwidth,
balances computation to I/O bandwidth availability Specialized
(computation needs to fit PE organization/functions)
 improved efficiency, simple design, high concurrency/
performance
 good to do more with less memory bandwidth requirement
• Downside:
Specialized → not generally applicable because computation
needs to fit the PE functions/organization

29. SYSTOLIC ARCHITECTURES
• Bit-serial architecture
⁘ processes one input bit during a clock cycle. Is well
suited for low speed applications.
• Bit-parallel architecture
⁘ processes one input word during a clock cycle. Well
suited for high-speed applications, but is area-inefficient
• Digit-serial architecture
⁘ attempts to utilize ie best of bo1 worlds. The speed of bit-
parallel and the relative simplicity of bit-serial.

30. Example: compute
* Use n digit multipliers to form o,xB and
add to a partial product P:
P : = 0 ;
For i : = n- 1 down to 0 do
P := rxP + aixB
Result: P - AxB
x

31. Example: compute x
* Bit-serial - addition of xB over o cycles
a, a a, time
j-1
wk
«r
carry
time
j+1 carry
time
j •«r
‹
›
;
+
P := P + a; xB
Cell j computes a,b in cycle
(bit-serial)

32. Example: compute x
* Bit-Parallel - add a x B in one clock cycle
j,c ,s
cell cell
cell
j+1
P := P + aixB
Cell jcomputes a,d, in cycle
(bit-parallel)

33. FA
FA
PE for Montogmery
B0b,0.. * At ith step, the term AiB+QiN
is computed in the upper part.
Results are shifted,
accumulated in ie lower part
• Calculations in first n cycles
* Output in next n cycles
* Zero bit interleaving enables
synchronization with the next
iteration of the algorithm

34. Digit-serial PE
N In

35. Digit-serial implementation
• Width of processing elements is u
• Only need it/u instead of x processing elements
⁘ N reg [u bits): storage of the modulus
⁘ B-reg (x bits): storage of the B multiplier
o B+N-reg (u bits): storage of intermediate result
o B+N Add-reg (x+1 bits): storage of intermediate
results
⁘ Control-reg (3 bits): multiplexer control/clock enable
⁘ Result-reg u bits): storage of the result

36. EXAMPLES OF MODERN SYSTOLIC ARRAY
Google's Tensor Processing Unit (TPU): Google's TPU is a
custom ASIC designed specifically for accelerating
machine learning workloads, particularly neural network
computations. The TPU utilizes a systolic array
architecture to perform matrix multiplications efficiently,
which are at the core of many deep learning algorithms.
NVIDIA's Tensor Cores: NVIDIA's Tensor Cores, introduced in
their Volta and later GPU architectures, employ a systolic array
design to accelerate matrix multiplication operations for deep
learning and AI applications. These specialized units provide
significant performance improvements for tensor operations
commonly used in neural networks.

37. EXAMPLES OF MODERN SYSTOLIC ARRAY
MIT's Eyeriss Architecture: Eyeriss is a systolic array-based
accelerator architecture for convolutional neural networks (CNNs),
developed by researchers at MIT. It aims to provide high energy
efficiency and throughput for CNN workloads by leveraging a spatial
architecture with a 2D mesh of processing elements.
Cerebras Wafer-Scale Engine (WSE): Cerebras Systems has developed the
Wafer-Scale Engine, which is a massive systolic array processor fabricated
on a single wafer. This architecture enables highly parallel computation for
large-scale neural networks and other AI workloads, leveraging the
massive on-chip interconnect bandwidth provided by the systolic array
design.

38. 1. YOUTUBE: https://youtu.be/8zbh4gWGa7I?si=rhC0xGlJ0V3RGpQ3
https://youtu.be/vADVh1ogNo0?si=nbmOCHmfdXwF8_GT
https://youtu.be/cmy7LBaWuZ8?si=6QEZQ2UaOHxsCK4r
2. Computer Architecture by Kai Hwang Kai Hwang & F. A. Briggs,
“Computer Architecture and Parallel Processing”, McGraw Hill