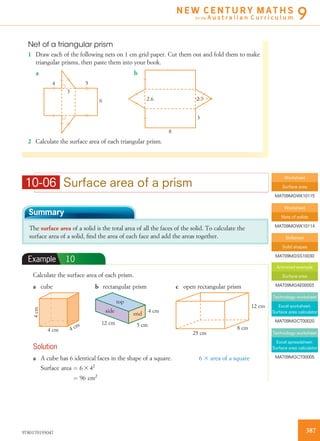
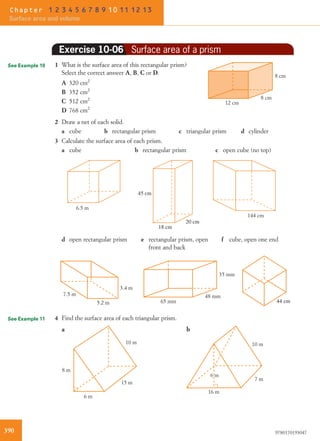
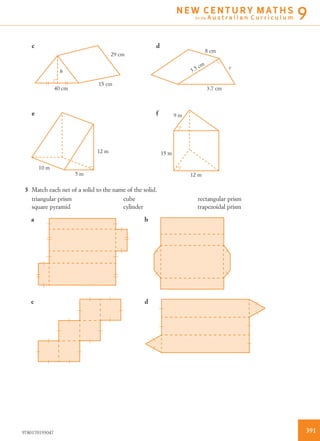
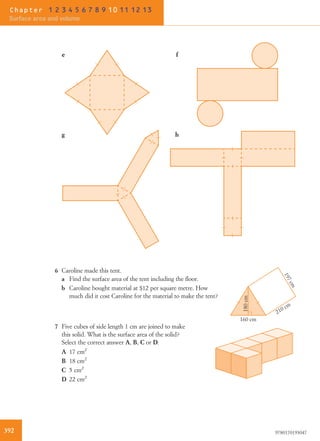
The Sydney Opera House was designed by Danish architect Jørn Utzon between 1955 and 1973. Its distinctive shell design represents a ship under full sail, with each concrete shell being a segment of a sphere with a radius of 75.2 meters. The shells are covered with over 1 million white and cream tiles. The Sydney Opera House sits on 1.3 hectares of land and is 183 meters long and 120 meters wide at its widest point.