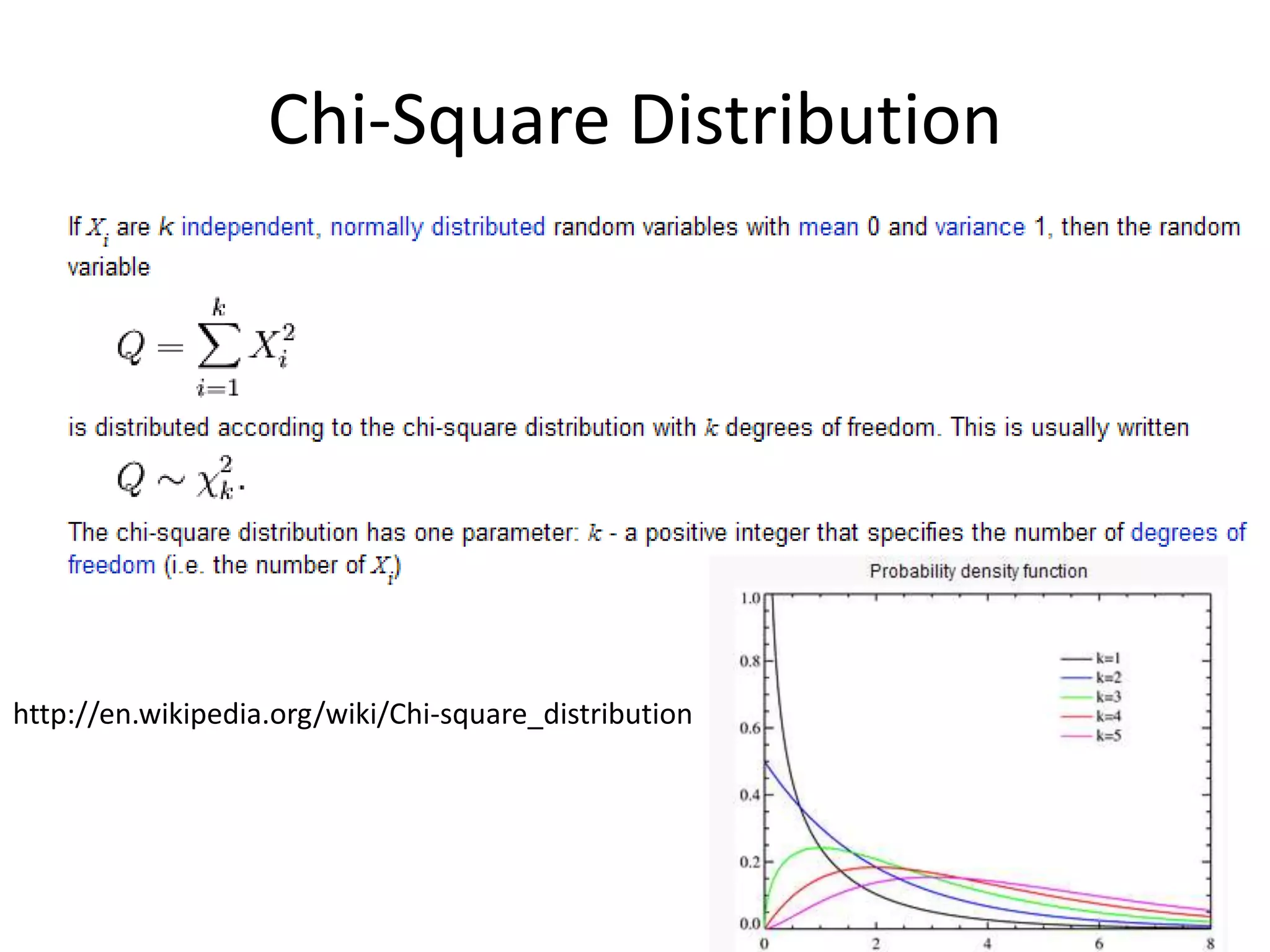
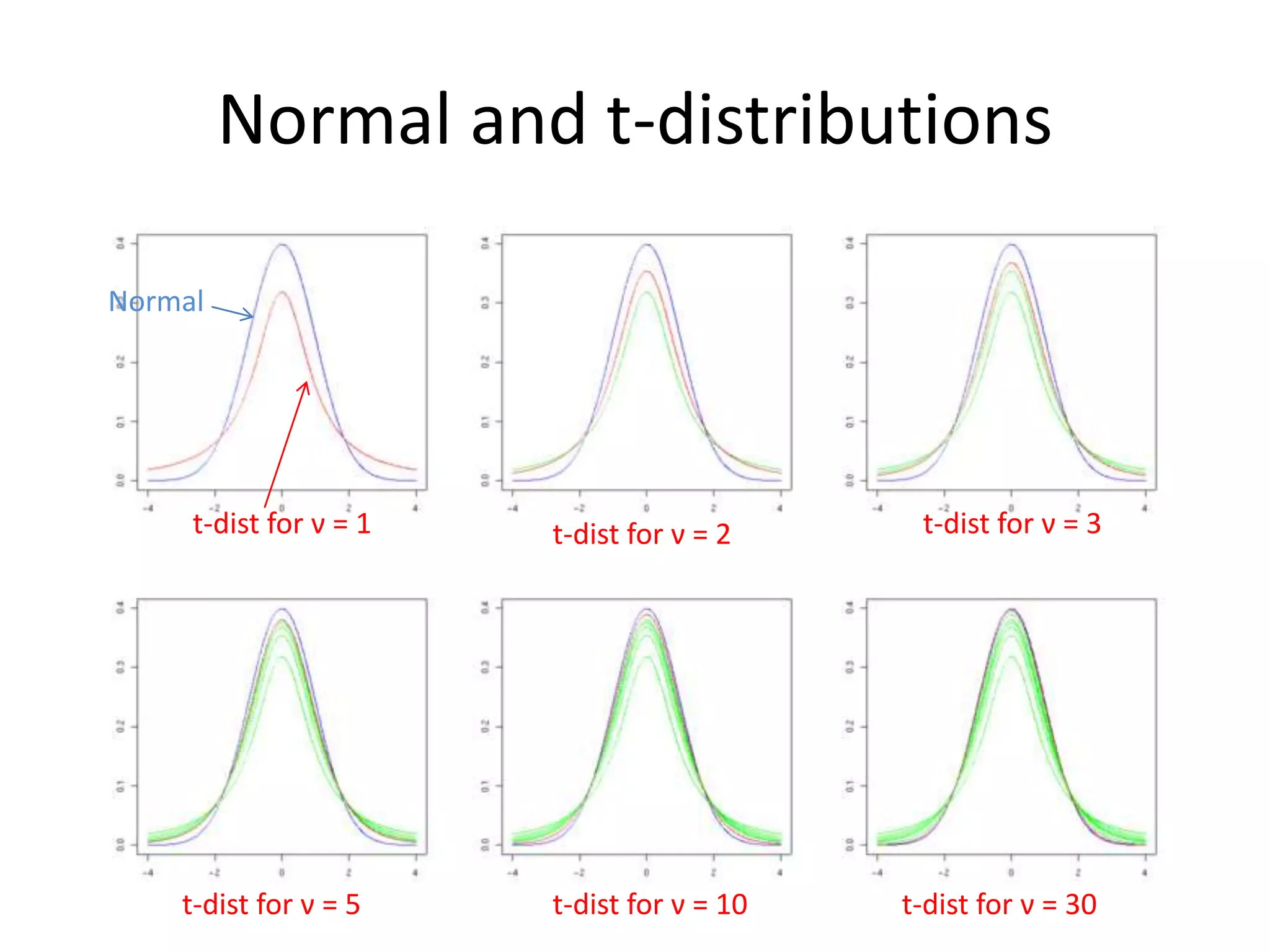
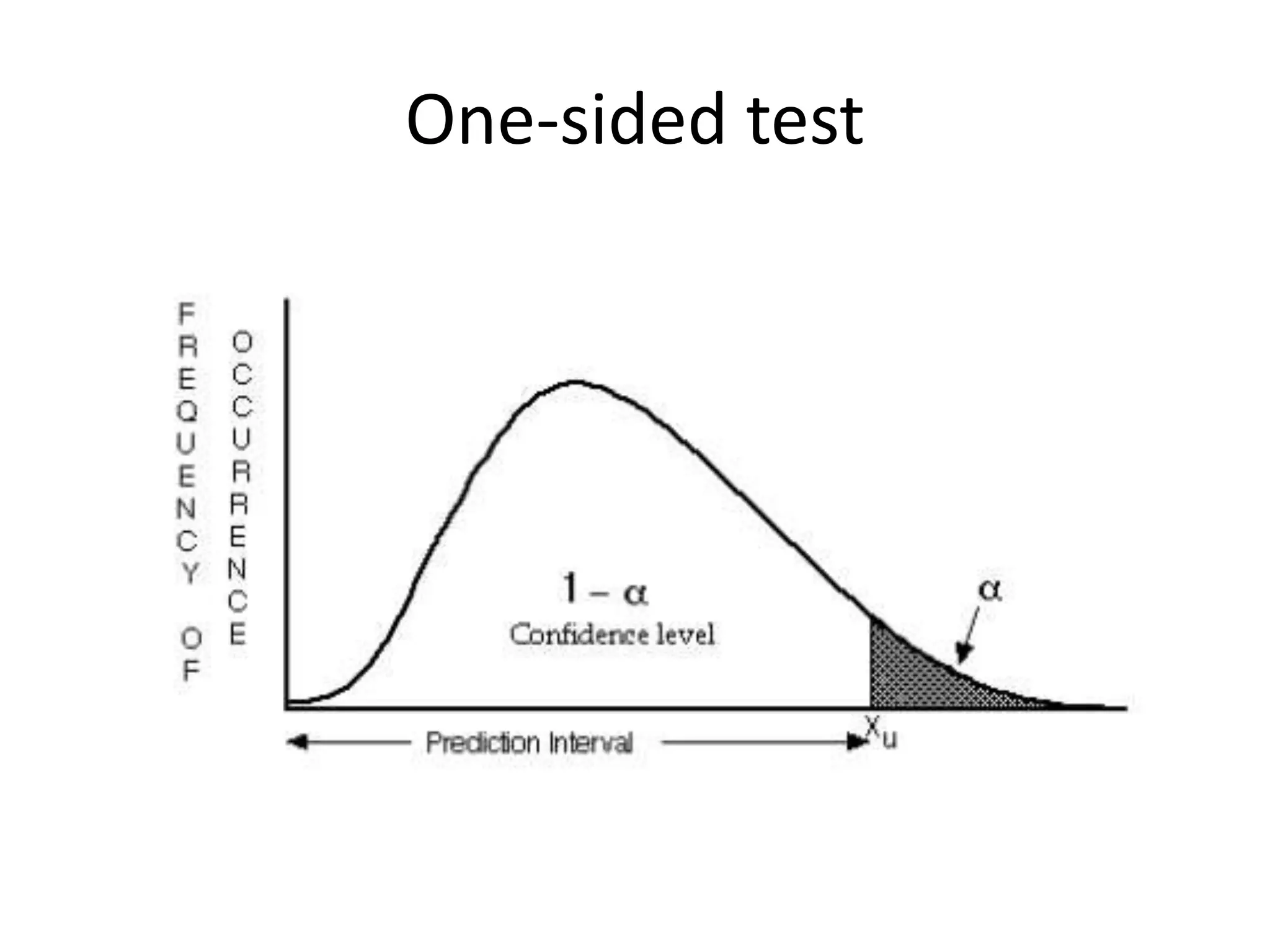
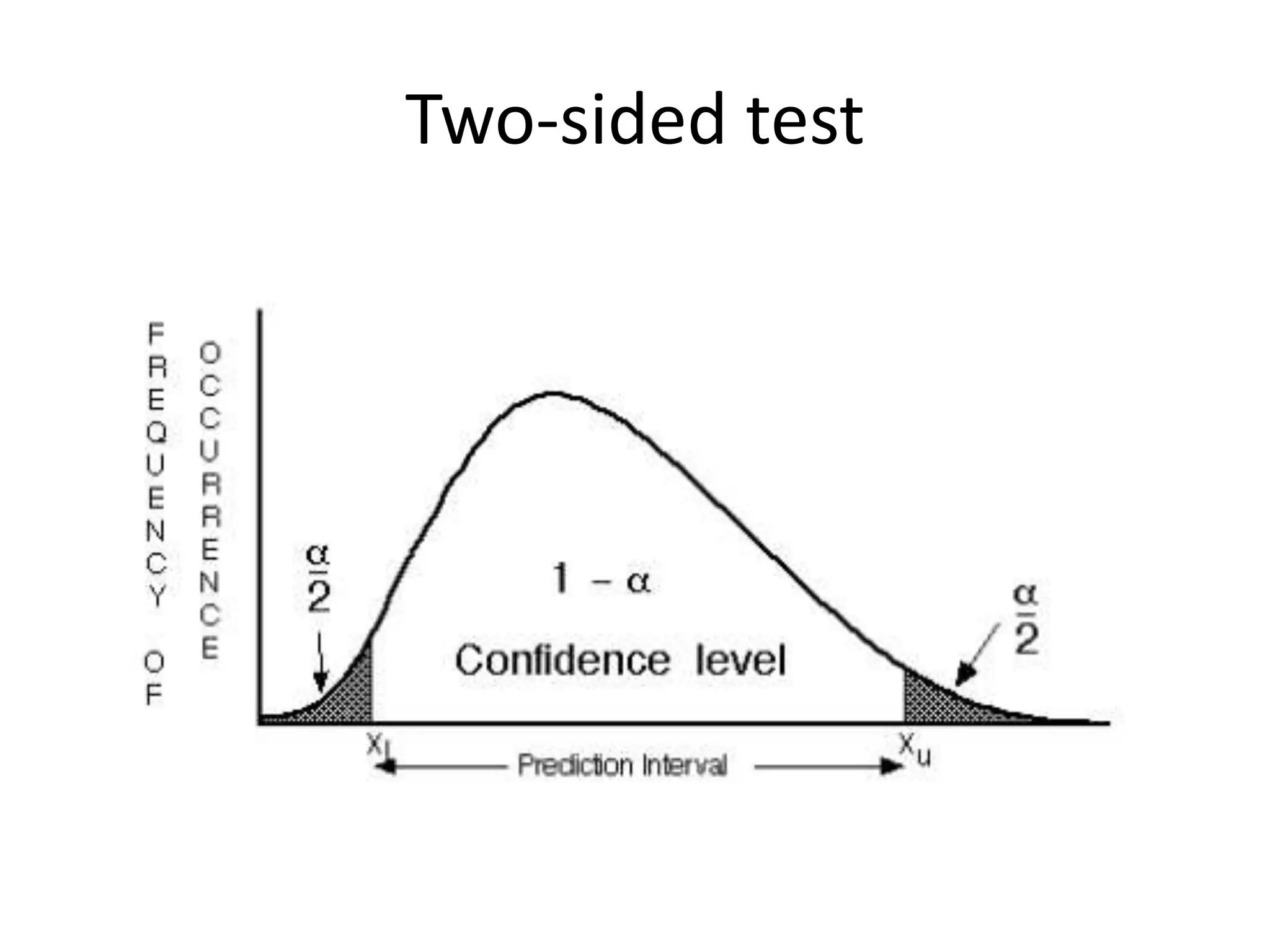
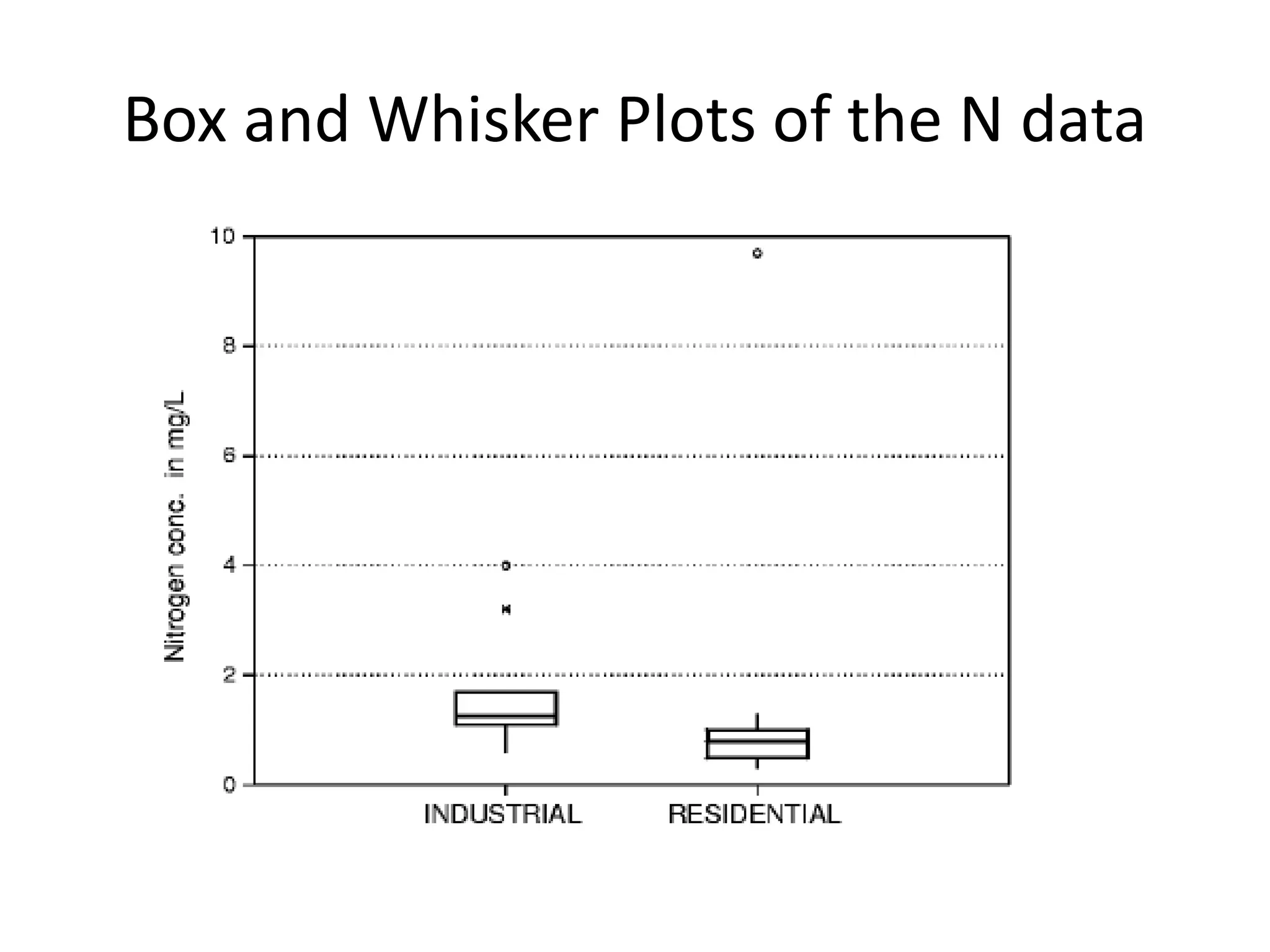
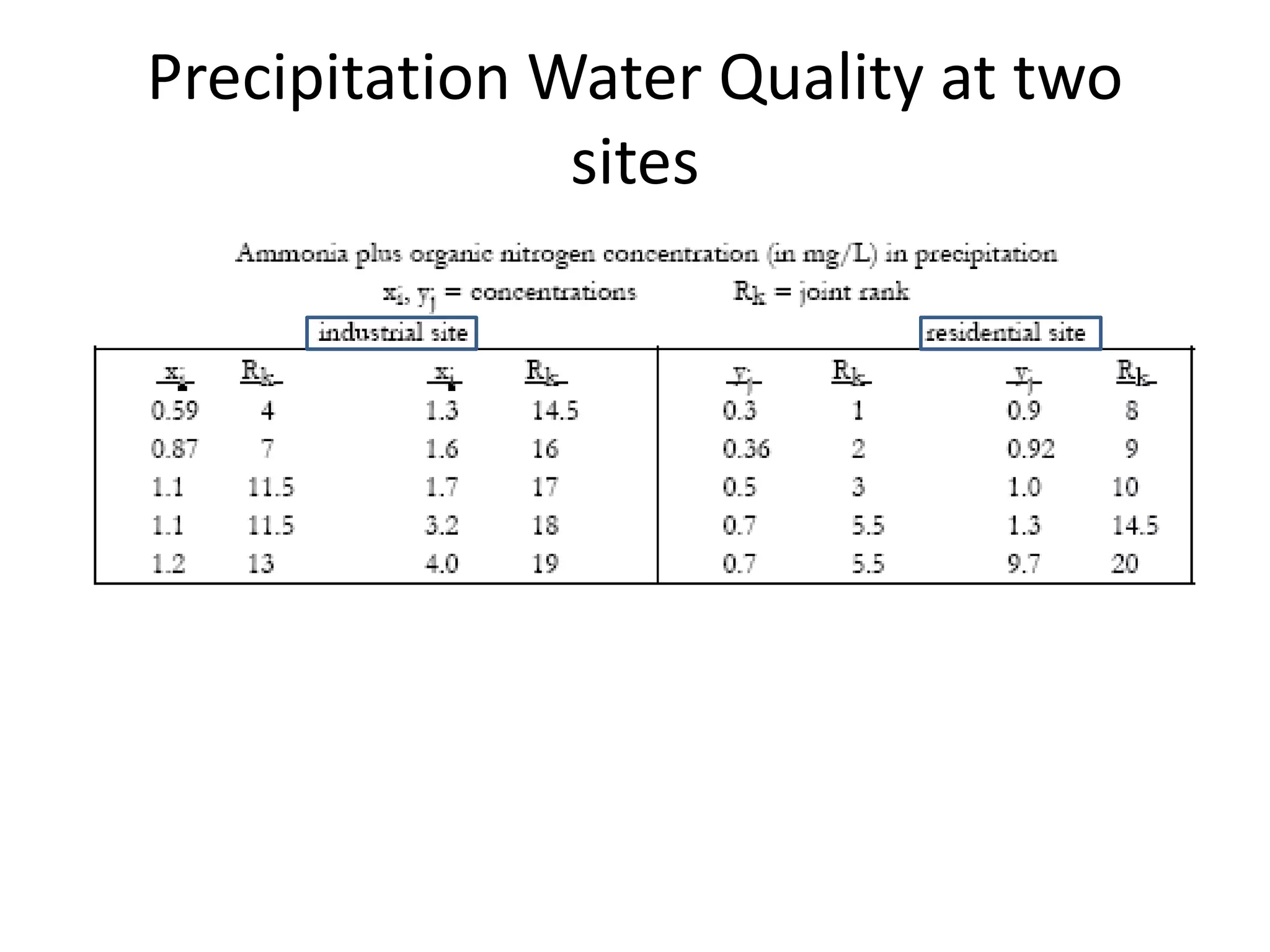
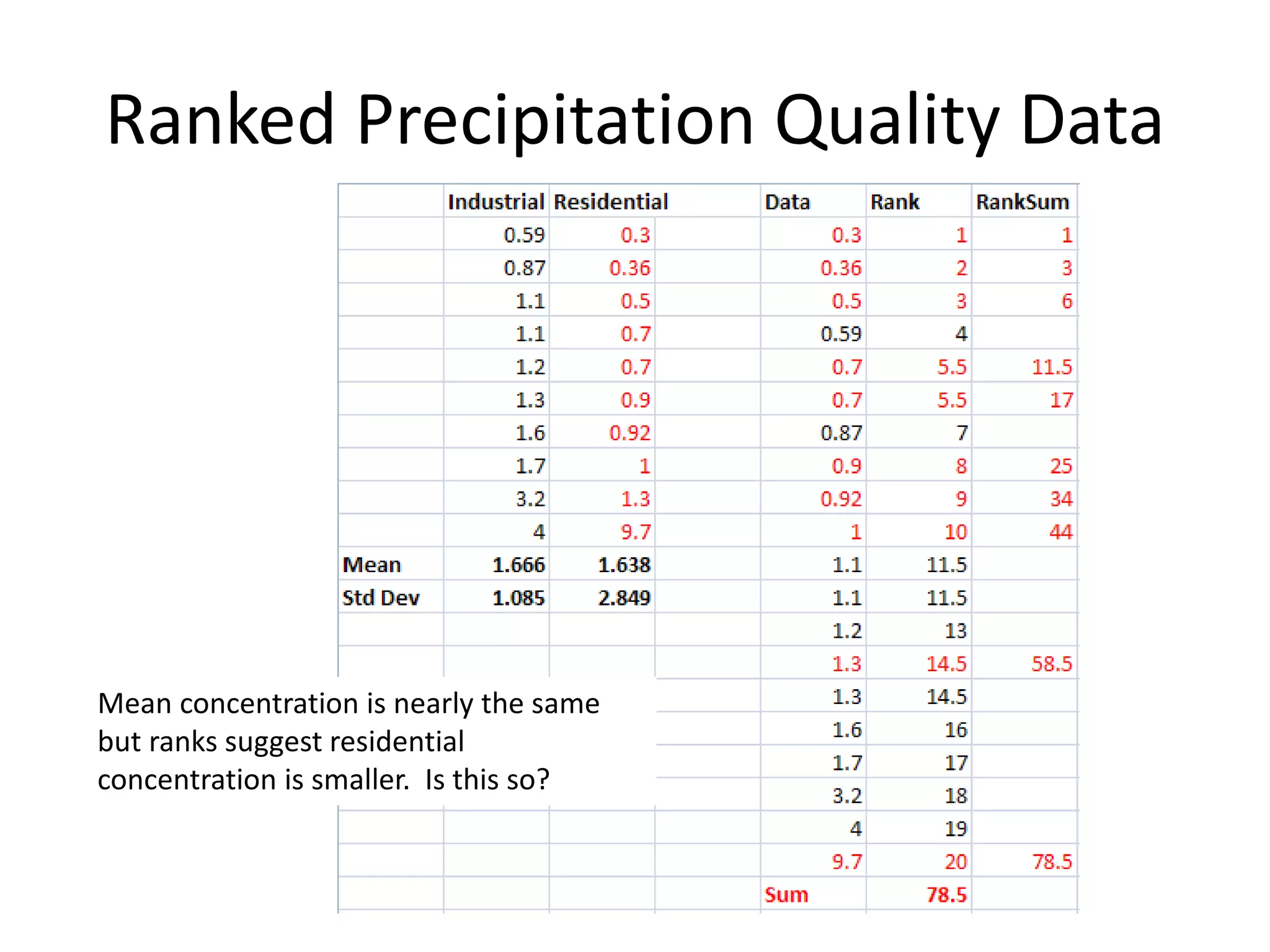
This document discusses statistical techniques for comparing two sets of data, including the t-distribution for unknown standard deviations, hypothesis testing, and the Wilcoxon rank-sum test. It provides examples of using the Wilcoxon rank-sum test to compare precipitation water quality data from two sites and determine that the residential concentration is lower than the industrial concentration with a p-value of 0.024.

1. Statistics in Water Resources, Lecture 6
• Key theme
– T-distribution for distributions where standard
deviation is unknown
– Hypothesis testing
– Comparing two sets of data to see if they are
different
• Reading: Helsel and Hirsch, Chapter 6
Matched Pair Tests

2. Chi-Square Distribution
http://en.wikipedia.org/wiki/Chi-square_distribution

3. t-, z and ChiSquare
Source: http://en.wikipedia.org/wiki/Student's_t-distribution

4. Normal and t-distributions
Normal
t-dist for ν = 1
t-dist for ν = 30
t-dist for ν = 5
t-dist for ν = 3
t-dist for ν = 2
t-dist for ν = 10

5. • Standard Normal z
– X1, … , Xn are
independently
distributed (μ,σ), and
– then
is normally distributed with
mean 0 and std dev 1
Standard Normal and Student - t
• Student’s t-distribution
– Applies to the case
where the true standard
deviation σ is unknown
and is replaced by its
sample estimate Sn

6. 6
p-value is the probability of obtaining the value of the
test-statistic if the null hypothesis (Ho) is true
If p-value is very small (<0.05 or 0.025) then reject Ho
If p-value is larger than α then do not reject Ho

7. One-sided test

8. Two-sided test

9. Helsel and Hirsch p.120

10. Box and Whisker Plots of the N data

11. Precipitation Water Quality at two
sites

12. Ranked Precipitation Quality Data
Mean concentration is nearly the same
but ranks suggest residential
concentration is smaller. Is this so?

13. Wilcoxon Rank Sum Test
Helsel and Hirsch p. 462
This is < 0.05 for a one-sided test,
thus reject Ho and say residential
concentration is lower than
industrial
p-value in middle is for P(Wrs > X)
or P(Wrs < X*) for m = n = 10
Note that the sum of n = 1, 2, ….
20 = 210 and X + X* = 210 in all
cases in this table.
Test sum
of higher
ranks
Test sum
of lower
ranks
p-value is 0.024 for
Rank sum of 78.5