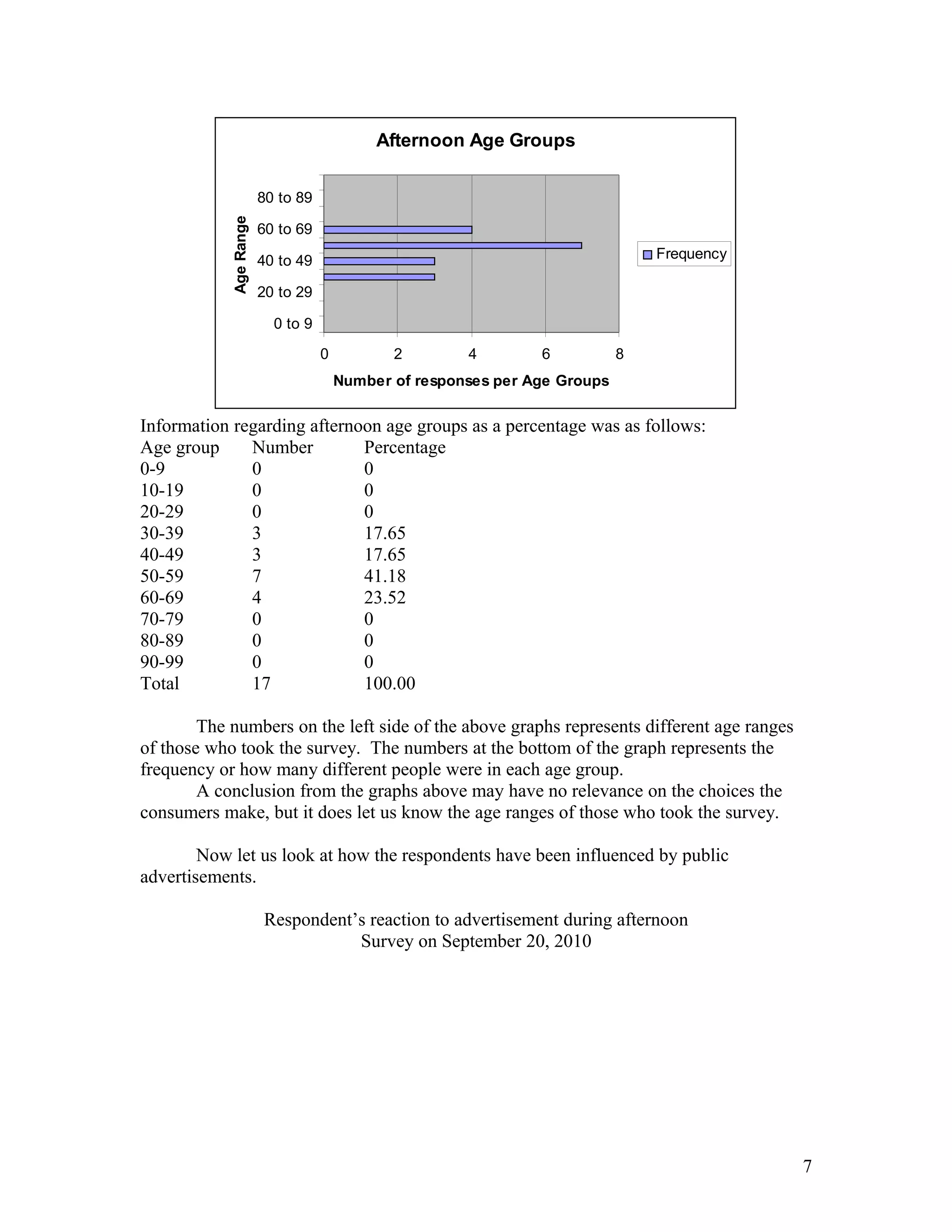
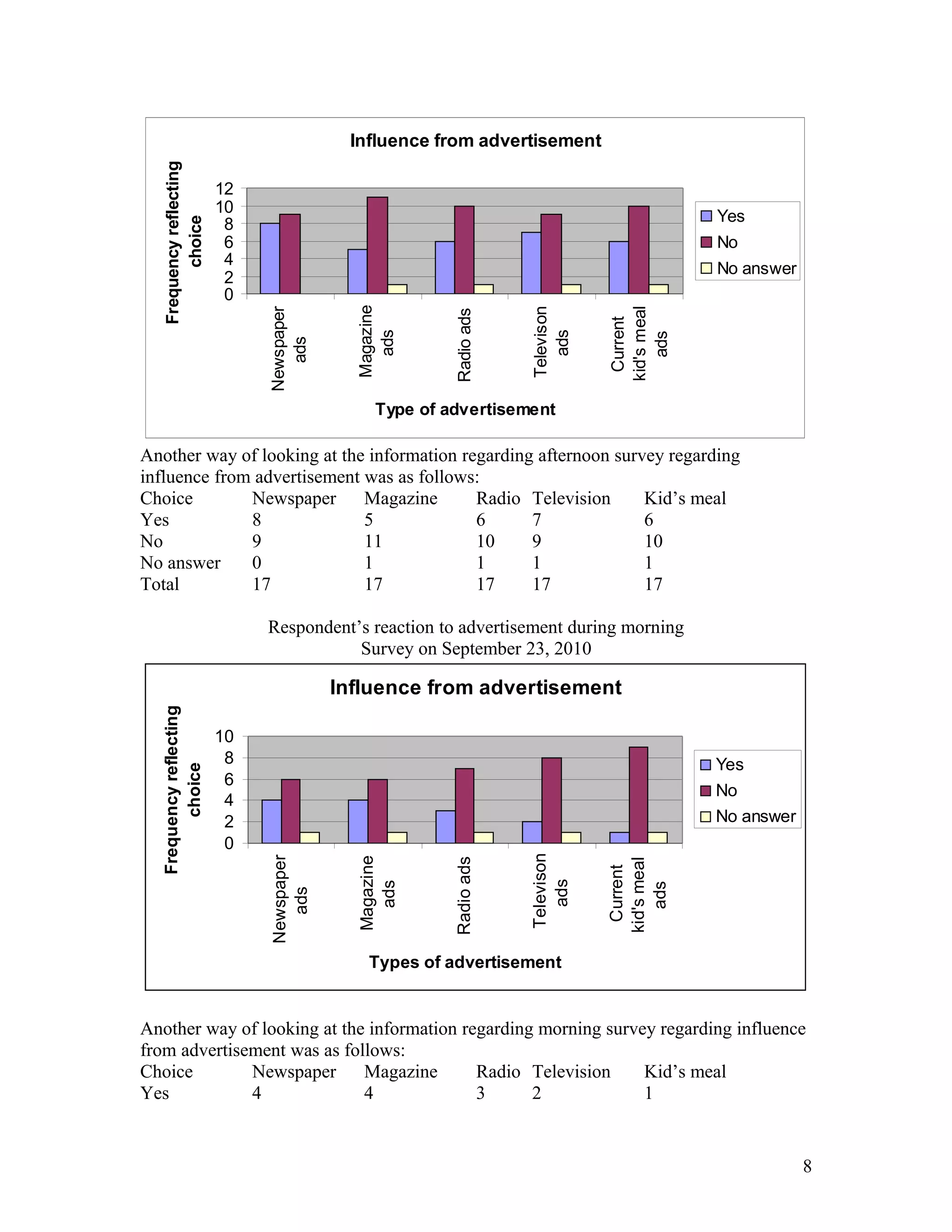
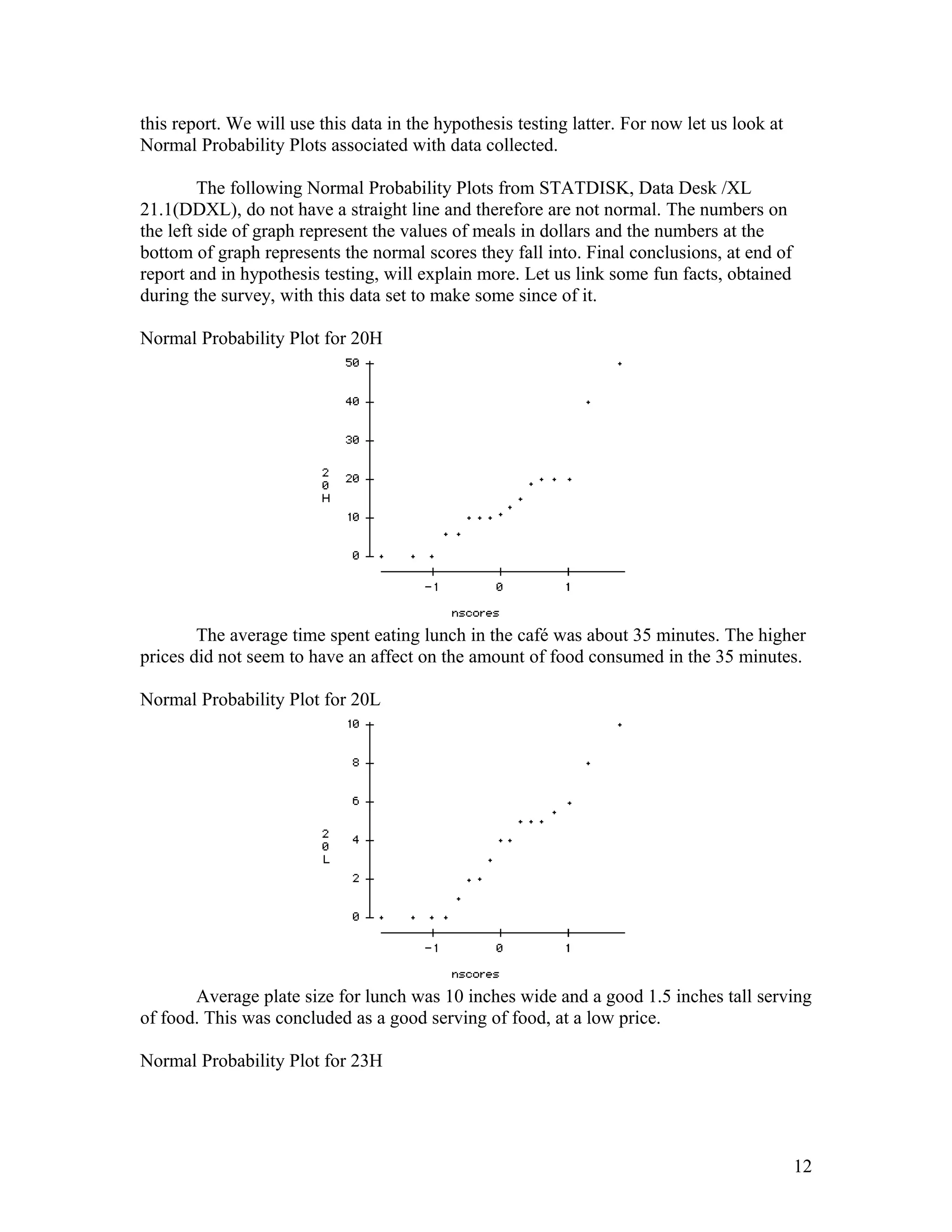
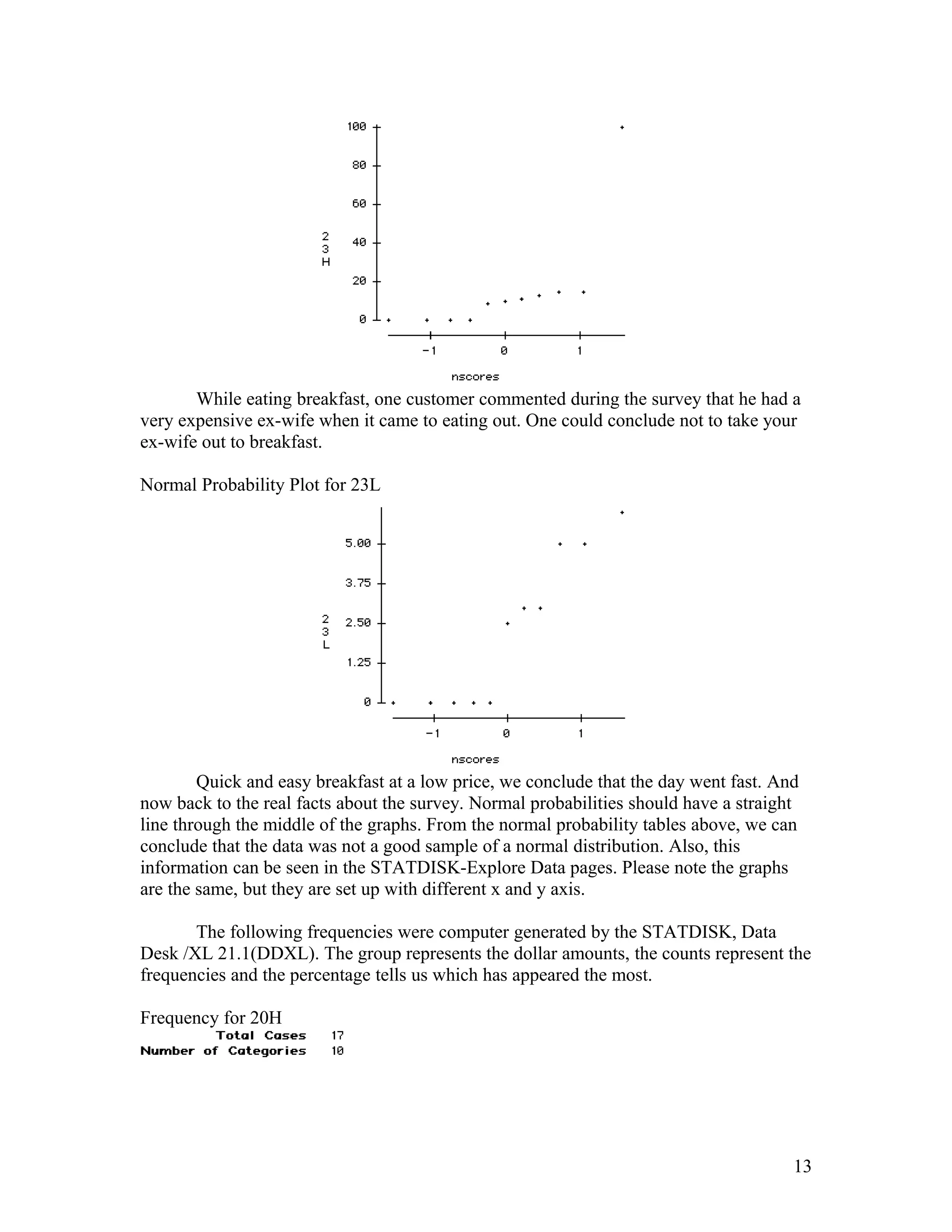
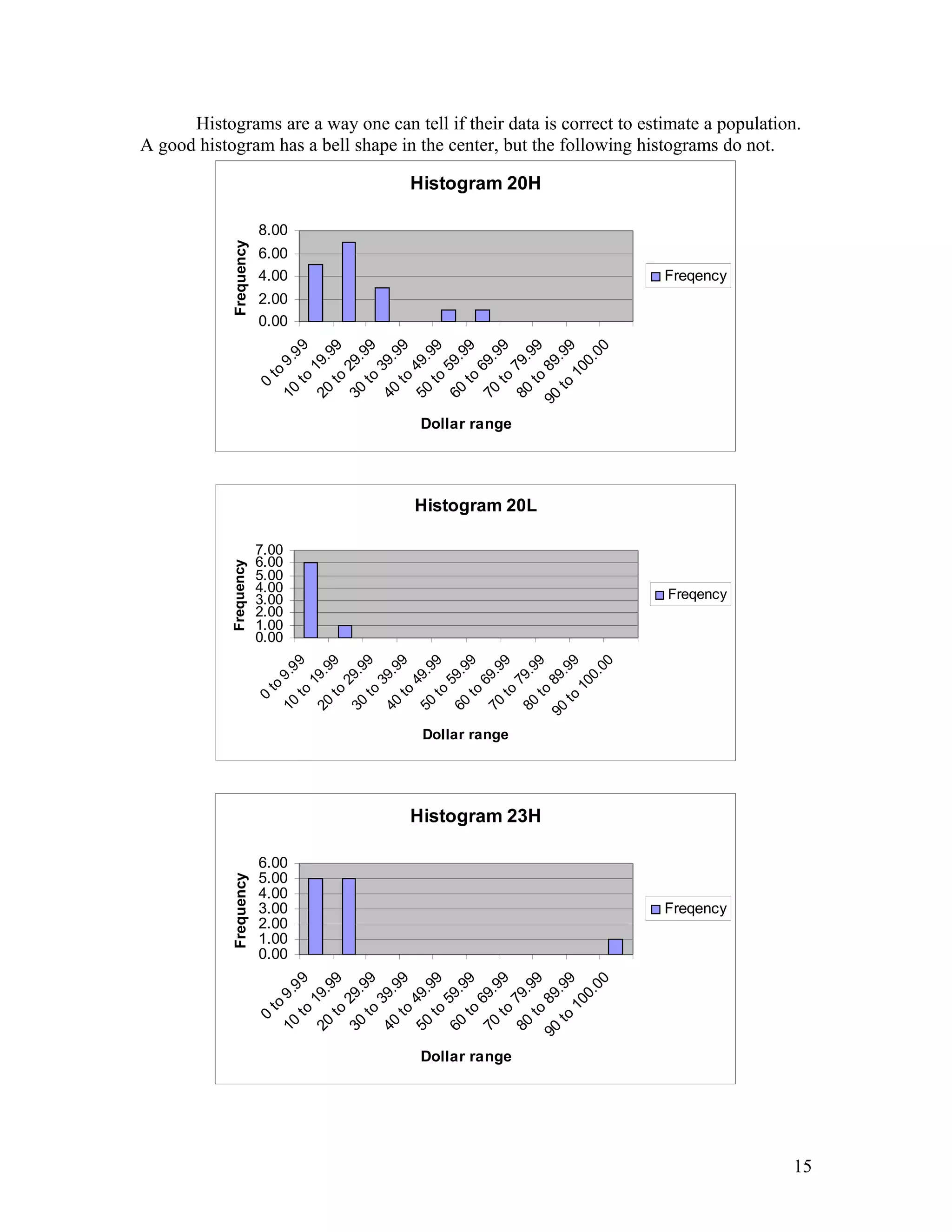
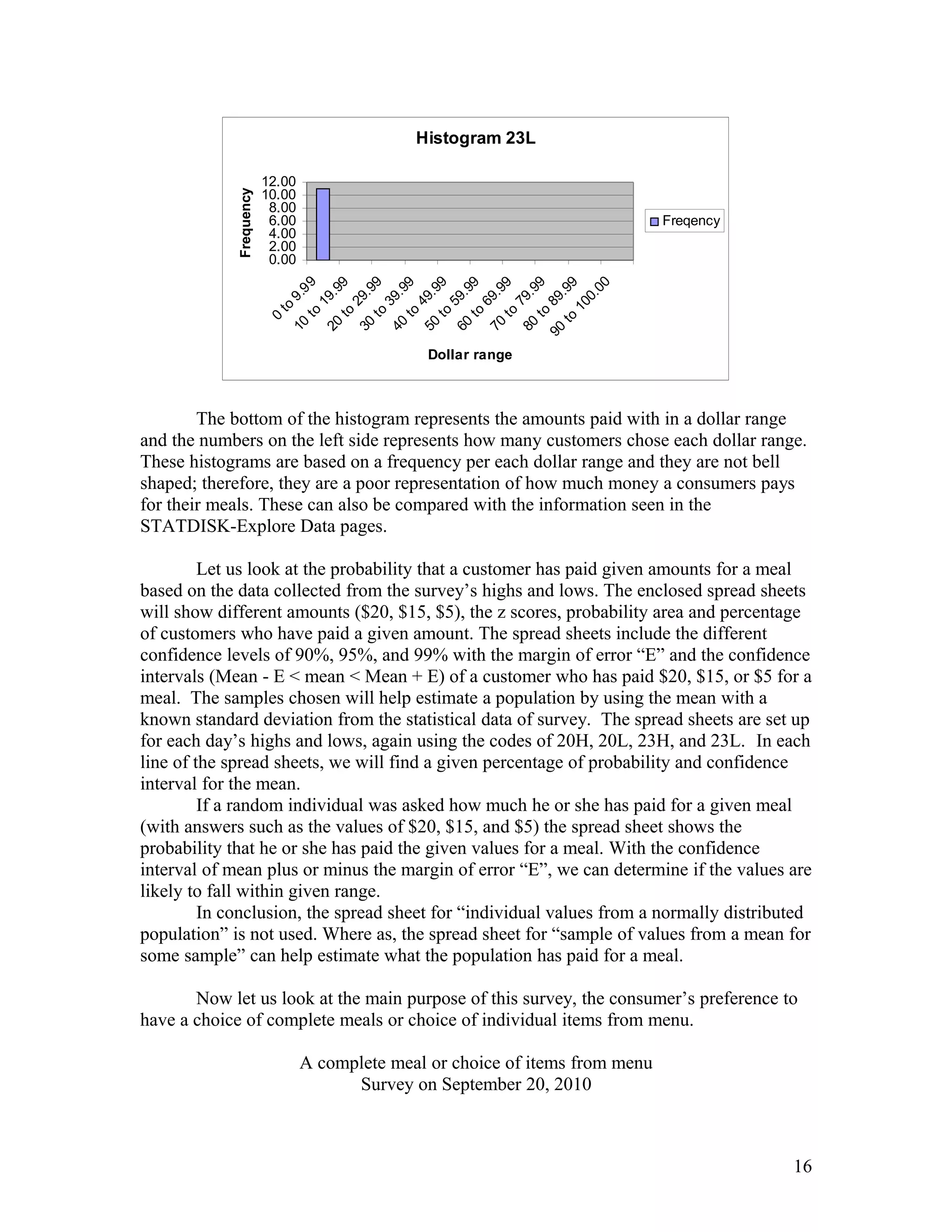
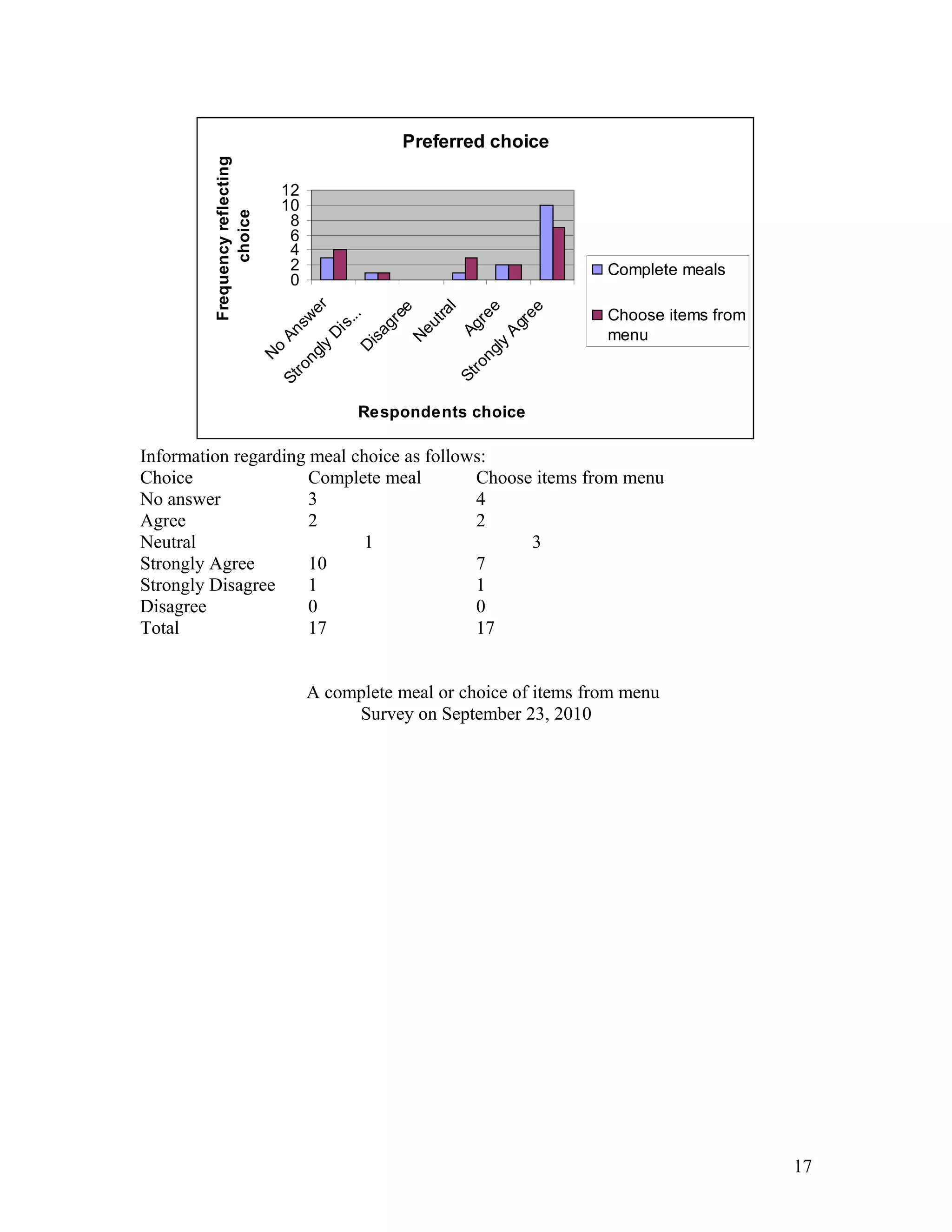
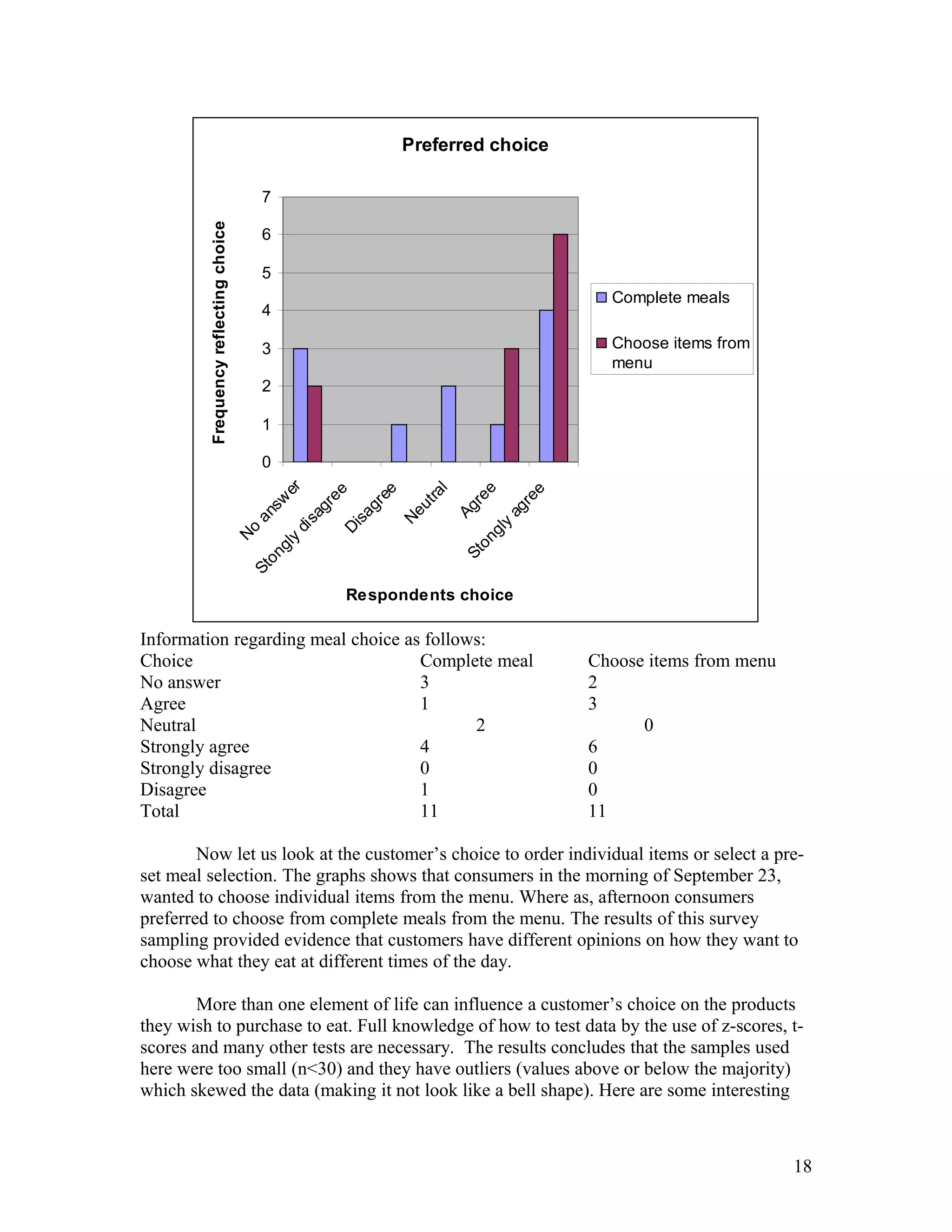
- Ellen Wells conducted a survey of customers at B&J's Café to study their preferences for complete meals or individual menu items. - She surveyed customers over two days, collecting data on age, influences on their choices, and prices paid for meals. - Ellen analyzed the data using statistical tests and found evidence that individual items are typically priced under $15, while there was no evidence that complete meals are usually priced over $15. This supports the hypothesis that customers prefer choosing individual menu items.

1. Ellen Wells
Professor Bryan
Statistics
December 9, 2010
Description of Project
The study compares slow cook orders for different times during the day, such as
morning and afternoon.
The project was designed to look at the consumer’s ages by groups, what
influences them when they look at advertisements, the prices they have paid for a meal,
and the key issue is to determine if customers would prefer complete meals from menus
or their choice of individual items.
This was a self selected subject by me, Ellen Wells. I have been interested in this
topic, because I have observed customers who cannot decide which foods they want to
order from a menu.
How will you study the project?
The project was studied by the use of a survey I created. In regards to B & J’s
Café, on day one, I walked into the café and asked the owner, Mrs. Huckaby, if I could
survey her customers. She was accepting to the idea of the survey. I told her that I had a
rough draft of possible data, but I did not know enough about the project at the given
moment. I needed to get more information about the project from the instructor. I
explained that I would be working on a formal letter of request to survey her cafe and
would be back at a future date. On the second day, I took the formal letter and a copy of
the survey to the café. I told the owner that I would check with her in a few days. On the
third day, I asked again if I may do my survey and it was approved. I asked if one day in
the coming week would be acceptable to begin the survey and received a yes. At end of
first survey execution, I thanked the owner and requested another day to survey the
customers. In a few days, I was back to do the second survey. At the end of the day, I told
the owner that the project would not be completed until December.
To collect the data on the survey execution days, I waited near the exit and near
the cashier’s check out for customers to pay for their meals. As the bill was being totaled,
I asked if they would help a college student with a statistic’s survey project. Please see
survey sample and letters of request at end of report.
The first survey was conducted by me, Ellen Wells at B & J’s Café 8155 Lander
Avenue, Hilmar, CA 95324, on September 20, 2010 from 11:00am to 1:45pm. The
second survey was conducted by me, Ellen Wells at B & J’s Café 8155 Lander Avenue,
Hilmar, CA 95324, on September 23, 2010 from 7:00am to 9:45am.
I am interested in this topic, because I have observed customers who cannot
decide which foods they want from the menu.
1

2. Collection of data
Tables of raw data that can be found at the end of the report are as follows:
1. Copies of survey and letters of request.
2. Raw data collected from customer survey.
3. Full original data in Microsoft excel spread sheet, one collection of pages for the
morning survey and one collection of pages for the afternoon survey.
4. Parts of Microsoft excel spread sheet data and graphs to help explain who the
respondents are by their age groups.
5. Parts of Microsoft excel spread sheet data and graphs to help explain respondent’s
choices through the influence of advertisement.
6. Parts of Microsoft excel spread sheet data and graphs with STATDISK-Explore
Data to help understand consumer’s choice in regards to price of a meal.
7. Parts of Microsoft excel spread sheet data and graphs to help explain customer’s
preference when choosing items from the menu.
8. Excel spread sheets used for Z-scores, Probabilities, Confidence Intervals, P-
values, and Hypothesis testing.
9. Vocabulary for box plot data from STATDISK.
10. Follow up letter and thank you to B & J’s Café.
Hypothesis test
Now we will look at the hypothesis test. The initial hypothesis will support, fail to
support, confirm, or fail to confirm initial hypothesis of the project. It was expected that
most customers would prefer to choose individual items from a menu. In general, higher
prices paid for a meal at a café represent a complete meal and lower prices paid represent
smaller more affordable individual items.
It is important to use a hypothesis test that is appropriate for your data. For
example, my values for the price of a meal are to be from a normal distribution. Since the
café population is considered normal, any size sample will be normally distributed. This
allows the use of the Central Limit Theorem as shown in the corresponding spread sheet
and steps for hypothesis test. Therefore, I will use a hypothesis test that looks at “Test
statistic for mean” and provides a Z-score. A z-score measures the number of standard
deviations from the mean (a particular data point or a measure of center). Please see
spread sheet titled “Hypothesis Test with Z score” at end of report. The information on
the spread sheet is expressed in the five steps below.
We will pretend that the data collected has a bell shape and it is normally
distribute. This will allow the use of the z-score test for hypothesis. The other option is a
t-score test that has a shorter height to the top of the bell shape and a wider ends from the
center of the bell shape. I would prefer to look at a more precise data set provided by the
z-score.
Step 1
The statistical conclusion: the claim is that most customers would prefer to choose
individual items from a menu based on the prices they have paid. In general, the higher
2

3. prices paid for a meal at a café represents a complete meal and lower prices paid
represents individual items for a meal.
Therefore, individual items are expected to be less than $15.00 and complete
meals are expected to be more than $15.00.
Claims: individual items are expected to be less than $15.00 and complete meals are
expected to be more than $15.00.
20L Individual items for lunch µ < $15.00
Null hypothesis H0: µ ≥ $15.00 Alternative hypothesis H1: µ < $15.00
20H Complete meals for lunch µ > $15.00
Null hypothesis H0: µ ≤ $15.00 Alternative hypothesis H1: µ > $15.00
23L Individual items for breakfast µ< $15.00
Null hypothesis H0: µ ≥ $15.00 Alternative hypothesis H1: µ < $15.00
23H Complete meals for breakfast µ > $15.00
Null hypothesis H0: µ ≤ $15.00 Alternative hypothesis H1: µ > $15.00
Step 2
Level of significance: α = .05
Step 3
Test statistic: Z-score =
x-µ
σ/ √n
Requirements: Large sample or small sample with normal distribution, also
1) The sample is a simple random sample
2) The value of the population standard deviation σ is known
3) Either or both of these conditions is satisfied: The population is normally
distributed or n > 30
In n ≤ 30, we can consider the normality requirement to be satisfied if there are no
outliers and if a histogram of the sample data has a perfect bell shape.
Step 4
State the decision Rules: If p-value ≤ α reject H0 & If p-value > α fail to reject H0
Written decision rule: If α = .05 and is ≥ P-value, then reject H0
Step 5
Do calculations:
3

4. Please note the set up for the calculation: z-score equals the “mean” from the survey data
less the “claim” divided by modified standard deviation used in the Central Limit
Theorem.
Recall:
20L Individual items for lunch µ < $15.00
Null hypothesis H0: µ ≥ $15.00 Alternative hypothesis H1: µ < $15.00
Calculate:
20L Individual items for lunch µ < $15.00
3.557647-15 = -15.59
2.957234/ √17
P (Z > -15.59) = 0.0001
P-value = 1-area =0.0001 (one tailed test)
Since H0 has ≥ we use a one tail test
So 0.0001 < α which is 0.05, reject H0
Conclusion: There is sufficient evidence to support the claim that individual items are
expected to be less than $15.00.
Recall:
20H Complete meals for lunch µ > $15.00
Null hypothesis H0: µ ≤ $15.00 Alternative hypothesis H1: µ > $15.00
Calculate:
20H Complete meals for lunch µ > $15.00
14.70471-15 = -0.09
13.39667/ √17
P (Z > -0.09) = 0.4641
P-value = 1-area = 0.4641 (one tailed test)
Since H0 has ≥ we use a one tail test
So 0.4641 > α which is 0.05, fail to reject H0
Conclusion: There is not sufficient evidence to support the claim that complete meals are
expected to be more than $15.00.
Recall:
23L Individual items for breakfast µ< $15.00
Null hypothesis H0: µ ≥ $15.00 Alternative hypothesis H1: µ < $15.00
Calculate:
23L Individual items for breakfast µ< $15.00
2.225455-15 = -17.95
2.359048/ √11
P (Z > -17.95) = 0.0001
P-value = 1-area = 0.0001 (one tailed test)
Since H0 has ≥ we use a one tail test
So 0.0001 < α which is 0.05, reject H0
4

5. Conclusion: There is sufficient evidence to support the claim that individual items are
expected to be less than $15.00.
Recall:
23H Complete meals for breakfast µ > $15.00
Null hypothesis H0: µ ≤ $15.00 Alternative hypothesis H1: µ > $15.00
Calculate:
23H Complete meals for breakfast µ > $15.00
15.72727-15 = 0.08
28.63596/ √11
P (Z > 0.08) = 0.4681
P-value = 1-area = 0.4681 (one tailed test)
Since H0 has ≥ we use a one tail test
So 0.4681 > α which is 0.05, fail to reject H0
Conclusion: There is not sufficient evidence to support the claim that complete meals are
expected to be more than $15.00.
Reporting of Results
The items a consumer chooses, reflects a person’s choice of how they wish to
order food from a menu. Observation of consumers has shown that consumers have
trouble in selecting items from a menu. A survey was conducted by, me, Ellen Wells; a
student from Merced Community College, for a class project to help better understand
statistics and the choices of consumers. The survey’s purpose was the consumer’s
preference to have a choice of complete meals or choice of individual items from menu.
Since this was based on a non numerical selection, let us look at the highest and lowest
paid amounts for a meal and how the price influences choice. The prices have helped us
determine the customer’s choice of complete meals or individual items from the menu.
The survey, given to the consumers, was large and covered many topics. Only a few will
be explained in this report.
To understand the survey, I looked at some simple information about the
respondents. The respondents who completed the survey consist of various age ranges.
They were in Hilmar, California, a small town. The approximated number of customers
who did not take survey, but were in the store (on September 23, 2010 in the morning)
was eleven and (on September 20, 2010 in the afternoon) was thirty.
Let us focus on those who completed the survey. Those who completed the survey
on September 23, 2010 amounted to eleven respondents and on September 20, 2010
amounted to seventeen respondents.
The statistical data collected has been used to obtain inferential statistics about a
normally distributed population. A small sample of customers will provide information
about the entire population that visit the café.
The technologies used to help understand the statistical data are as follows: 1)
Microsoft Excel 2003, 2) STATDISK computer software called Data Desk /XL
21.1(DDXL) from Elementary Statistics, 11th
ed., by Mario F. Triola, and 3) STATDISK
computer software called Statdisk 11.0.0 from Elementary Statistics, 11th
ed., by Mario F.
Triola.
5

6. Please note the special structure of the following information, first, a brief
statement of topic; second, graphical presentations of data collected; and third, an
explanation with conclusion drawn regarding findings.
The respondents have been broken into age groups to help better understand those
who took the survey.
Respondents by age group during morning
Survey on September 23, 2010
Morning Age Groups
0 2 4 6
0 to 9
20 to 29
40 to 49
60 to 69
80 to 89
AgeRange
Number of responses per Age Groups
Frequency
Information regarding morning age groups as a percentage was as follows:
Age group Number Percentage
0-9 0 0
10-19 0 0
20-29 0 0
30-39 1 9.09
40-49 1 9.09
50-59 5 45.45
60-69 1 9.09
70-79 3 27.27
80-89 0 0
90-99 0 0
Total 11 99.99
Rounding miscalculation reflected in the 99.99 percent which is 100 percent.
Respondents by age group during afternoon
Survey on September 20, 2010
6

7. Afternoon Age Groups
0 2 4 6 8
0 to 9
20 to 29
40 to 49
60 to 69
80 to 89
AgeRange
Number of responses per Age Groups
Frequency
Information regarding afternoon age groups as a percentage was as follows:
Age group Number Percentage
0-9 0 0
10-19 0 0
20-29 0 0
30-39 3 17.65
40-49 3 17.65
50-59 7 41.18
60-69 4 23.52
70-79 0 0
80-89 0 0
90-99 0 0
Total 17 100.00
The numbers on the left side of the above graphs represents different age ranges
of those who took the survey. The numbers at the bottom of the graph represents the
frequency or how many different people were in each age group.
A conclusion from the graphs above may have no relevance on the choices the
consumers make, but it does let us know the age ranges of those who took the survey.
Now let us look at how the respondents have been influenced by public
advertisements.
Respondent’s reaction to advertisement during afternoon
Survey on September 20, 2010
7

8. Influence from advertisement
0
2
4
6
8
10
12
Newspaper
ads
Magazine
ads
Radioads
Televison
ads
Current
kid'smeal
ads
Type of advertisement
Frequencyreflecting
choice
Yes
No
No answer
Another way of looking at the information regarding afternoon survey regarding
influence from advertisement was as follows:
Choice Newspaper Magazine Radio Television Kid’s meal
Yes 8 5 6 7 6
No 9 11 10 9 10
No answer 0 1 1 1 1
Total 17 17 17 17 17
Respondent’s reaction to advertisement during morning
Survey on September 23, 2010
Influence from advertisement
0
2
4
6
8
10
Newspaper
ads
Magazine
ads
Radioads
Televison
ads
Current
kid'smeal
ads
Types of advertisement
Frequencyreflecting
choice
Yes
No
No answer
Another way of looking at the information regarding morning survey regarding influence
from advertisement was as follows:
Choice Newspaper Magazine Radio Television Kid’s meal
Yes 4 4 3 2 1
8

9. No 6 6 7 8 9
No answer 1 1 1 1 1
Total 11 11 11 11 11
The numbers on the left side of the graph represents how many different people
chose a particular medium of advertisement. The advertisement medium is listed on the
bottom of the graph.
Notice on September 20, 2010 the most chosen media for “no” influence by
advertisement was the magazine ads. Where as, the most chosen media for “yes”
influence was the newspaper ads. On September 23, 2010, the most chosen media for
“no” influence by advertisement was the current kid’s meal ads. Where as, the most
chosen media for “yes” influence was a tie between the newspaper ads and magazine ads.
The survey shows the consumers are not influenced by public advertisement. One could
conclude that advertisement has only a minimal role in how consumers have chose their
meals due to consumer’s choices of “no” influence being the leading selection in both
surveyed days. One could conclude that prices in the advertisement offers do not have an
influence over the choice of items from a menu, but let’s look at the prices from the
menu.
One thing that may make choosing items from a menu difficult is the price. Let us
look at a comparison of highest paid amounts and lowest paid amounts for a meal in
regards to the two different days surveyed (September 20 and 23). By examining the
prices paid we can learn how to predict what customers will pay in the future. The
following tables can help us understand where the middle value and willingness to pay
for meals lies within data collected.
Before we look at the data, let us understand the labeling of the survey data as
follows:
20H is the data set for highest paid amounts collected on September 20, 2010.
23H is the data set for highest paid amounts collected on September 23, 2010.
20L is the data set for lowest paid amounts collected on September 20, 2010.
23L is the data set for lowest paid amounts collected on September 23, 2010.
I have stepped out side the box and used technology to do something it was not
intended to do. A contingency table is a table in which frequencies correspond to two
variables (one variable used to categorize rows and a second variable is used to
categorize columns). I manipulated the computer system to show the true values of my
survey. By reading the right totaled column and the bottom totaled column, we can
determine which amounts paid were the most popular or the amount customers were most
willing to pay.
Contingency tables for September 20th:
9

10. The above table concludes that customers have paid between $5.00 and $20.00 for
their lunch meals. Observation of customer’s meals during this survey revealed that about
twenty five percent ordered breakfast for lunch.
Contingency tables for September 23th:
The above table shows that customers have paid between $5.00 and $15.00 for
their breakfast meals.
10

11. A box plot can help us understand how prices have had an influence on choices
made for a meal. The survey has asked the consumers to fill in the highest and lowest
amount paid for a meal.
Box Plot Data from StatDisk:
For the above chart: Col 1 is 20H, Col 2 is 23H, Col 3 is 20L, and Col 4 is 23L.
The above data reflects that meals were relatively close in dollar amounts except
for those that were outliers (well above or below the majority and indicated by the last
number listed to the right). Note the outlier for Col 1 is 0 and 50, for Col 2 is 0 and 10,
for Col 3 is 100, and Col 4 is 6. The others are relatively close in number.
Below is the statistical data associated with the box plots.
The above table has four lines of data. The first line is for 20H, second line is for
23H, the third line is for 20L and the fourth line is for 23L. Explanations of the
vocabulary as labeled above the numbers in the table are located at the end of this report.
The above information can also be seen in the STATDISK-Explore Data pages at end of
11

12. this report. We will use this data in the hypothesis testing latter. For now let us look at
Normal Probability Plots associated with data collected.
The following Normal Probability Plots from STATDISK, Data Desk /XL
21.1(DDXL), do not have a straight line and therefore are not normal. The numbers on
the left side of graph represent the values of meals in dollars and the numbers at the
bottom of graph represents the normal scores they fall into. Final conclusions, at end of
report and in hypothesis testing, will explain more. Let us link some fun facts, obtained
during the survey, with this data set to make some since of it.
Normal Probability Plot for 20H
The average time spent eating lunch in the café was about 35 minutes. The higher
prices did not seem to have an affect on the amount of food consumed in the 35 minutes.
Normal Probability Plot for 20L
Average plate size for lunch was 10 inches wide and a good 1.5 inches tall serving
of food. This was concluded as a good serving of food, at a low price.
Normal Probability Plot for 23H
12

13. While eating breakfast, one customer commented during the survey that he had a
very expensive ex-wife when it came to eating out. One could conclude not to take your
ex-wife out to breakfast.
Normal Probability Plot for 23L
Quick and easy breakfast at a low price, we conclude that the day went fast. And
now back to the real facts about the survey. Normal probabilities should have a straight
line through the middle of the graphs. From the normal probability tables above, we can
conclude that the data was not a good sample of a normal distribution. Also, this
information can be seen in the STATDISK-Explore Data pages. Please note the graphs
are the same, but they are set up with different x and y axis.
The following frequencies were computer generated by the STATDISK, Data
Desk /XL 21.1(DDXL). The group represents the dollar amounts, the counts represent the
frequencies and the percentage tells us which has appeared the most.
Frequency for 20H
13

14. Frequency for 20L
Frequency 23H
Frequency 23L
The frequency tables above conclude for 20H customers have chosen meals that
cost $10 or $20 the most, for 20L customers have chosen meals that cost $5 the most,
which is trailed by $4 closely, for 23H customers have chosen meals that cost $15 the
most and for 23L customers have chosen meals that cost $2.99 to $5 the most. We can
conclude that most customers pay no more than $20 for a single meal.
14

15. Histograms are a way one can tell if their data is correct to estimate a population.
A good histogram has a bell shape in the center, but the following histograms do not.
Histogram 20H
0.00
2.00
4.00
6.00
8.00
0
to
9.99
10
to
19.99
20
to
29.99
30
to
39.99
40
to
49.99
50
to
59.99
60
to
69.99
70
to
79.99
80
to
89.99
90
to
100.00
Dollar range
Frequency
Freqency
Histogram 20L
0.00
1.00
2.00
3.00
4.00
5.00
6.00
7.00
0
to
9.99
10
to
19.99
20
to
29.99
30
to
39.99
40
to
49.99
50
to
59.99
60
to
69.99
70
to
79.99
80
to
89.99
90
to
100.00
Dollar range
Frequency
Freqency
Histogram 23H
0.00
1.00
2.00
3.00
4.00
5.00
6.00
0
to
9.99
10
to
19.99
20
to
29.99
30
to
39.99
40
to
49.99
50
to
59.99
60
to
69.99
70
to
79.99
80
to
89.99
90
to
100.00
Dollar range
Frequency
Freqency
15

16. Histogram 23L
0.00
2.00
4.00
6.00
8.00
10.00
12.00
0
to
9.99
10
to
19.99
20
to
29.99
30
to
39.99
40
to
49.99
50
to
59.99
60
to
69.99
70
to
79.99
80
to
89.99
90
to
100.00
Dollar range
Frequency
Freqency
The bottom of the histogram represents the amounts paid with in a dollar range
and the numbers on the left side represents how many customers chose each dollar range.
These histograms are based on a frequency per each dollar range and they are not bell
shaped; therefore, they are a poor representation of how much money a consumers pays
for their meals. These can also be compared with the information seen in the
STATDISK-Explore Data pages.
Let us look at the probability that a customer has paid given amounts for a meal
based on the data collected from the survey’s highs and lows. The enclosed spread sheets
will show different amounts ($20, $15, $5), the z scores, probability area and percentage
of customers who have paid a given amount. The spread sheets include the different
confidence levels of 90%, 95%, and 99% with the margin of error “E” and the confidence
intervals (Mean - E < mean < Mean + E) of a customer who has paid $20, $15, or $5 for a
meal. The samples chosen will help estimate a population by using the mean with a
known standard deviation from the statistical data of survey. The spread sheets are set up
for each day’s highs and lows, again using the codes of 20H, 20L, 23H, and 23L. In each
line of the spread sheets, we will find a given percentage of probability and confidence
interval for the mean.
If a random individual was asked how much he or she has paid for a given meal
(with answers such as the values of $20, $15, and $5) the spread sheet shows the
probability that he or she has paid the given values for a meal. With the confidence
interval of mean plus or minus the margin of error “E”, we can determine if the values are
likely to fall within given range.
In conclusion, the spread sheet for “individual values from a normally distributed
population” is not used. Where as, the spread sheet for “sample of values from a mean for
some sample” can help estimate what the population has paid for a meal.
Now let us look at the main purpose of this survey, the consumer’s preference to
have a choice of complete meals or choice of individual items from menu.
A complete meal or choice of items from menu
Survey on September 20, 2010
16

17. Preferred choice
0
2
4
6
8
10
12
N
o
Answ
er
Strongly
D
is...
D
isagree
N
eutral
Agree
Strongly
A
gree
Respondents choice
Frequencyreflecting
choice
Complete meals
Choose items from
menu
Information regarding meal choice as follows:
Choice Complete meal Choose items from menu
No answer 3 4
Agree 2 2
Neutral 1 3
Strongly Agree 10 7
Strongly Disagree 1 1
Disagree 0 0
Total 17 17
A complete meal or choice of items from menu
Survey on September 23, 2010
17

18. Preferred choice
0
1
2
3
4
5
6
7
N
o
answ
er
Stongly
disagree
D
isagree
N
eutral
Agree
Stongly
agree
Respondents choice
Frequencyreflectingchoice
Complete meals
Choose items from
menu
Information regarding meal choice as follows:
Choice Complete meal Choose items from menu
No answer 3 2
Agree 1 3
Neutral 2 0
Strongly agree 4 6
Strongly disagree 0 0
Disagree 1 0
Total 11 11
Now let us look at the customer’s choice to order individual items or select a pre-
set meal selection. The graphs shows that consumers in the morning of September 23,
wanted to choose individual items from the menu. Where as, afternoon consumers
preferred to choose from complete meals from the menu. The results of this survey
sampling provided evidence that customers have different opinions on how they want to
choose what they eat at different times of the day.
More than one element of life can influence a customer’s choice on the products
they wish to purchase to eat. Full knowledge of how to test data by the use of z-scores, t-
scores and many other tests are necessary. The results concludes that the samples used
here were too small (n<30) and they have outliers (values above or below the majority)
which skewed the data (making it not look like a bell shape). Here are some interesting
18

19. facts: 1) Morning customer wanted to choose individual items from the menu according
to the survey and individual items are expected to be less than $15.00. The hypothesis
test concludes that there is sufficient evidence to support the claim that individual items
are expected to be less than $15.00 and 2) Afternoon consumers preferred to choose from
complete meals from the menu according to the survey and complete meals are expected
to be more than $15.00. The hypothesis test concludes that there is not sufficient evidence
to support the claim that complete meals are expected to be more than $15.00.
Statistics is a new way of thinking about possible outcomes to help understand the
past and predict the future. It is not about the numbers, but it is about the possible out
comes the numbers lead us to.
Description of bias
My sampling of the customers through the survey could be biased due to not
having enough experience in obtaining sufficient information through a survey.
Customers could be more willing to help a college student doing a project for statistics
class, but if I was doing the survey as a general public census, they may not have been
willing to fill out the survey at all.
An incentive to be biased may include that people in a small town will be extra
nice to each other for they live and work together like family. A bias could be developed
due to the fact that the customers may be a regular patron at the restaurant.
Customer may only provide positive and polite feedback leading to a false
representation through the survey. A good bias for corporations is to protect their
consumer’s rights of no salutations at their place of business.
A formal class in survey recovery and public relations could help limit biases
from both customers and presenters of the survey. Public media would provide a way
around systems of protection for consumers. A general street survey could also provide a
wide variety of information if the location’s city and county ordinates allow.
Resources
Wells, Ellen. Survey results. B & J’s Café, 8155 Lander Avenue, Hilmar, CA 95324,
September 20, 2010, 11:00am to 1:45pm.
Wells, Ellen. Survey results. B & J’s Café, 8155 Lander Avenue, Hilmar, CA 95324,
September 23, 2010, 7:00am to 9:45am.
Technologies
Microsoft Excel 2003
STATDISK, Data Desk /XL 21.1(DDXL), Elementary Statistics, 11th
ed., Triola, Mario
F.
STATDISK, Statdisk 11.0.0, Elementary Statistics, 11th
ed., Triola, Mario F.
19