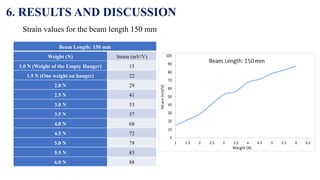
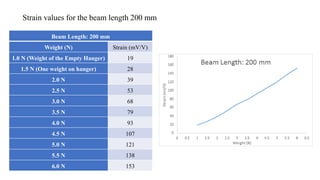
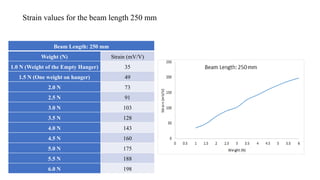
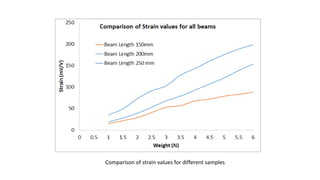
This document outlines an experiment to measure strain on a cantilever beam using resistance strain gauges. It includes an introduction explaining strain measurement using strain gauges, objectives of learning how to use strain indicators and apply uncertainty analysis. The methodology section details the equipment used including a cantilever beam, strain gauges, weights and amplifier. The experimentation section provides steps to mount the beam, zero the amplifier, record strain measurements at different beam lengths and weight amounts. The results section shows tables of strain values measured. Finally, the conclusions note that strain increased with increasing beam length and load amount as expected.

1. PES Institute of Technology and Management, Shivamogga
Department of Mechanical Engineering
Presentation on
TITLE
Presented by
Name 1 4PM……………….
Name 2 4PM……………….
Name 3 4PM……………….
Name 4 4PM……………….
Under the Guidance of
Mr. XXX
XXX Professor
Dept. of Mechanical Engineering
PESITM, SHIVAMOGGA-577204

2. CONTENTS
1. INTRODUCTION
2. OBJECTIVE
3. METHODOLOGY
4. EXPERIMENTATION
5. RESULTS AND DISCUSSION
6. CONCLUSION
7. REFERENCES

3. 1. INTRODUCTION
Strain gauges are used as sensors in many systems to measure forces, moments, and
the deformations of structures and materials. This experiment deals with measuring
the strain in a cantilever beam through the use of four resistance strain gages; two
mounted on top of the beam and two mounted below. A static load will be
incremented at different locations along the beam to produce measurable strains. The
theoretical strain can be found using Equations 1 and 1a.
The stress at the surface of the bending beam can be calculated from the bending moment 𝑀𝑏
and the sectional modulus 𝑊. The stress is given by

4. The bending moment is given by,
The sectional modulus for the rectangular section of width 𝑏 ad height h is
The stress calculated with equation (2) can also be compared to the stress calculated
from the measured strain via Hooke’s law:
In this experiment, you will use a beam with four strain gauges pre-attached and wired to form a
four active leg Wheatstone bridge. The Gunt FL100 measurement amplifier reads the
Wheatstone bridge and outputs the strain as 𝑚𝑉/𝑉. By adjusting the weight mounting point,
three different beam lengths will be tested in this experiment.
Converting from 𝑚𝑉/𝑉 to strain is very straightforward. The equation for the conversion is,

5. 1. Learn about the use of resistance strain gages and Wheatstone bridges
2. Learn to use a static strain indicator
3. Practice the application of Uncertainty Analysis to a physical situation
2. Objectives

6. 1. A metal cantilever beam mounted in a clamp support
2. A C clamp to hold the base to the table,
3. Two 250 Ohm axially mounted strain gages (GF = 2 ± 5%),
4. Two 250 Ohm transversely mounted strain gages (GF = 2 ± 5%),
5. A ten pound set of weights with pan and hanger,
6. NI9219 DAQ Card with built in Wheatstone Bridge and Amplifier,
7. A Digital Multimeter (DMM) with 10 MOhm input impedance (optional)
8. Ruler, micrometer, caliper
9. Weight Scale
3. Apparatus Required

7. Strain in Cantilever Beams
In this work we'll be measuring strain on the surface of a cantilever beam. The applied load at
the beam tip creates a bending moment M, which creates a normal stress and strain
distribution in the beam cross section. The surface strain can be measured at the top or
bottom surface of the beam by measuring the local change in length.
Figure 1.1: Strain in Cantilever Beams

8. Wire is a convenient way to measure strain. When strained, a wire will increase
in length and thin in cross-section. This causes an increase in resistance of the
wire given a constant material resistivity re.
Metal Wire/Foil Strain Gage
𝑅𝑤𝑖𝑟𝑒 =
𝜌𝑒𝐿
𝐴𝑥−𝑠

9. Step 1: Selection of material
Step 2: Surface preparation
Step 3: Marking
Step 4: Cleaning of prepared surface
Step 5: Placing the strain Gauge
Step 6: Pasting the adhesive material to specimen and strain gauge
Step 7: Soldering the strip wires to the mounted strain gauge
Mounting of Strain gauge:
Following are the steps used or lowed during the mounting of strain gauge on the
sample specimens.

10. 1. Remove the cantilever beam from the storage container and mount it on the two metal pins on the
left side of the loading frame.
2. Using the calipers and Allen wrench, adjust the position of the weight mount so that the center of
the weight mount to the front face of the perplex housing around the strain gauges is the length
listed for experimental run 1 in the table below. The 38 mm that is being subtracted is the distance
from the center of the strain gauges to the front face of the perplex housing.
3. Connect the data cable between the strain gauge amplifier and the port on the back of the
cantilever beam.
4. Power up the strain gauge amplifier (switch is on back by power cable)
5. After unit initializes, use the multi-turn potentiometer on the front of strain measurement amplifier
to zero out the display. This balances the Wheatstone bridge.
6. Hang the EMPTY weight hanger on the hook. After the display stabilizes, record the strain
displayed in the table below.
Experimentation

11. 7. Power off the strain measurement amplifier and remove all weights and the weight hanger.
8. Using the calipers and Allen wrench, adjust the position of the weight mount so that the center of the weight
mount to the front face of the perplex housing around the strain gauges is the length listed for experimental
run 2 in the table above.
9. Repeat steps 4 through 6 and record the data in the table below
10.Power off the strain measurement amplifier and remove all weights and the weight hanger.
11.Using the calipers and Allen wrench, adjust the position of the weight mount so that the center of the weight
mount to the front face of the perplex housing around the strain gauges is the length listed for experimental
run 3 in the table above.
12.Repeat steps 4 through 6 and record the data in the table below
13.Power off the strain measurement amplifier and remove all weights and the weight hanger.
14.Replace the weight hanger in the storage container.
15.Disconnect the data cable and replace it in the storage container.
16.Remove the bending beam assembly and replace it in the storage container.

12. 6. RESULTS AND DISCUSSION
Beam Length: 150 mm
Weight (N) Strain (mV/V)
1.0 N (Weight of the Empty Hanger) 15
1.5 N (One weight on hanger) 22
2.0 N 29
2.5 N 41
3.0 N 53
3.5 N 57
4.0 N 68
4.5 N 72
5.0 N 79
5.5 N 83
6.0 N 88
Strain values for the beam length 150 mm

13. Strain values for the beam length 200 mm
Beam Length: 200 mm
Weight (N) Strain (mV/V)
1.0 N (Weight of the Empty Hanger) 19
1.5 N (One weight on hanger) 28
2.0 N 39
2.5 N 53
3.0 N 68
3.5 N 79
4.0 N 93
4.5 N 107
5.0 N 121
5.5 N 138
6.0 N 153

14. Beam Length: 250 mm
Weight (N) Strain (mV/V)
1.0 N (Weight of the Empty Hanger) 35
1.5 N (One weight on hanger) 49
2.0 N 73
2.5 N 91
3.0 N 103
3.5 N 128
4.0 N 143
4.5 N 160
5.0 N 175
5.5 N 188
6.0 N 198
Strain values for the beam length 250 mm

15. Comparison of strain values for different samples

16. 7. CONCLUSIONS
In the present work the following observations were made with respect to static strain measurement
(Over Hanging beam).
1. As the length of the beam increases, the strain value from the strain gauge will also increase.
2. Fabrication work is done with MS material and the strain gauge with 250 Ohm resistance was
mounted on the MS beam and the same beam was used in the strain measurement.
3. As the length of the MS beam increases the deflection of the beam was found to be increasing
prominently which affect the strain gauge mounted on the surface of the MS beam.
4. As the length of the beam increasing the strain value keep on increasing and less values are
identified for the 150mm length sample and higher strain values were identified for the larger or
greater length sample (i.e. 250mm)

17. THANK YOU