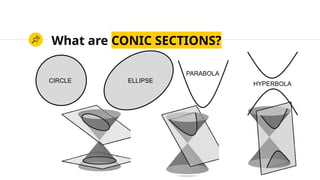
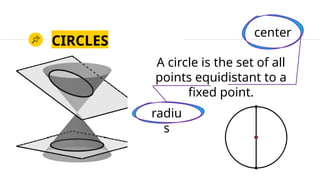
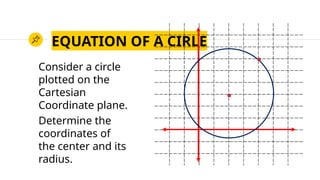
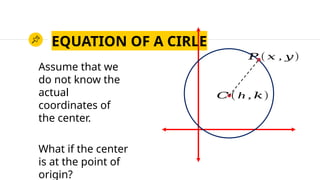
This document outlines session objectives for high school precalculus students focusing on conic sections, particularly circles. Key learning competencies include illustrating different conic types, defining a circle, determining its equations, and graphing. The document explains the properties and equations of circles, including standard and general forms.

1. Precalculus:
CONIC SECTIONS:
CIRCLES

2. Session Objectives
For this two-hour period, SHS students in
Precalculus are expected to develop the following
learning competencies:
1. illustrate the different
types of conic sections:
parabola, ellipse, circle,
hyperbola, and
degenerate cases;
2. define a circle;
3. determine the standard
form and general form of
the equation of a circle;
and
4. graph a circle in a
rectangular coordinate
system.

3. Conic Sections
Intersections of cones and planes
1

4. Starting with Basics
Explain the following mathematical terms:
◉ Undefined Terms in Geometry
◉ Intersecting lines
◉ Parallel lines
◉ Perpendicular lines
◉ Angle
◉ Cone

5. What are CONIC
SECTIONS?
If a plane intersects a double right circular cones, the
intersection is a two-dimensional curve of different types. These
curves are called conic sections.
Also called conics, these different types are:
CIRCLE ELLIPSE
PARABOLA
HYPERBOLA

6. What are CONIC SECTIONS?
CIRCLE ELLIPSE
PARABOLA
HYPERBOLA

7. DEGENERATE CASES

8. CIRCLES
A circle is the set of all
points equidistant to a
fixed point.
radiu
s
center

9. EQUATION OF A CIRLE
Consider a circle
plotted on the
Cartesian
Coordinate plane.
Determine the
coordinates of
the center and its
radius.

10. EQUATION OF A CIRLE
Assume that we
do not know the
actual
coordinates of
the center.
What if the center
is at the point of
origin?
𝐶 ( h , 𝑘)
𝑃 ( 𝑥 , 𝑦)

11. STANDARD FORM
of the equation of a
circle
The standard form of the equation of a circle
whose center is at the origin with radius, r, is
For any circle whose center have coordinates (h, k)
with radius, r, the standard form of its equation is

12. STANDARD FORM
of the equation of a
circle
Give the standard form of the equation of the
circle described in each item below.
1. Center at the origin,
2. and r =
3. and r = 10

13. EQUATION OF A CIRLE
Solve for the equation of the
following circles:
◉ circle A
◉ circle B
◉ center (7, 2), r= 8
−
◉ center (-8,0 ) r= 11

14. Check your
Understanding
Find the center and radius of the given circle.
1. + =100
2. + =
3. + =16
4. = 10
5. =121

15. GENERAL FORM
of the equation of a
circle
The general form of the equation of a circle is
where

16. GENERAL FORM
of the equation of a
circle
Transform the following equations into the general
form:

17. Transforming
equations
Transform the following equations into the
standard form:

18. Transforming
equations
Group the terms based on the
variables.
Complete the square to make
each group of terms a perfect
square trinomial (PST). Add the
constants of the PSTs to the
right side.
Express the PSTs as squares of