1. 기초 수학 스터디삼각 함수

2. 차례기본 정의삼각형 성질삼각형 항등식정의역, 치역

3. 기본 정의hypoppthetaadjSin(theta) = opp / hyp;Cos(theta) = adj / hyp;Tan(theta) = opp / adj = sin(theta) / cos(theta)

4. 기본정의1분면2분면(x, y)rtheta3분면4분면Sin(theta) = y / r;Cos(theta) = x / r;Tan(theta) = y / x;

5. 기본정의주기함수

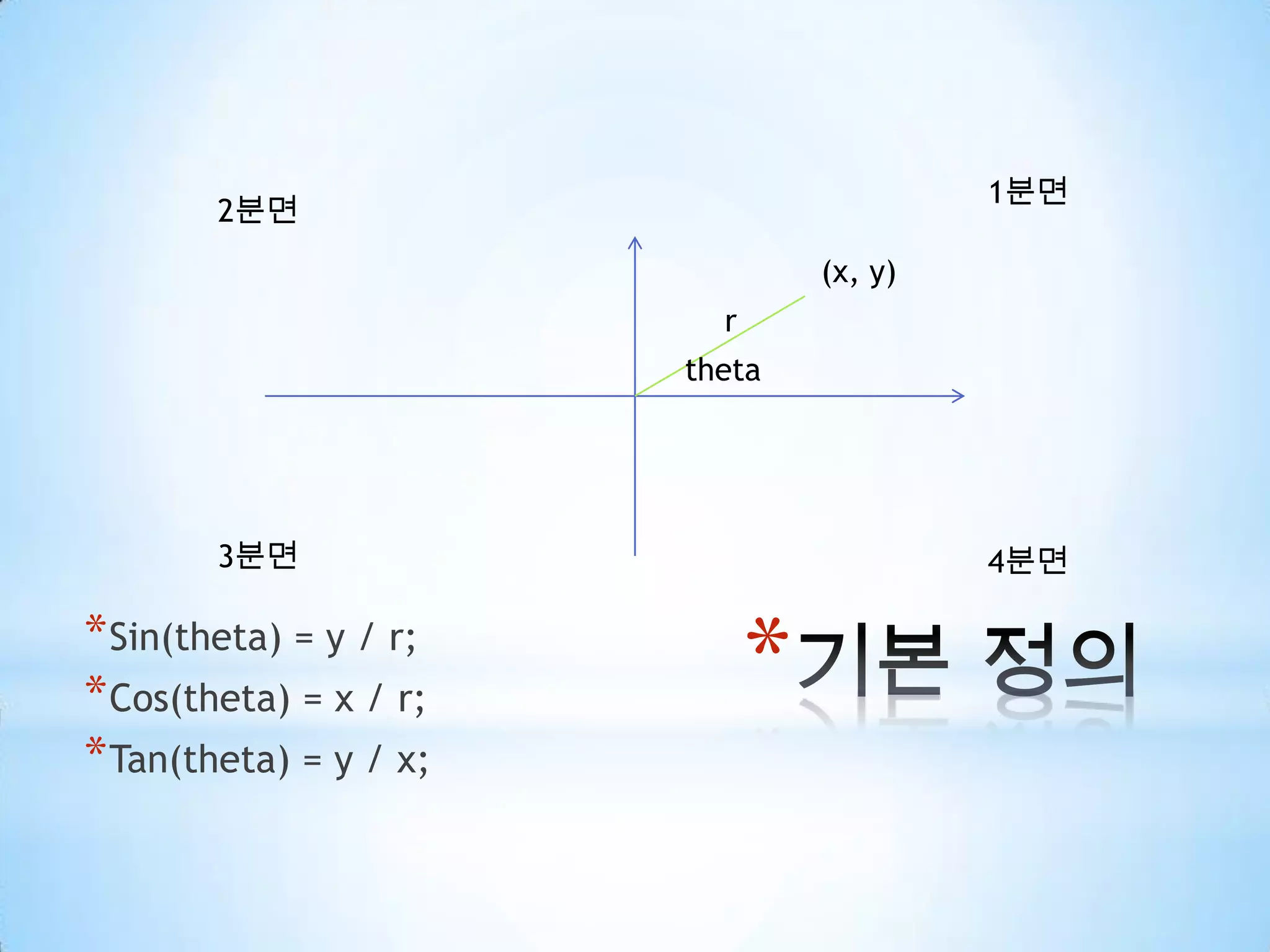
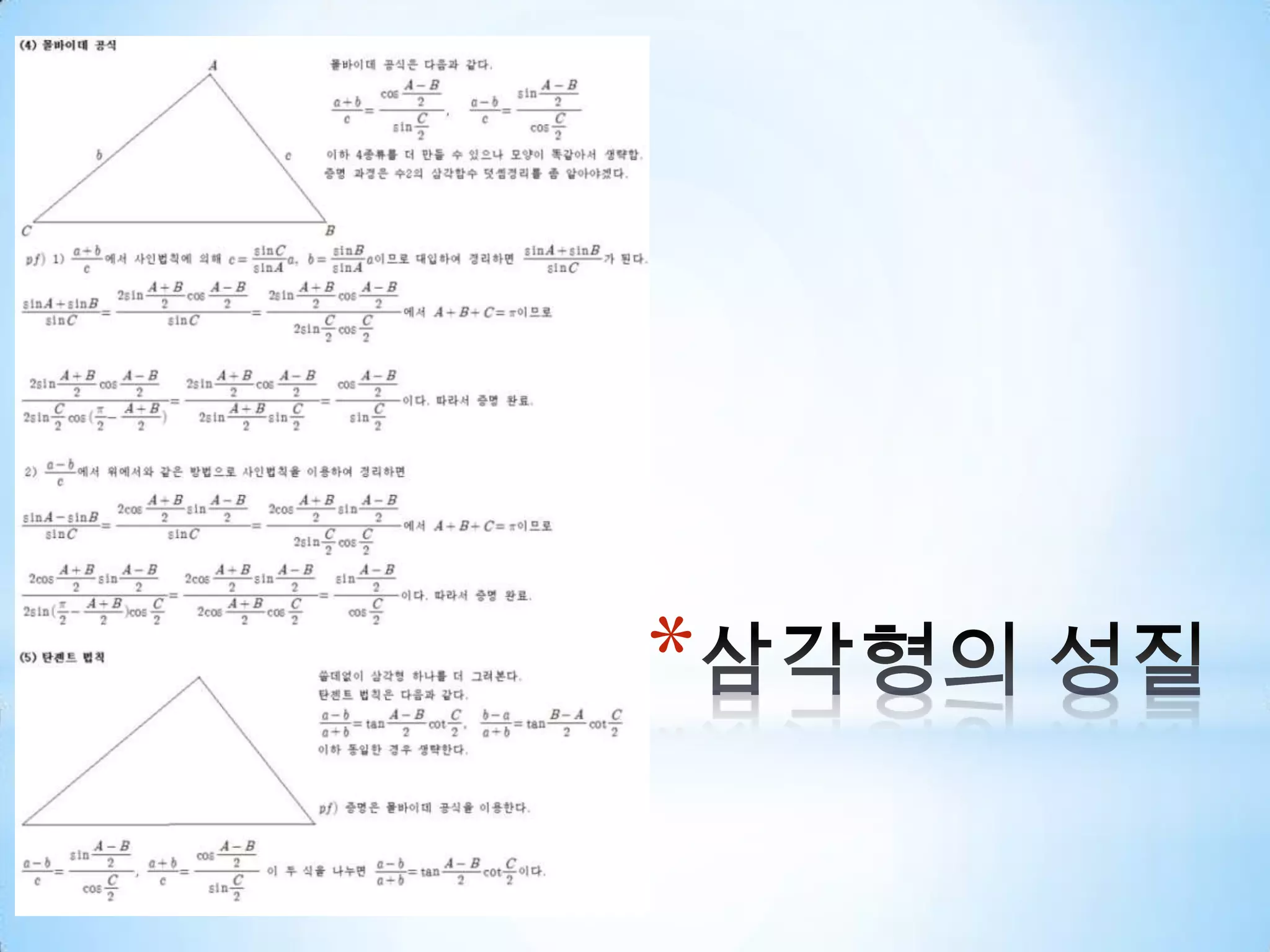
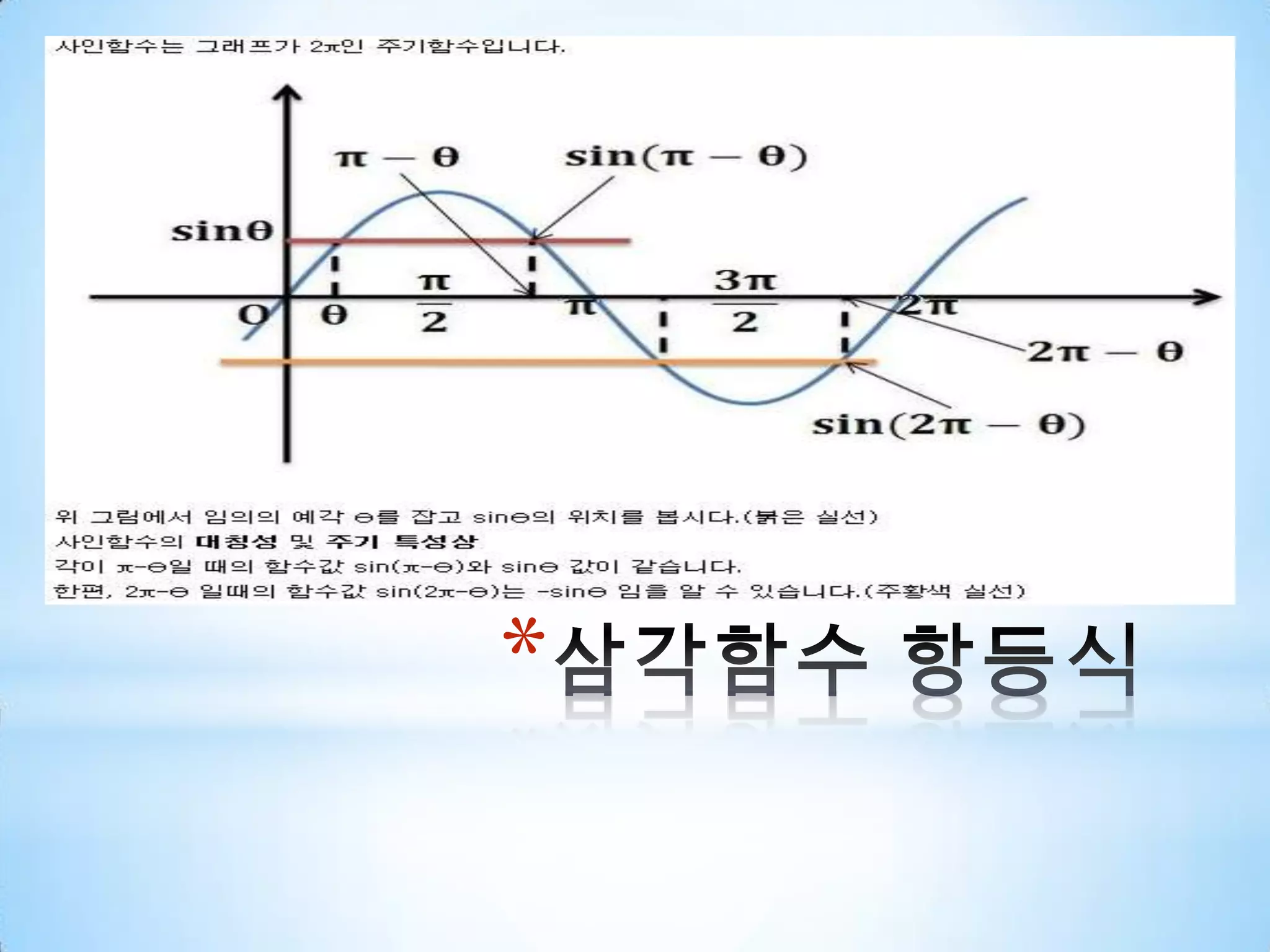
6. 삼각형의 성질βcaαγba/sin(α) = b/sin(β) = c/sin(γ)C^2 = a^2 + b^2C^2 = a^2 + b^2 - (2ab cos(γ)) (제2 cos법칙)나머지 한변의 길이를 구할때, 세 변의 길이로 삼각형의 각을 구할때.

7. 삼각형의 성질

8. 삼각함수 항등식피타고라스 항등식a^2 + b^2 = c^2sin^2(Θ) + cos^2(Θ) = 1tan^2(Θ) + 1 = sec^2(Θ)cot^2(Θ) + 1 = csc^2(Θ)

9. 삼각함수 항등식보각(180 – theta )if #define $ (π/2)sin($-Θ) = adj/hyp = cos(Θ)cos($-Θ) = sin(Θ)tan($-Θ) = cot(Θ)

10. 삼각함수 항등식우함수, 기함수-Θ 에 대한 정의우함수(y축 대칭)cos(-Θ) = cos(Θ)sec(-Θ) = sec(Θ)기함수(원점 대칭)sin(-Θ) = -sin(Θ)csc(-Θ) = -csc(Θ)tan(-Θ) = -tan(Θ)cot(-Θ) = -cot(Θ)

11. 삼각함수 항등식

12. 삼각함수 항등식

13. 삼각함수 항등식합성각sin(a+b) = sin(a)cos(b) + cos(a)sin(b)sin(a-b) = sin(a)cos(b) – cos(a)sin(b)cos(a+b) = cos(a)cos(b) + sin(a)sin(b)cos(a-b) = cos(a)cos(b) – sin(a)sin(b)tan(a+b) = (tan(a)+tan(b))/(1-tan(a)tan(b))tan(a-b) = (tan(a)-tan(b))/(1+tan(a)tan(b))

14. 삼각함수 합성 유도

15. 삼각함수 항등식

16. 삼각함수 항등식배각sin2Θ = 2sinΘcosΘcos2Θ = cos^2Θ-sin^2Θcos2Θ = 1 – 2sin^2Θ= 2cos^2Θ – 1tan2Θ = 2tanΘ / 1-tan^2Θ

17. 삼각함수 항등식반각sin^2Θ = 1-cos2Θ / 2cos^2Θ = 1+cos2Θ / 2

18. 삼각함수 역주기 함수 특성상 정의역한값에 대해 치역이 여러 개로 존재정의역: 값이 정의되는 부분 (x)치역: 정의역에 의해 계산된 값의 집합 (f(x))따라서, sin^-1, cos^-1, tan^-1 함수는 정의역에 따라 여러 개의 값이 나오게 되므로, 이에 대한 함수로 설정하게 된다.