Документ содержит основные принципы и классификации теории систем и системного анализа, исследуя иерархические структуры и взаимодействия в системах. Рассматриваются способы моделирования и оптимизации систем, включая задачи управления запасами, планирования перевозок и стратегического распределения ресурсов. Упоминаются методы комплексного анализа, включая логистические функции и критерию оценки эффективности капитальных вложений.






![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №11
2. Проблемы управления запасами возникают при рассмотрении разнообразных
экономических объектов. При анализе розничной торговли рассматриваются оптимальные
запасы некоторого товара в магазине. Управлять запасами приходится и на производстве,
при планировании работы любой производственной единицы, т. к. чрезмерно большой
запас приводит к нерациональному использованию оборотных средств, а нехватка сырья
или инструмента – приводит к перебоям в производстве.
Рассмотрим хранение единственного продукта, делимого на любые части.
Количество продукта на складе в момент времени t обозначим u ( t ) , при этом продукт
расходуется с постоянно заданной интенсивностью λ . При управлении запасами обычно
принимается следующая стратегия: выбирается уровень запаса u1 такой, что при
достижении этого уровня запаса посылается заказ на пополнение запаса в количестве
u∗ > 0.
Цель исследования систем хранения запасов состоит в выборе наилучшей
стратегии управления запасами. В задачах управления запасами оптимальными
вариантами управления являются те из них, на которых издержки достигают наименьшего
значения.
Следовательно, цель управления запасами – обеспечить минимальные издержки, поэтому
критерий оптимальности запаса товаров определяется функцией издержек, которая имеет
вид:
T
∗
c 0 + c1u + ∫ c 2 u ( t ) dt → min,
(1.2)
0
где T – время производственного цикла; с 0 – стоимость издержек, не зависящая от
объема заказа и возникающая в связи с самим фактом произведения заказа; с1 –
стоимость издержек, пропорциональная количеству заказанного товара; с 2 – стоимость
1
J [u ] =
T
издержек, связанная с хранением единицы товара в течение заданного времени.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-11-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №12
3. При стратегическом планировании организации важной задачей является развитие
материально-технической базы фирмы. При этом цель оптимальности процесса развития
материально-технической базы фирмы можно задать следующим (критерием)
функционалом [5]:
T
J =α∫Vн2 (t )dt −β (T ) → min,
V
(1.3)
0
,
где α β – весовые коэффициенты (α + β =1, α ≥0, β ≥0 ), Vн , V – неосвоенные ОПФ
(капитальные вложения) и освоенные ОПФ соответственно.
Экономический смысл критерия оптимальности заключается в следующем. Минимизация
первого слагаемого в выражении функционала (1.3):
T
J1 =α∫Vн2 (t )dt
0
отражает требование максимальной экономии капитальных вложений. Второе слагаемое в
выражении функционала (1.3)
J 2 =− V (T )
β
V
и его минимизация равносильно максимизации β (t ) значения ОПФ с весовым
коэффициентом β в конце планового периода (0, T ) .
Таким образом, в функционале (1.3) отражены два противоположных требования к
процессу – экономии капиталовложений с одной стороны и увеличению ОПФ
предприятия – с другой.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-12-2048.jpg)

![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №14
5. При стратегическом планировании важной задачей является
распределение ресурсов между производственными подразделениями.
Пусть некоторая функция Эi (Vнi ) отражает увеличение выпуска
продукции на i-м предприятии за счет реализации на нем капитальных
вложений в объеме Vнi . Показатель Эi (Vнi ) является критерием
эффективности капитальных вложений [5].
Пусть количество предприятий данной организации n, а заданный фонд
капитальных вложений A 0 ≤Vнi ≤ A, i =1, n , при этом в оптимальном плане
весь фонд капитальных вложений должен быть полностью реализован.
Предположим, что все функции Эi (Vнi ) возрастающие, то есть
dЭi dVнi >0, i =1, n , то есть эффективность реализации капитальных
вложений возрастает с увеличением их объема.
Математическая модель распределения капитальных вложений между
предприятиями имеет следующий вид:
(
n
∑Эi (Vнi )
i=
1
n
V
∑ нi
i=
1
)
→ max,
(1.5)
= A, Vнi ≥0, i =1, n.
Следовательно, цель распределения капитальных вложений между
предприятиями – добиться максимума суммарной эффективности при
распределении средств между подразделениями организации.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-14-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №15
6. Как известно, процесс контроля состоит из установки стандартов (установки
конкретных целей), измерения фактически достигнутых результатов и проведения
корректировки в том случае, если достигнутые результаты существенно отличаются от
установленных стандартов.
Отклонения от режима планового развития, вызванные изменениями внешней
окружающей среды организации, характеризуются следующими величинами:
∆V ( t ) = V ( t ) − V ∗ ( t ), ∆Vн ( t ) = Vн ( t ) − Vн ∗ ( t ),
где символ (*) означает режим планового развития.
Тогда целью процесса стабилизации планового развития организации
является минимизация отклонения от режима планового развития ОПФ
организации при минимальных затратах инвестиций. Критерий процесса
стабилизации в этом случае примет вид:
∞
[
]
J = ∫ α∆V 2 ( t ) + β∆Vн2 ( t ) dt → min,
0
где α, β – весовые коэффициенты (α > 0, β > 0, α + β = 1) , T = ∞ –
бесконечный горизонт планирования.
(1.6)](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-15-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №16
7. Главная задача организации, занимающейся бизнесом – это получение определенной прибыли пр
ограниченных затратах. Эта ее задача отражается в таких целях, как рентабельность и производительность. Поэтом
целевым критерием системы будет норма рентабельности организации, которая имеет вид [18]:
(1.7)
где
– средняя стоимость ОбПФ,
– средняя стоимость ОПФ,
– цена единично
продукции в момент времени t,
– валовой выпуск в натуральном измерении,
– стоимость ОПФ в момен
времени t,
– стоимость ОбПФ в момент времени t, T – интервал времени (например, один год),
– коэффициен
амортизации ОПФ.
8. Цель оптимального развития экономики однопродуктовой макроэкономической системы – удовлетворени
потребности общества какого-либо региона в данном продукте. Поэтому целевым параметром (критерием) системы
является критерий, предусматривающий рост потребления и возможность наращивать определенный экономически
потенциал к конечному моменту времени, который может быть выражен функционалом следующего вида [5]:
(1.8)
Здесь первое слагаемое представляет собой суммарное взвешенное потребление на промежутке [0,T]
терминальный член имеет смысл накопления производственного потенциала в конечный момент времени. Весовы
коэффициенты
говорят о приоритете, который имеет каждое из этих слагаемых. Если отдается предпочтени
потреблению, то
, а если накоплению производственного потенциала, то
. Подынтегральное выражени
– дисконтированное потребление,
– функция полезности, – коэффициент дисконтирования,
стоимость ОПФ в момент времени T и непроизводственное потребление
.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-16-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №17
Логистическая функция описывается уравнением вида [6]:
(2.1)
где
– численность популяции в единице объема выпуска системы в момент времени t;
– максимальная численность популяции; a, b – константы.
X
Из рис. 2.1 видно, что логистическая кривая начинается в
точке
, симметрична
и имеет точку перегиба с координатами
Константа a определяет положение логистической кривой по
времени (сдвиг влево или вправо),
константа b – наклон кривой. Эти
константы очень легко вычисляются по формулам:
t
0
t1
ln a/b
Рис. 2.1
.
(2.2)
t2](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-17-2048.jpg)










![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
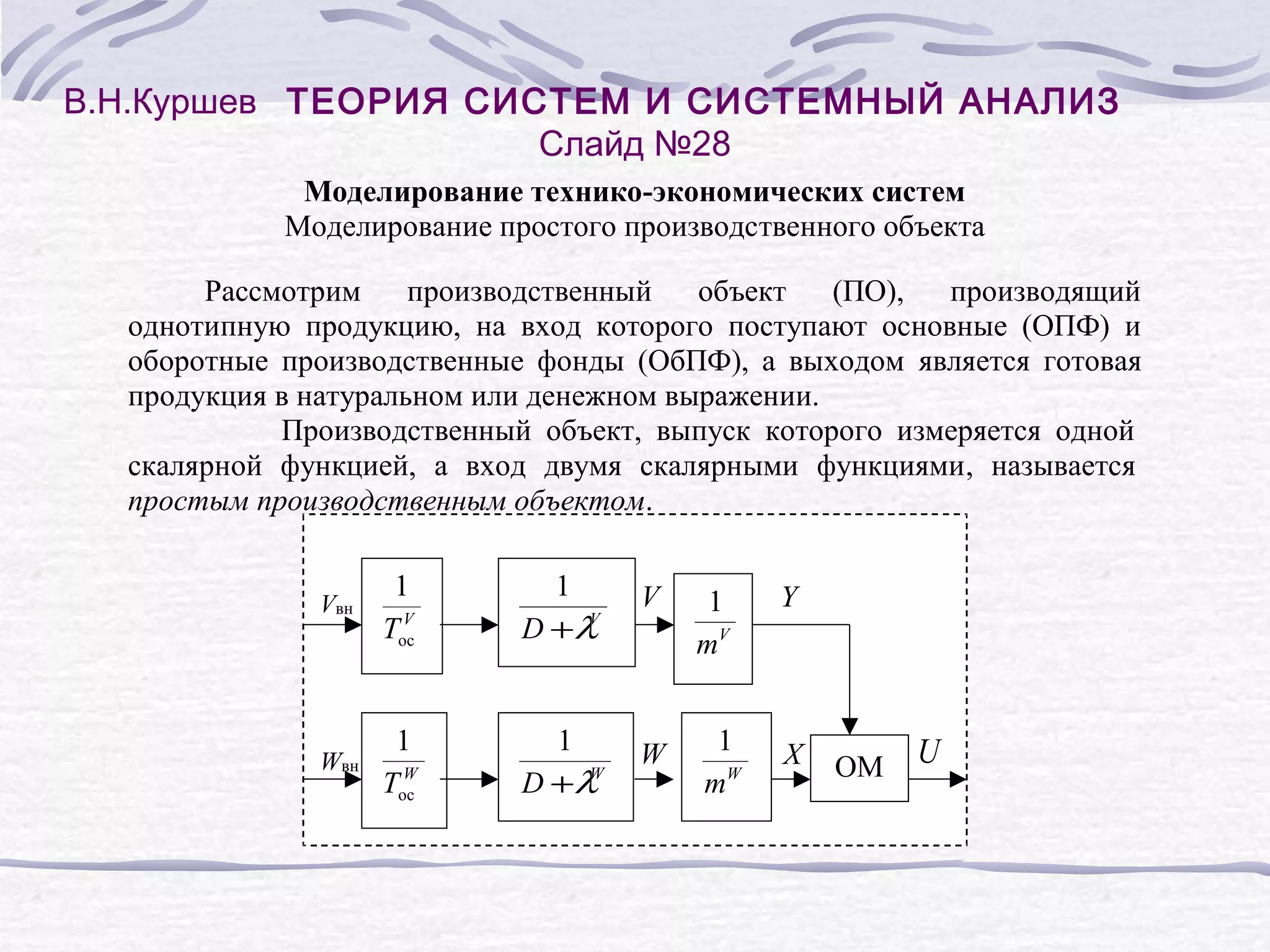
Слайд №29
В соответствии с функционально-структурной схемой движение в процессе
производства ОПФ и ОбПФ и выпуск готовой продукции можно записать так:
dV (t )
1
[
=− V V (t ) + V Vвн (t ), V (t ) t = = 0 , t ∈0, T ],
λ
V
0
dt
Tос
dW (t )
1
=− W W (t ) + W Wвн (t ), W (t ) t = = 0 ,
λ
W
0
dt
Tос
X (t ) = (t ) m W (t ) , Y (t ) = (t ) mV (t ) ,
W
V
)
U (t ) =(1 −ρ X (t ) +ρ (t ),
Y
1
Y
при X (t ) = (t ),
0
Y
при X (t ) < (t ),
ρ=
V
W
V
W
где λ , λ – коэффициенты выбытия ОПФ и ОбПФ; Tос , Tос – время
освоения неосвоенных ОПФ и ОбПФ отрасли; T – горизонт планирования.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-29-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
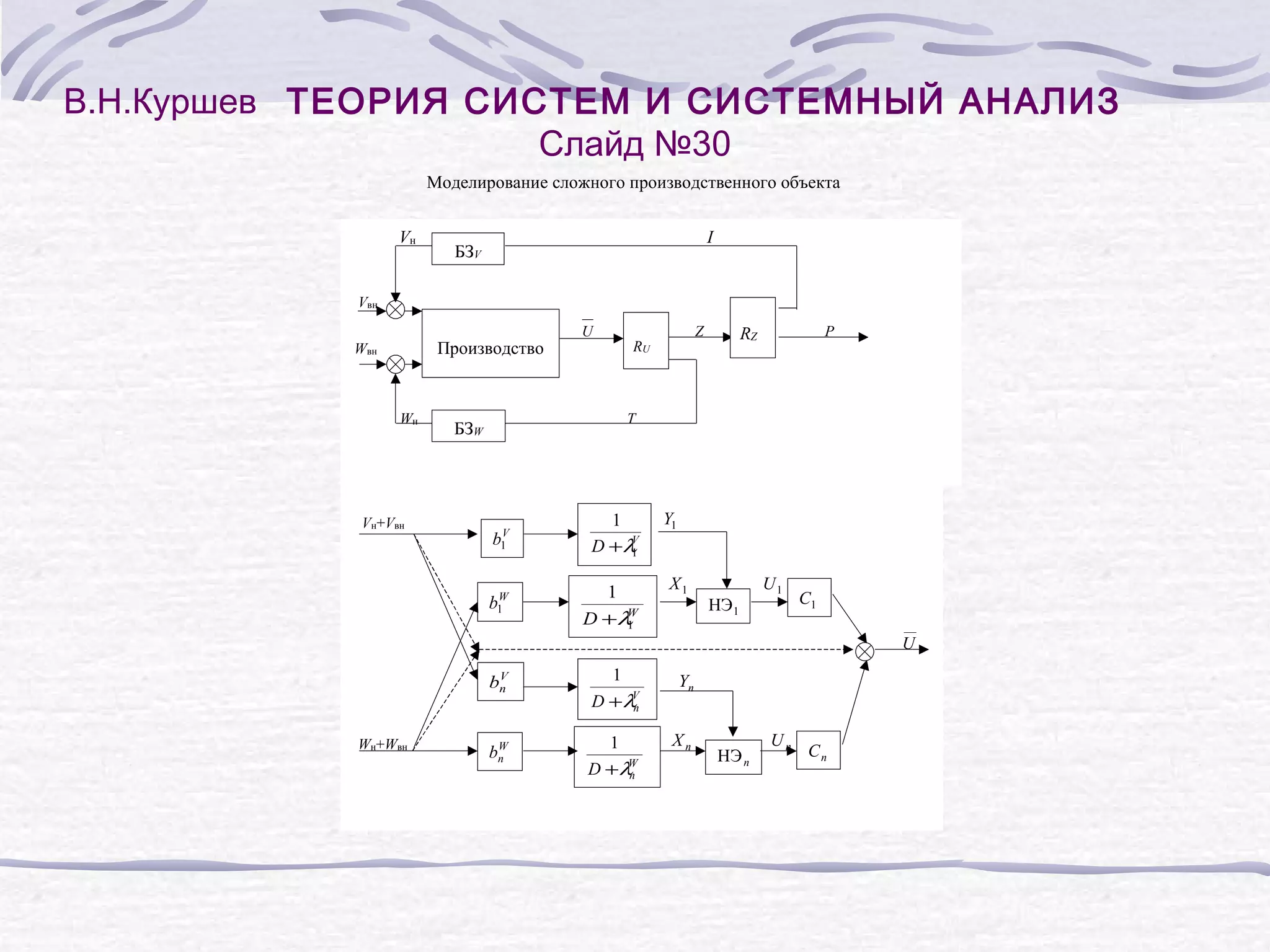
Слайд №31
Математическая модель отрасли с учетом структур ее подразделений:
dYi (t )
[0 ,
= λYi (t ) +iV [ н (t ) + вн (t )] Yi (t )t = =0i , i =, n, t ∈, T ]
−V
b V
V
,
Y
1
i
0
dt
dX i (t )
= λ X i (t ) +iW [ н (t ) + вн (t )] X i (t )t = = 0i , i =, n,
−W
b W
W
,
X
1
i
0
dt
(1 ρ
U i (t )= − )X i (t )+ Yi (t )
ρ ,
n
U (t ) = C iU i (t )
.
∑
i=
1
Математическая модель замкнутого производственного объекта в
матричной форме:
dY (t )
= Λ (t )+ V [ н (t )+вн (t )] Y (t )t = =0 ,
−V Y
B V
V
,
Y
0
dt
dX (t )
= Λ (t )+ W [ н (t )+ вн (t )] X (t )t = = 0 ,
−W X
B W
W
,
X
0
dt
U (t )= − )X (t )+ Y (t ),
(1 ρ
ρ
U (t ) = (t )
CU ,
Wн (t ) =U (t )
a
,
Vн (t ) = ( − ) (t )
d1 aU ,
P(t ) = − )( − ) (t )
(1 d 1 a U .
Эти уравнения получены без учета запаздывания в освоении ОПФ и
I
T
ОбПФ, т. е. когда Vн (t )=(t ), Wн (t )= (t ).](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-31-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №32
Моделирование запаздывания при освоении капитальных вложений
и производственных затрат
Математическую модель замкнутого производственного объекта с
учетом инерционного запаздывания ввода основных фондов и процесса
производства в следующем виде:
dY ()
t
=V Y () B V Vн () Y ()= Y0 ,
− t + t,
Λ
t t 0=
dt
dX ()
t
=W X () B W Wн () X ()= X 0 ,
− t +
Λ
t,
t t 0=
dt
dVн ()
t
′
=I () Vн () Vн ()= Vн 0 ,
ζ t −t ] t t 0 =
[
,
dt
dWн ()
t
′
′
[
=T () Wн () Wн ()= Wн0 ,
ζ t −t ]
,
t t 0=
dt
)
U () ( − () ρ ,
t = ρt +()
1
X
Yt
1 при
t =,
t
X () Y ()
ρ
=
0 при X () Y ()
t <,
t
U () CU ()
t = t,
T () aU ()
t =t,
′ ин ′
′
=′ ′ ин
=′
где ζ1 τ, ζ 1 τ.
I () d ( − ()
t = a) t ,
1
U
( U
P() ( −1 − ()
t = d ) a) t ,
1](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-32-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №33
Моделирование многоотраслевой экономики
Математическую
модель
в
матричной
форме
замкнутой
многоотраслевой экономики:
dYi ( t )
= −ΛVi Yi ( t ) + BiV Vн i ( t ) + Vвн i ( t ) , Yi ( t ) t =t = Y0i , i = 1, s,
0
dt
dX i ( t )
= −ΛW X i ( t ) + BiW Wн i ( t ) + Wвн i ( t ) , X i ( t ) t =t = X 0i , i = 1, s,
i
0
dt
U i ( t ) = CiU i ( t ) , U i ( t ) = (1 − ρ ) X i ( t ) + ρYi ( t ) , i = 1, s,
[
]
[
]
s
Wнi ( t ) = ∑ aij U j ( t ) , i = 1, s,
j =1
Vнi ( t ) = ∑ d ij U
j =1
s
s
l =1
j ( t ) − ∑ a jl U l ( t ) ,
Pi ( t ) = U i ( t ) − ∑ a ij U j ( t ) − ∑ d ij U
j =1
j =1
s
i = 1, s,
s
s
j
l =1
( t ) − ∑ a jl U l ( t ) ,
i = 1, s.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-33-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
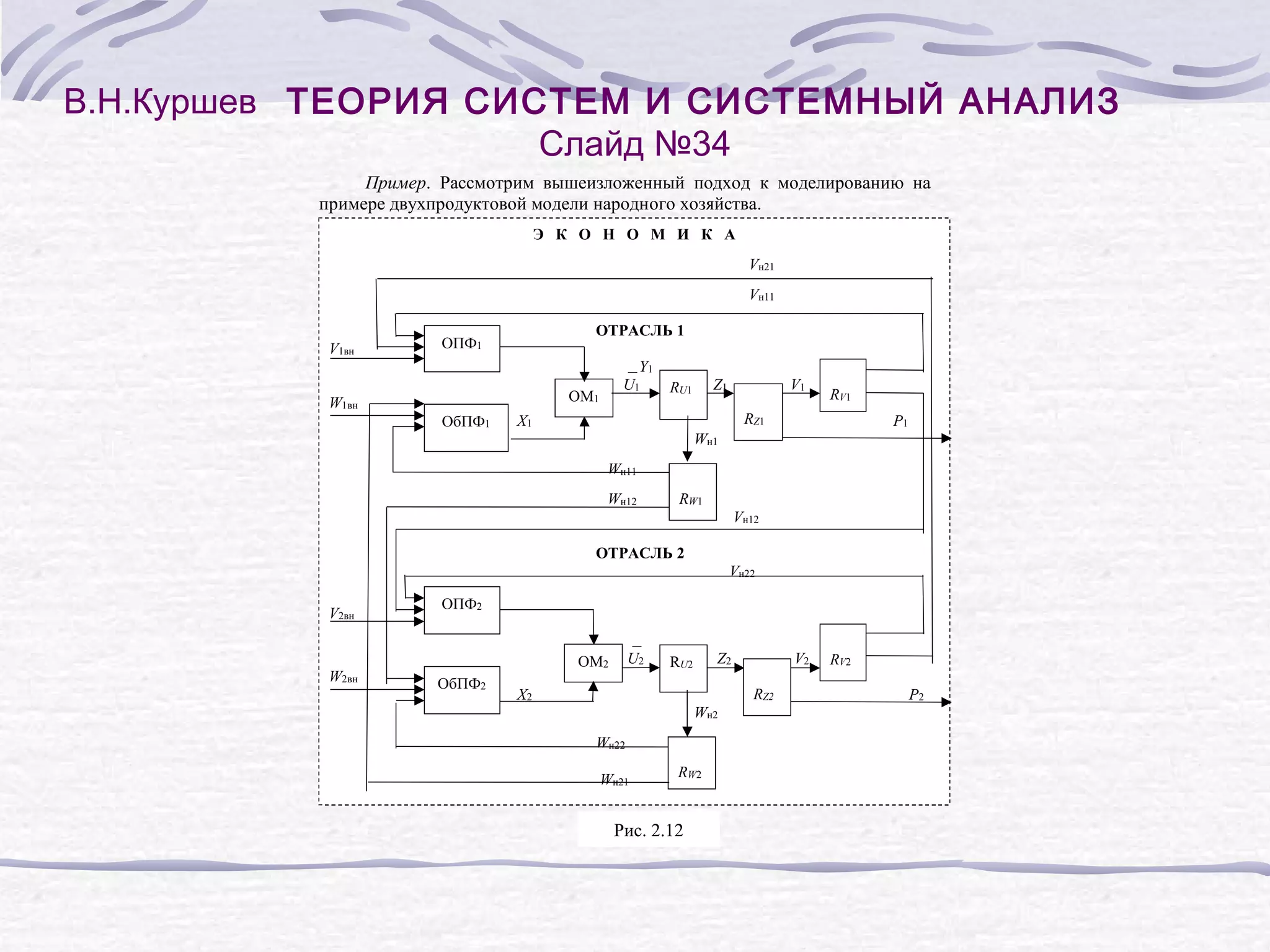
Слайд №35
Математическая модель в матричной форме замкнутой двухотраслевой
экономики:
dYi ( t )
V
= −Λi Yi ( t ) + BiV Vн i ( t ) + Vвнi ( t ) , Yi ( t ) t =t = Y0i , i =1, 2,
0
dt
dX i ( t )
W
= −Λi X i ( t ) + BiW Wн i ( t ) + Wвнi ( t ) , X i ( t ) t =t = X 0i , i =1, 2,
0
dt
U i ( t ) = (1 − ρ) X i ( t ) + ρYi ( t ), i =1, 2,
1 при X i ( t ) = Yi ( t ),
ρ =
0 при X i ( t ) < Yi ( t ),
U i ( t ) = CiU i ( t ), i =1, 2,
[
]
[
]
Wн1 ( t ) = a11U 1 ( t ) + a12 U 2 ( t ),
Wн 2 ( t ) = a21U 1 ( t ) + a22 U 2 ( t ),
Vн1 ( t ) = [ d11 (1 − a11 ) − d12 a21 ]U 1 ( t ) + [ d12 (1 − a22 ) − d11a12 ]U 2 ( t ),
Vн 2 ( t ) = [ d 22 (1 − a22 ) − d 21a12 ]U 2 ( t ) + [ d 21 (1 − a11 ) − d 22 a21 ]U 1 ( t ),
P1 ( t ) = [(1 − a11 )(1 − d11 ) + d12 a21 ]U 1 ( t ) − [ a12 (1 − d11 ) + d12 (1 − a22 ) ]U 2 ( t ),
P2 ( t ) = [(1 − a22 )(1 − d 22 ) + d 21a12 ]U 2 ( t ) − [ a21 (1 − d 22 ) + d 21 (1 − a11 ) ]U 1 ( t ).](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-35-2048.jpg)

![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №37
Модель ПО с обратной связью по ИД:
dY (t ) V
[0
+ Y (t ) = V (t ), Y (t ) t = = 0 , t ∈ , T ],
λ
u
Y
0
dt
dX (t ) W
+ X (t ) = W (t ), X (t ) t = =X 0 ,
λ
u
0
dt
uV (t ) = V (t )Y (t ), uW (t ) = W (t )X (t ),
ξ
ξ
( ρ
U (t ) =1 − )X (t ) +ρ (t ),
Y
1
Y
при X (t ) = (t ),
ρ=
0
Y
при X (t ) < (t ),
или, исключая управления,
dY (t )
V
[0
=ξ (t ) − V Y (t ), Y (t ) t = = 0 , t ∈ , T ],
λ
Y
0
dt
dX (t )
W
=ξ (t ) − W X (t ), X (t ) t = =X 0 ,
λ
0
dt
(
)
U (t ) =1 −ρ X (t ) +ρ (t ).
Y
(
(
)
)](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-37-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №38
Инновационная
деятельность
увеличивает
эффективность
использования внешних поступлений как основных, так и оборотных
производственных фондов:
dY () V
t
[,T ]
+ () u V () v вн () Y ()= Y0 , t ∈
Y t = +t ,
t
t t 0=
0 ,
dt
dX () W
t
+ () u W () w вн () X ()= X 0 ,
X t =t + t ,
t t 0=
dt
U () (− () Y ()
t = ) t +t ,
1
X
λ
λ
ρ
ρ
V
W
t =t
t =t
где vвн () Vвн ()Tос , wвн () Wвн ()Tос – потоки внешних поступлений ОПФ
V
() t , w t = t w t ; V W
t = t vвн () вн () W () вн () Tос , Tос – время освоения
и ОбПФ; v вн ()
неосвоенных ОПФ и ОбПФ отрасли.
µ
Vвн
µ
1
µ
()
t
V
λ
ξ
V
D+
() V
t
u
1
V
Tос
W
µ
()
t
U
λ
W
D+
W
Tос
W
Y
ρ
1−
ρ](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-38-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №39
В частном случае, когда величины внешних поступлений ОПФ и ОбПФ
и обобщенные показатели инновационной деятельности постоянны и
V
const и Wвн =
const , ξ =
const и
являются известными величинами ( Vвн =
W
ξ =const ), система уравнений примет вид:
V
dY (t )
exp(ξ t )
V
V
( λ
[
=ξ − )Y (t ) + V V Vвн (t ), Y (t ) t = = 0 , t ∈0, T ],
Y
0
dt
Tос m0
W
dX (t )
exp(ξ t )
(W λ
=ξ − W )X (t ) + W W Wвн (t ), X (t ) t = =X 0 .
0
dt
Tос m0
U (t ) =1 −ρ X (t ) +ρ (t ),
(
)
Y
1
Y
при X (t ) = (t ),
ρ=
0
Y
при X (t ) < (t ),
Аналитические зависимости мощности и выпуска ПО с учетом ИД
СКБ:
[(
)]
V
Y (t ) = 0 exp ξ − V t +
Y
λ
[(
Vвн
V
λ Tос mV
0
)]
V
W
X (t ) =X 0 exp ξ − W t +
λ
Wвн
{exp(ξ t ) −exp[(ξ
W
λ Tос mW
0
W
V
V
) ]}
− V t , t ∈0, T ],
λ
[
{exp(ξ t ) −exp[(ξ
W
(
)
U (t ) =1 −ρ X (t ) +ρ (t ),
Y
1
Y
при X (t ) = (t ),
ρ=
0
Y
при X (t ) < (t ),
W
) ]}
−W t ,
λ](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-39-2048.jpg)

![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №41
КАЧЕСТВЕННЫЙ АНАЛИЗ МОДЕЛЕЙ РАЗВИВАЮЩИХСЯ
ЭКОНОМИЧЕСКИХ СИСТЕМ
Исследование устойчивости развивающихся систем
Рассмотрим развивающуюся экономическую систему, описываемую дифференциальными нелинейными
уравнениями второго порядка следующего вида [6]:
dX i
= f i ( X ) , i = 1,2,
dt
где f i ( i = 1,2 ) – непрерывные функции, определяемые в некоторой области R
двухмерного евклидова пространства и имеющие в этой области
производные порядка не ниже первого. Состояние системы в каждый момент
времени определяется парой значений неизвестных ( X 1 , X 2 ) .
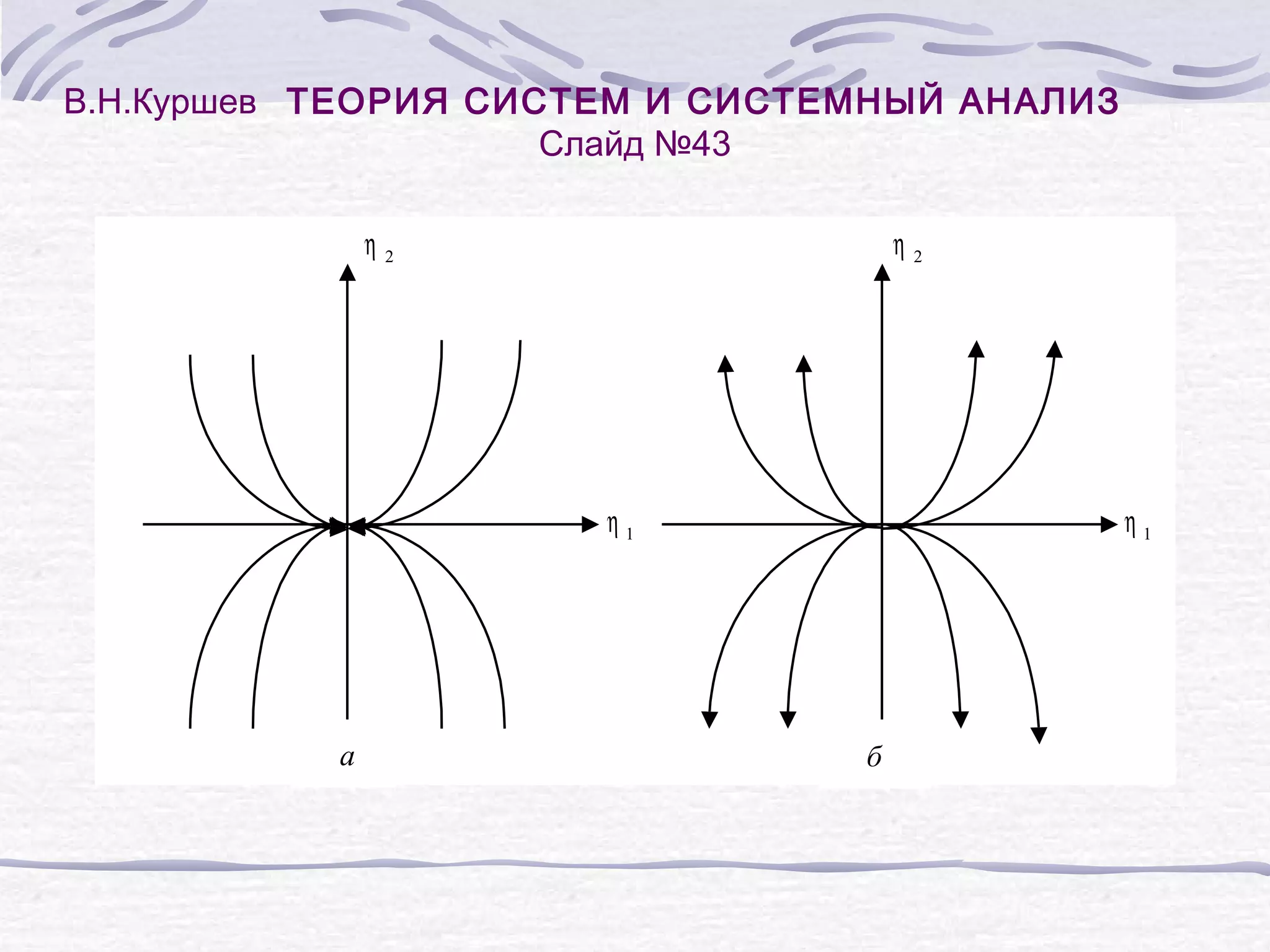
Под устойчивостью системы понимается свойство системы
возвращаться к состоянию установившегося равновесия после устранения
возмущения, нарушившего указанное равновесие.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-41-2048.jpg)

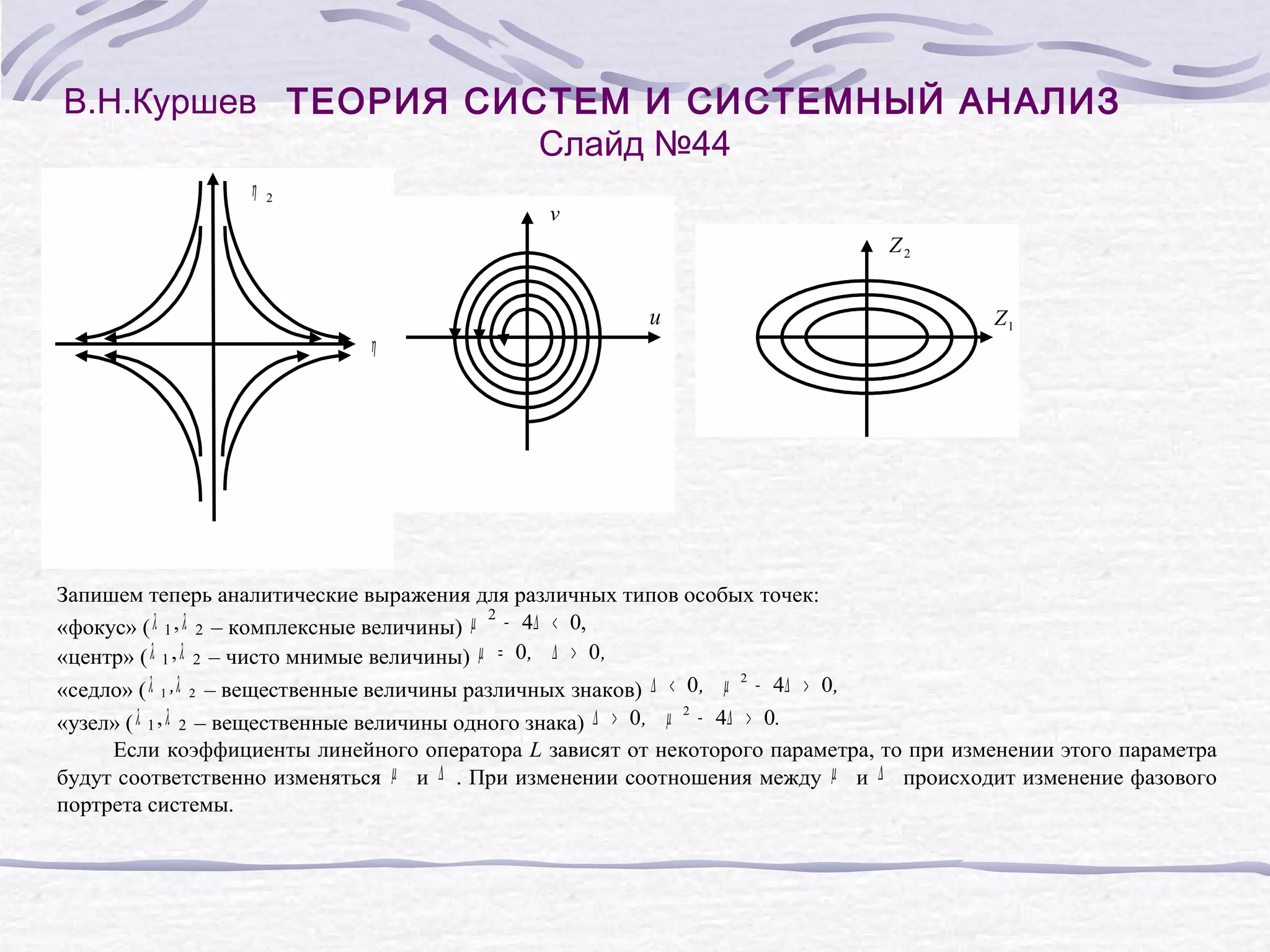









![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №55
Сбалансированный рост
в однопродуктовой макроэкономической системе
Рассмотрим однопродуктовую модель развития региона или отрасли.
Взаимосвязь производства и потребления, а также динамику таких
экзогенных факторов, как рабочая сила и основные производственные
фонды, можно отразить с помощью моделей агрегированных систем.
Наиболее простая модель взаимодействия между производством и
потреблением предложена Ф. Рамсеем [6]. Уравнения модифицированной
модели можно записать в следующем виде:
X (t ) = aX (t ) + Z (t ), Z (t ) =Vн (t ) + P(t ),
X (t ) = F (V , L, t ), L(t ) = L0 exp(ηt ),
•
V
V (t ) =−Λ V (t ) + qVн (t ), V ( 0 ) =V0 ,](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-55-2048.jpg)

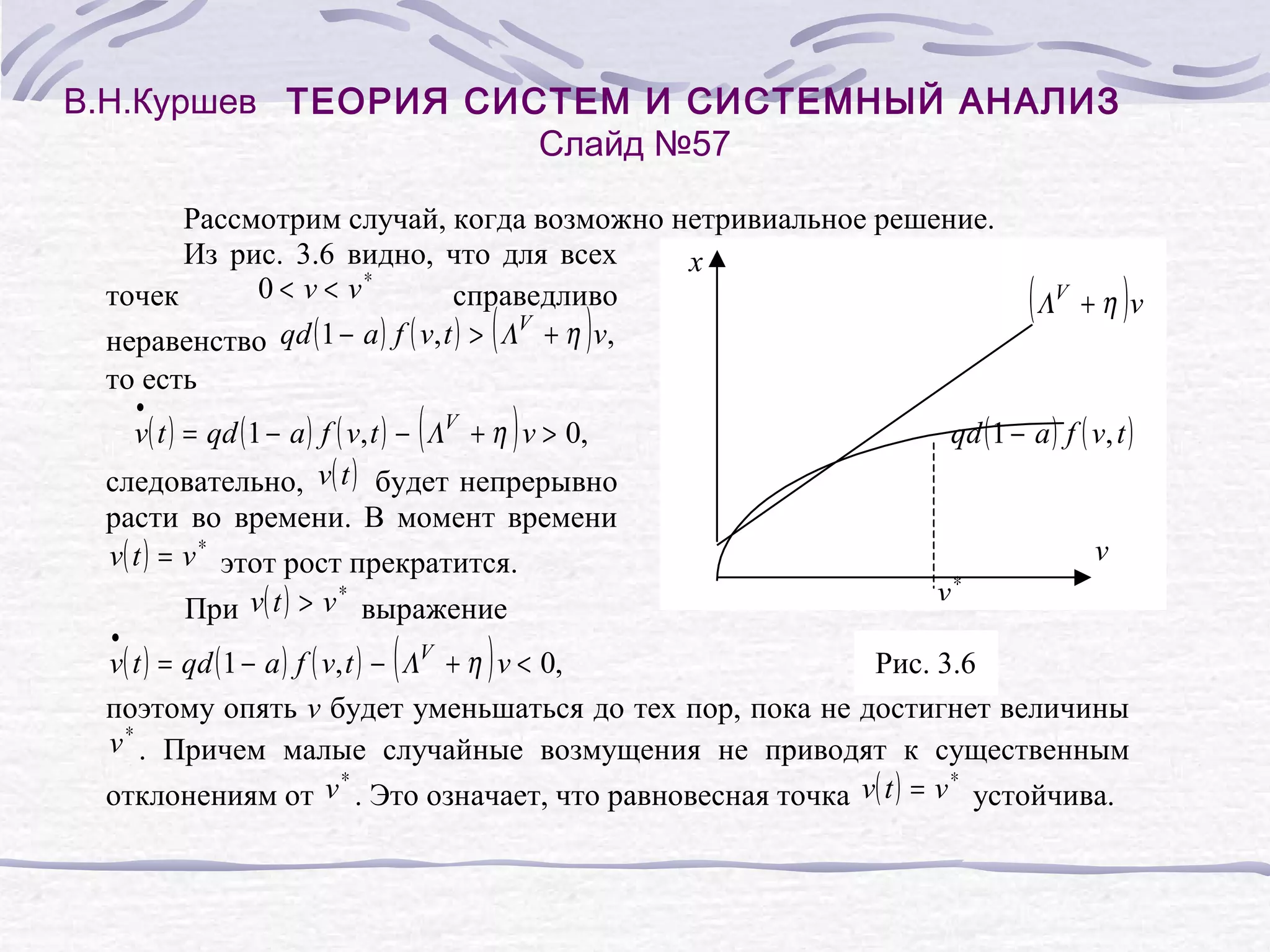

![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №59
АНАЛИЗ ОПТИМАЛЬНОГО РАЗВИТИЯ ЭКОНОМИЧЕСКИХ
СИСТЕМ
Исследование оптимального развития однопродуктовой макромодели
экономической системы
Рассмотрим экономику, модель которой описывается следующими уравнениями:
•
v(t ) = (λ+ )v(t ) +q(1 − )(1 − ) f (v, t ),
− η
u
a
v(0 ) = 0 .
v
Ограничение на управление u =d :
0≤ ≤,
u 1
а ограничения на ОПФ заменим ограничениями на фондовооруженность:
v(t ) ≥ з (t ).
v
Задача оптимизации данной экономики состоит в том, чтобы найти
такое управление процессом развития, которое обеспечило бы наибольшее
среднедушевое потребление на рассматриваемом интервале времени [0,T] с
учетом дисконтирования потребления, то есть
T
P(t )
J =∫
exp(− t ) dt.
δ
L(t )
0](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-59-2048.jpg)
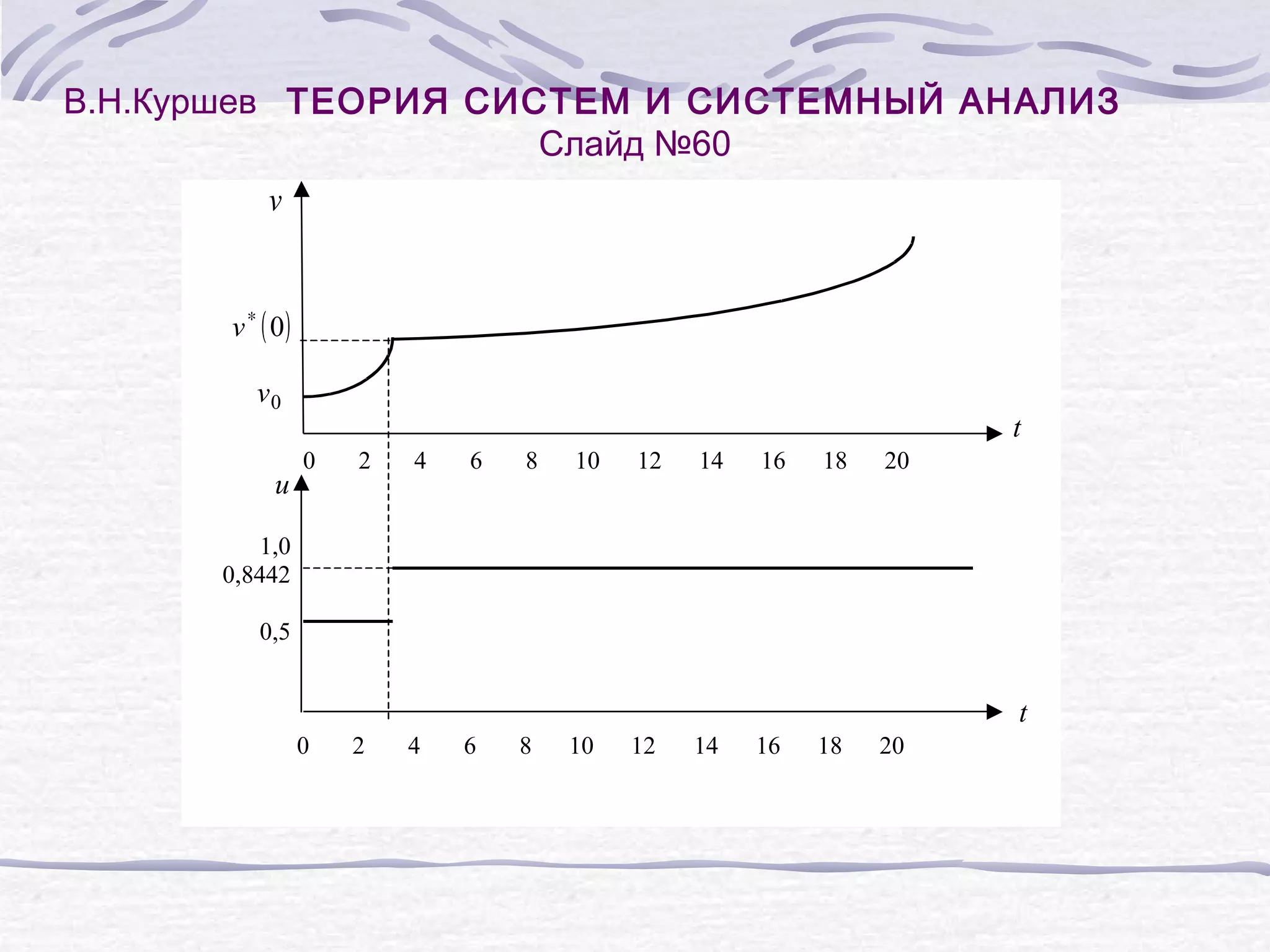
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №61
Однопродуктовая макросистема. Пусть управляемая система представляет
собой экономику региона или отрасли, моделируемую с помощью
однопродуктовой модели, то есть процесс экономического развития задается
уравнением
•
(
v(t ) =−λ+η) v(t ) +q[(1 −a ) f (v, t ) − p(t )],
v(0 ) =v0 ,
где p(t ) – управляющая функция.
Допустимым управлением назовем любую кусочно-непрерывную
функцию p(t ) , которая удовлетворяет уравнению и граничному условию
(
0 ≤ p(t ) ≤(1 −d )(1 −a ) f (v, t ), t ∈0, T ).](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-61-2048.jpg)
![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №62
Теперь надо уточнить понятие оптимальности. Очевидно, критериев
оптимальности может быть множество. Рассмотрим наиболее общий
критерий – функционал благосостояния системы в виде:
T
J =∫g [ p (t )]exp(− t ) dt.
δ
0
Задача оптимизации состоит в выборе такого управления p(t ) в
заданном интервале времени, чтобы соответствующее ему решение
уравнения доставляло максимум функционалу.
В случае конечного горизонта планирования должны выполняться
v
условия на конце траектории v(T ) = 1 . Для бесконечного горизонта
планирования интеграл благосостояния может оказаться расходящимся,
поэтому необходимо задавать ограничения на начальные условия
v(0) = 0 ≤ ,
v
v
то есть начальная капиталовооруженность должна быть меньше предельно
достижимой.](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-62-2048.jpg)

![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
Слайд №64
Введем, как и ранее, критерий – функционал благосостояния системы в
виде:
T
(
J =∫g [ϕv1 , v 2 , v н1 , v н2 )]exp(− t )dt + [v1 (T ), v 2 (T )].
δ
G
0
Тогда задачу оптимизации можно сформулировать так: среди
1
допустимых управлений v н j , j = ,2 , найти такое, чтобы соответствующее
ему решение системы уравнений доставляло максимум функционалу.
Для решения поставленной задачи воспользуемся принципом
максимума. Функция Гамильтона в этом случае будет
(
H = (− t ){g [ϕv1 , v2 , vн1 , vн2 )] + 1 (q1vн1 − v1 ) + 2 (q2 vн2 − v2 )},
exp δ
b
γ
b
γ
b
δ
b
δ
где ψ(t ) = 1 (t )exp(− t ), ψ (t ) = 2 (t )exp(− t ).
1
2
Оптимальное управление определим так:
∂
H
∂
H
=,
0
=,
0
∂ н1
v
∂ н2
v](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-64-2048.jpg)




![В.Н.Куршев ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ
№69
Слайд
4.4. Планирование оптимального развития основных фондов предприятия
Уравнение материального баланса ОПФ будет иметь вид [4]:
(4.82)
Начальное значение ОПФ будем считать заданным
Следовательно,
описывает состояние процесса
а функцию
будем считать управлением.
Критерий оптимальности:
развития
(4.83)
ОПФ,
(4.84)
где
– весовые коэффициенты
Ставится следующая задача: среди всех допустимых управлений
найти такое, чтобы функционал (4.84) достигал наименьшего значения с учетом
связей (4.82), (4.83).
Введем функцию Гамильтона
(4.85)
где
– множитель Лагранжа, который определяется из сопряженной
системы
(4.86)](https://image.slidesharecdn.com/random-140218050001-phpapp02/75/slide-69-2048.jpg)

