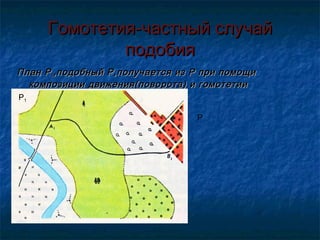
Документ представляет собой проектную работу ученика 9-го класса, посвященную геометрическим преобразованиям плоскости. В работе описаны основные виды преобразований, такие как движения, подобие и гомотетия, с объяснением их свойств и применения. Особое внимание уделяется аффинным преобразованиям и их значению в математической культуре.