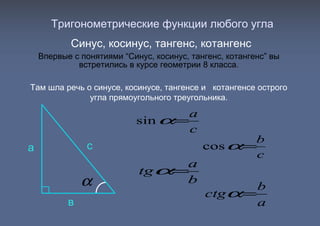
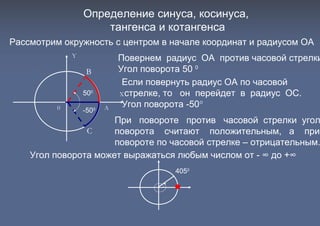
Документ обсуждает тригонометрические функции синус, косинус, тангенс и котангенс, начиная с их определения в контексте острых углов прямоугольного треугольника. Также рассматривается угловая мера и поворот радиуса в окружности, а также классификация углов по четвертям координатной плоскости. Подробно описываются свойства углов и их влияние на значения тригонометрических функций.