Downloaded 66 times
圧縮センシングとネットワーク化制御
- 1. 圧縮センシングと ネットワーク化制御 永原正章 （京都大学）
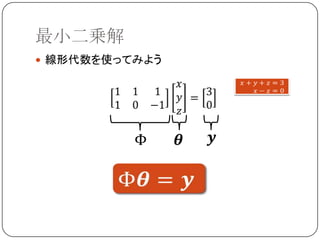
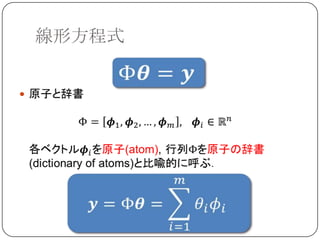
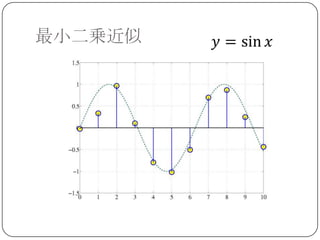
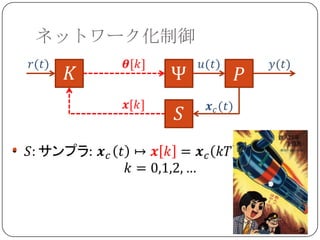
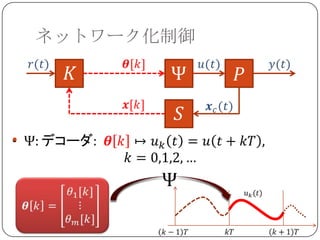
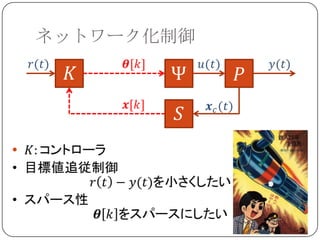
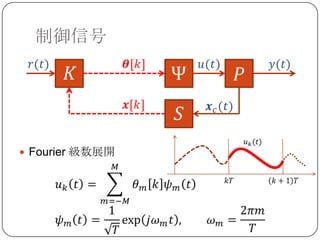
- 2. もくじ 連立方程式の復習 最小ノルム解 最小二乗近似解 正則化最小二乗法 Sparse Land での正則化最小二乗法 圧縮センシングの基礎 ネットワーク化制御への応用 まとめ
- 3. もくじ 連立方程式の復習 最小ノルム解 最小二乗近似解 正則化最小二乗法 Sparse Land での正則化最小二乗法 圧縮センシングの基礎 ネットワーク化制御への応用 まとめ
- 4.
- 5. 連立方程式 変数の数＞方程式の数 →解は無数に存在 犯罪捜査に例えると．．． 方程式の解＝真犯人 方程式＝証拠 証拠が少ないと，犯人を特定することはできない．
- 6.
- 7.
- 8.
- 9.
- 10.
- 11. カーブフィッティング 抵抗値の測定 1 2 … 18 19 2 4 … 36 38
- 12.
- 13.
- 14.
- 15. カーブフィッティング1 2 … 18 19 2 4 … 36 38
- 16.
- 17.
- 18. カーブフィッティング データ点を必ず通るので，正確？？ 明らかに間違った結果である 何が起きているのか？
- 19.
- 20. オーバーフィッティング 誤差（ノイズ）に敏感に反応 原因として考えられること 多項式の次数が大きすぎる 係数の要素が大きすぎる
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
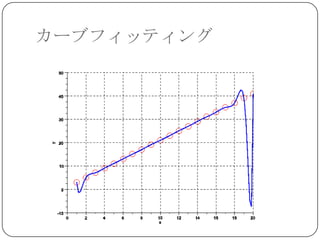
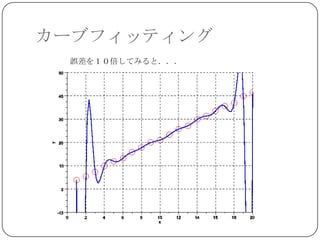
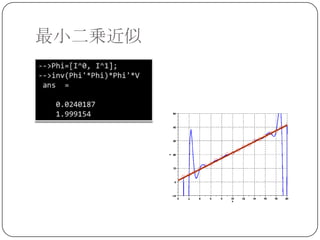
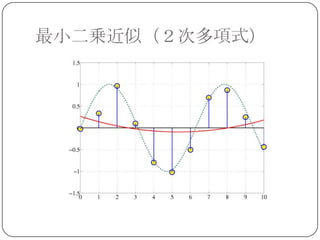
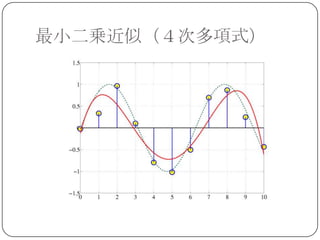
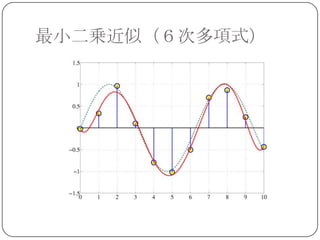
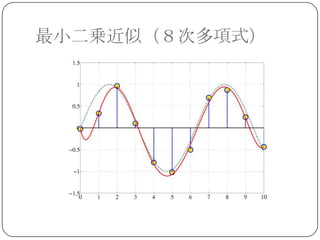
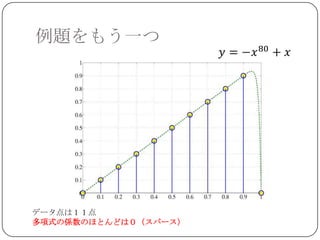
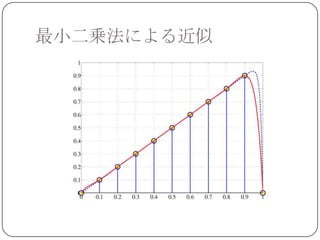
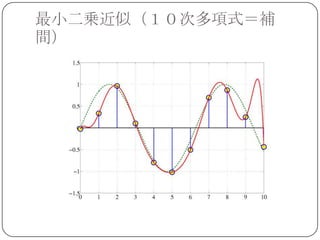
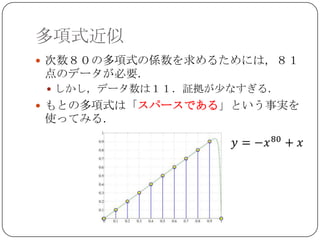
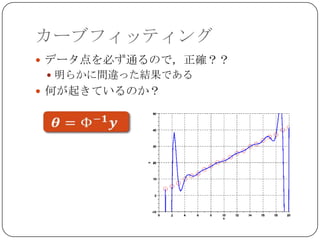
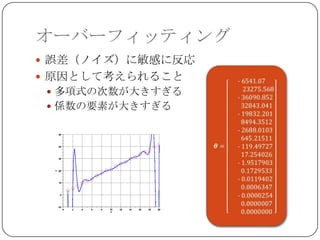
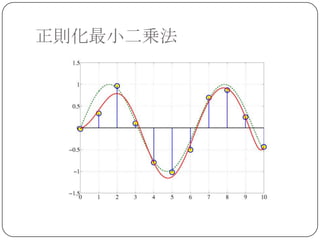
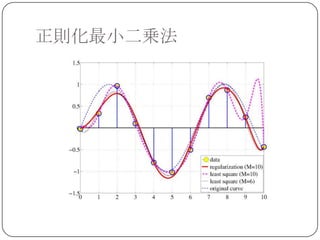
- 30. 最小二乗近似 上の例題では 6～ 8 次の多項式近似が比較的良 い結果を与える． データから自動的に多項式の次数を決めることは できないか？ 10次多項式の係数 6次多項式の係数 単純に係数の「大きさ」を小さくすれば 良くなりそう．．．
- 31. 正則化最小二乗法 誤差を小さくする
- 32.
- 33.
- 34. これまでのまとめ 最小ノルム解 最小２乗近似解
- 35.
- 36. 多項式近似 次数８０の多項式の係数を求めるためには，８１ 点のデータが必要． しかし，データ数は１１．証拠が少なすぎる． もとの多項式は「スパースである」という事実を 使ってみる．
- 37.
- 38. 「スパース」という情報を入れた場 合 Welcometo Sparse Land!
- 39. もくじ 連立方程式の復習 最小ノルム解 最小二乗近似解 正則化最小二乗法 Sparse Land での正則化最小二乗法 圧縮センシングの基礎 ネットワーク化制御への応用 まとめ
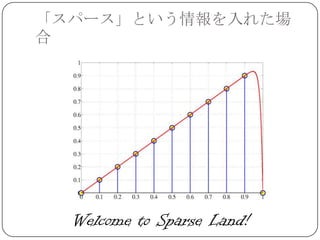
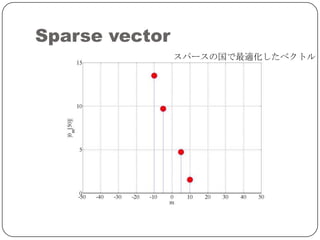
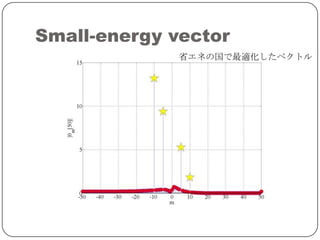
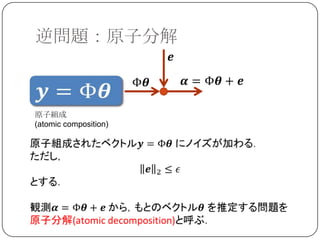
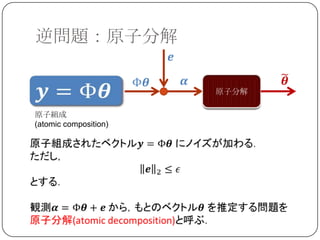
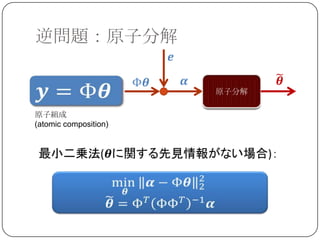
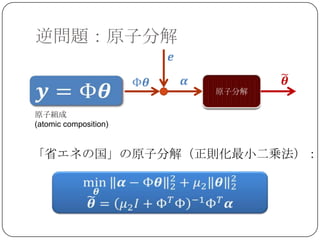
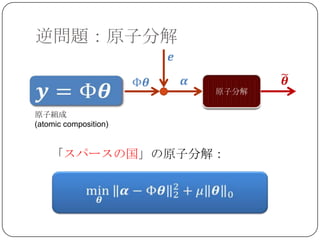
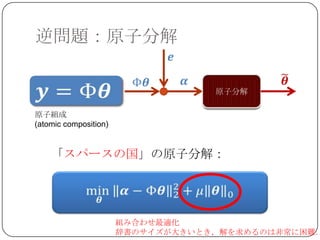
- 40. Sparse Land SparseLand＝スパースな信号の属する集合 圧縮センシング，圧縮サンプリング，スパース表 現など，最近話題のトピックの基礎となる． ここでは，Sparse Land とは何かを簡単に説明す る．
- 41. Sparse Land スパースの国に属するベクトル 0の数が多い “省エネの国”に属するベクトル エネルギー（L2ノルム）が小さい
- 42. Sparse vector スパースの国で最適化したベクトル
- 43. Small-energy vector 省エネの国で最適化したベクトル
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52. 逆問題：原子分解 原子組成 (atomic composition) 「スパースの国」の原子分解：
- 53. 逆問題：原子分解 原子組成 (atomic composition) 「スパースの国」の原子分解： 組み合わせ最適化 辞書のサイズが大きいとき，解を求めるのは非常に困難．
- 55. 逆問題：原子分解 原子組成 (atomic composition) 「スパースの国」の原子分解：
- 56.
- 57. もくじ 連立方程式の復習 最小ノルム解 最小二乗近似解 正則化最小二乗法 Sparse Land での正則化最小二乗法 圧縮センシングの基礎 ネットワーク化制御への応用 まとめ
- 58. ネットワーク化制御系 制御対象 コントローラ
- 59. ネットワーク化制御系 制御対象 コントローラ 制御対象とコントローラとの間の通信には制約が ある
- 60.
- 61. ネットワーク化制御 通信路制約のもとで，いかにうまく制御対象を 制御できるか？ 通信路制約 ビットレート制約 通信遅れ パケットロス etc 制御性能をなるべく崩さずに（少しは犠牲にし て），送信信号を効率よく圧縮したい． →スパースの国 (Sparse Land) へ！
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
- 71.
- 73. 高速アルゴリズム
- 74.
- 75.
- 76.
- 80.
- 81.