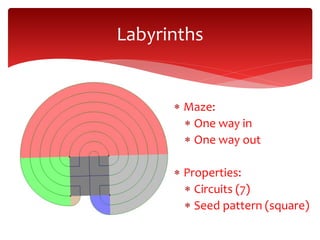
This document discusses the mathematics behind labyrinths. It begins by defining labyrinths and mazes, and provides examples of historical and contemporary labyrinths around the world. It then explains how classical labyrinths are constructed using a compass and straightedge by starting with a square and dilating points to form concentric circuits. The document analyzes various mathematical properties of labyrinths, such as the relationship between the number of circuits and other features. It presents labyrinth examples with different numbers of circuits. In conclusion, labyrinth construction and analysis provides opportunities to explore mathematical concepts.

1. The Mathematics of Labyrinths
David Thompson & Diana Cheng
Towson University

2.  Definition & example
Labyrinths
 Maze:
 One way in
 One way out
 Properties:
 Circuits (7)
 Seed pattern (square)

3. Greek mythology: Theseus entered a labyrinth & killed the Minotaur
Labyrinths around the world
Cathedrale Notre Dame de
Chartres, France (medieval)
Hopi Indians’
penta-seed pattern
(classical)
4000 year old concept

4. Labyrinths in architecture & art
Serpentine mosaic labyrinth in
Paphos, Cyprus (Roman)
Kabala or “Tree of Life”
labyrinth (classical)

5. Contemporary labyrinths
Tim Chartier’s (2014) Math Bytes labyrinths

6.  http://labyrinthlocator.com/home
 Baltimore area:
 JHU Bayview
 St John’s Lutheran Church (Parkville)
 Stevenson University’s Greenspring Campus -
Menning Meditation Center and Labyrinth
Find a labyrinth near you!

7.  Compass & straightedge
 GSP SP
Construction of Classical Labyrinths

8. 1. Construct a Square
2. Construct the midpoints & connect
opposite midpoints

9. From Each Midpoint to the end point
of the square dilate each point by a ½
ratio

10. Create a Cross and find the center of
the labyrinth

11. Using the center of the labyrinth
construct an arc on circle extend
points as necessary(arc on circle)

12. Create the quarter circles to
complete the circuits (arc through 3
points)

13. Construct the lower quarter circles
(Extend the lower part of the square arc through 3 points)
Hide all points except corners of square

14. Color the labyrinth using the exterior arcs
(semi circle, 2 upper and 2 lower quarter
cirlces) and square

15.  # of circuits and:
 # of dilated points in inner square
 # of interior intersection dots
 Radius & length of outer semi-circle radius
 Arc length & # circuits
 Area of labyrinth
 Dilations
 Equations of semi-circles
Math within labyrinths

16. 3 & 7 Circuit Labyrinths

17. 11 & 15 Circuit Labyrinths

18. 19 & 23 Circuit Labyrinths

19. # circuits vs. # dilated points

20. # circuits vs. # interior intersection dots

21. Radius vs.
Length of outer semi-circle radius

22. Arc length vs. # circuits

23. Area of labyrinth

24. Dilations

25. Equations of semi-circles

26. Equations of semi-circles (part 2)