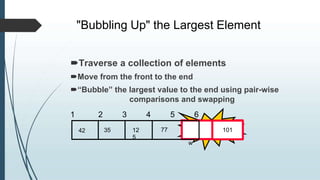
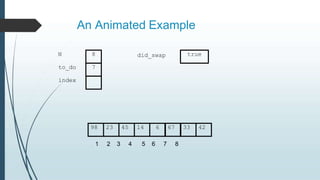
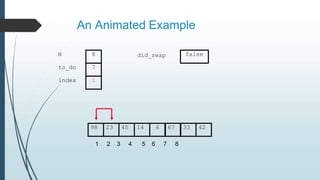
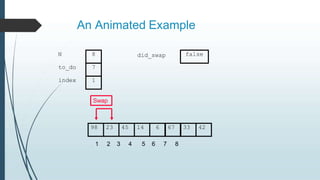
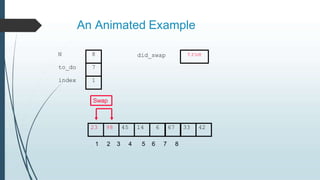
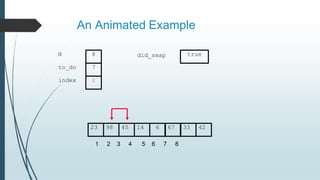
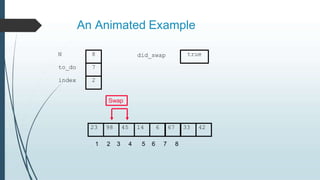
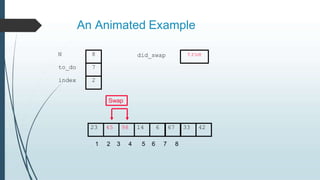
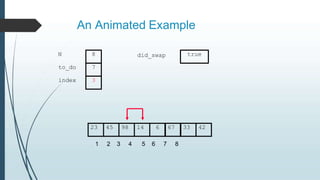
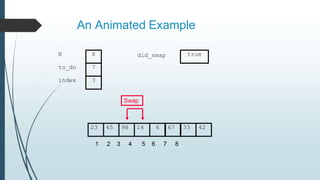
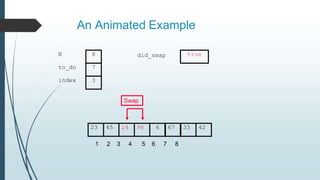
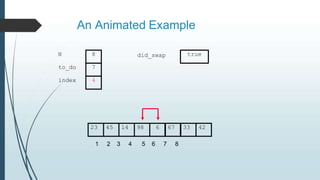
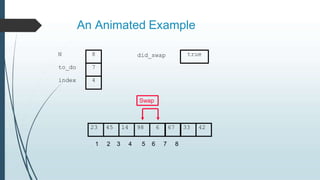
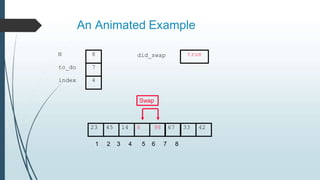
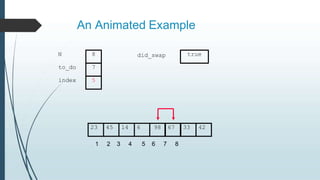
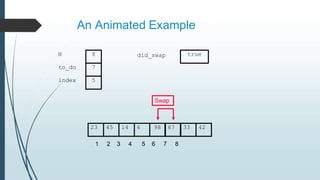
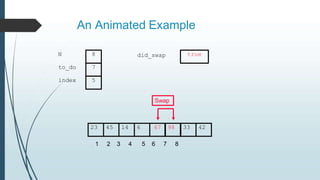
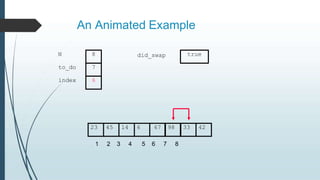
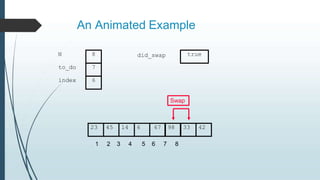
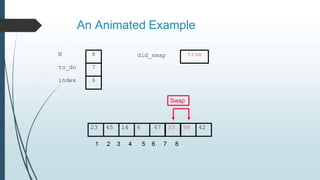
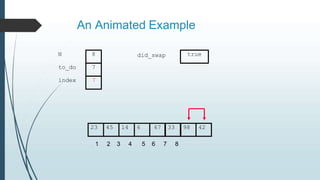
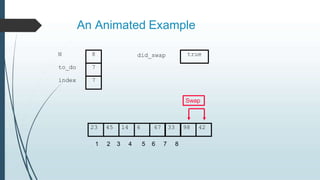
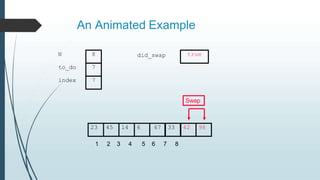
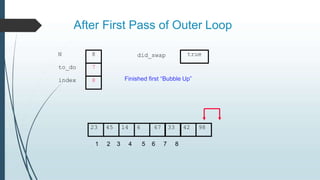
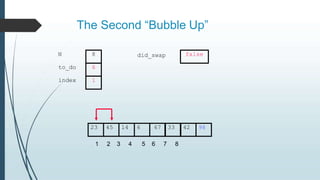
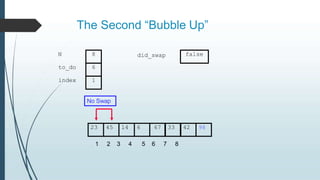
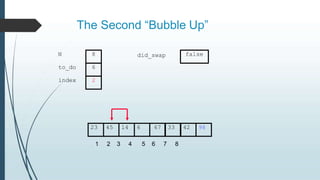
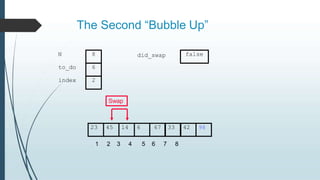
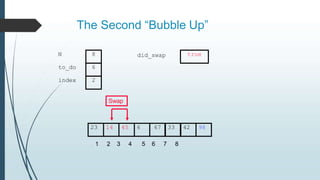
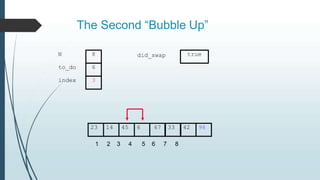
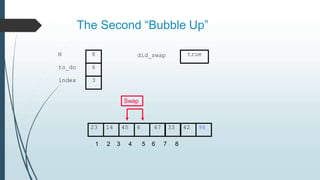
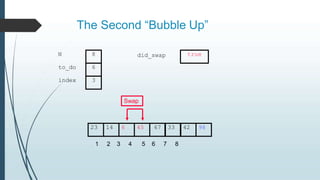
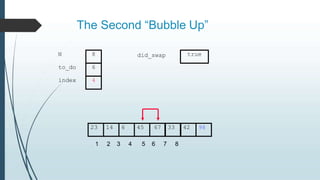
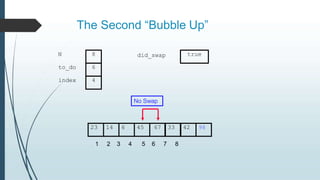
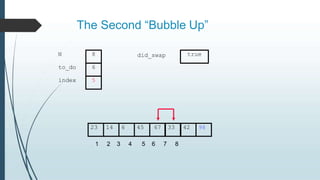
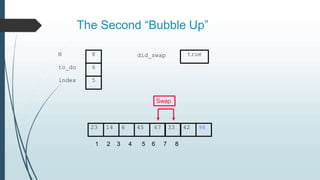
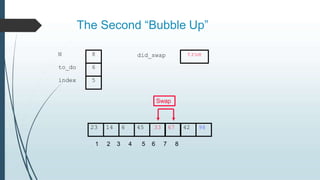
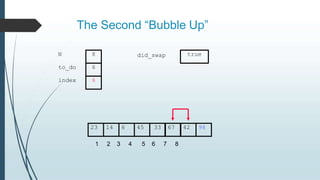
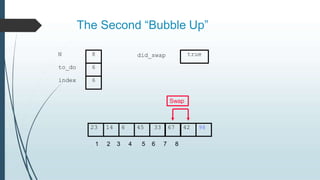
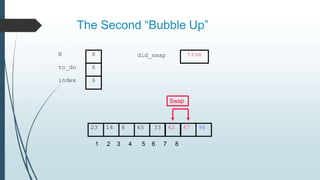
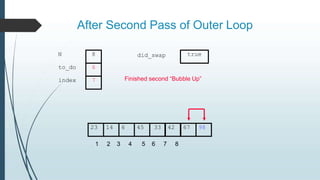
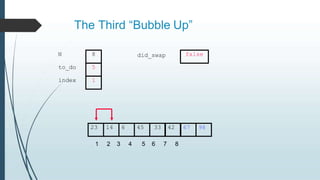
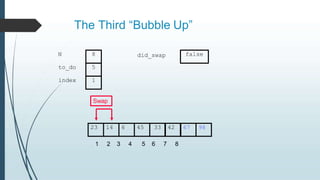
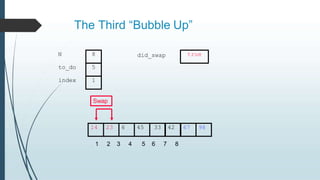
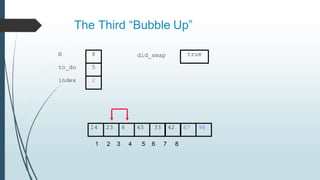
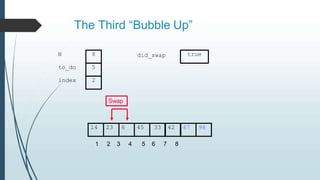
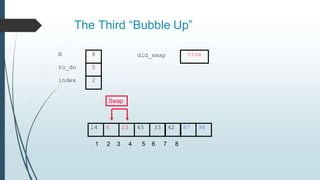
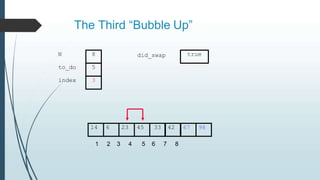
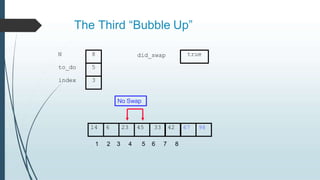
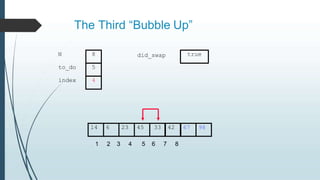
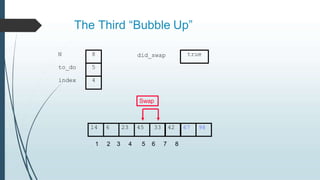
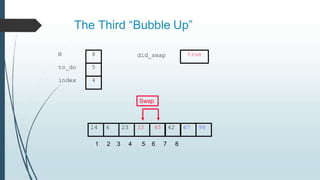
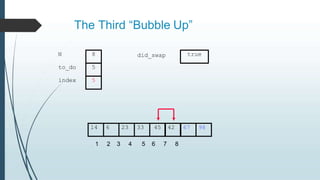
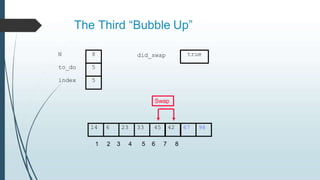
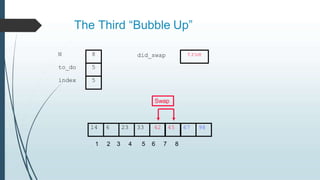
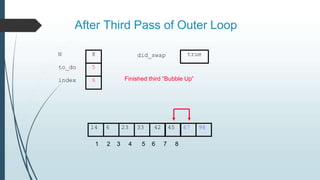
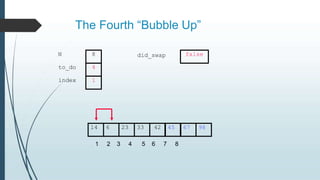
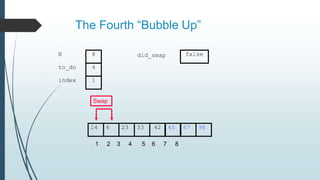
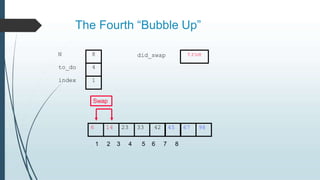
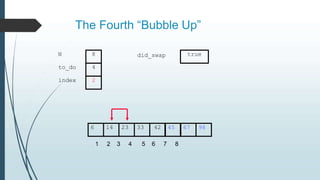
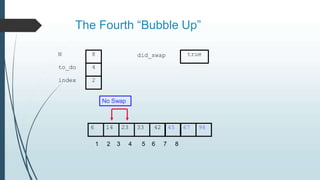
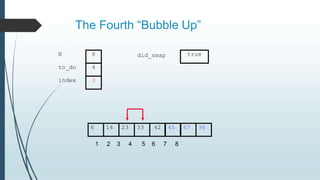
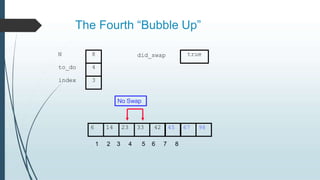
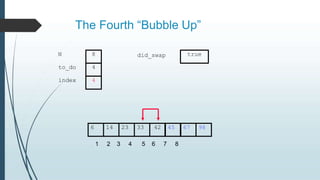
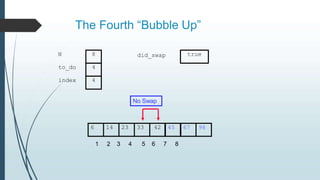
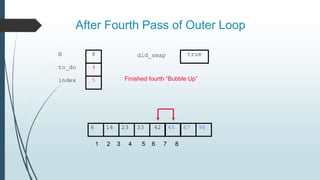
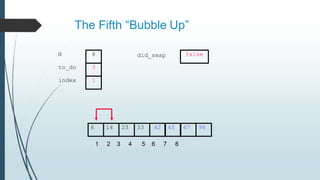
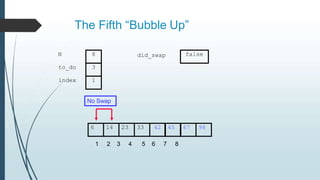
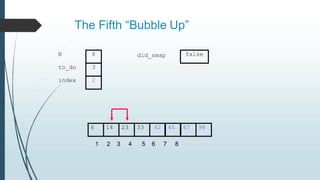
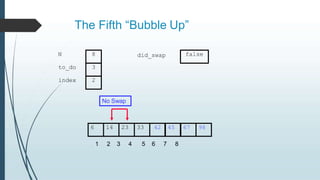
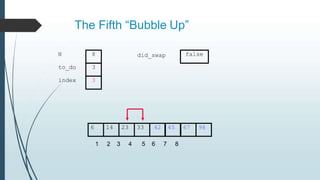
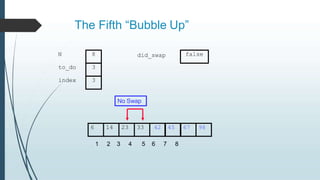
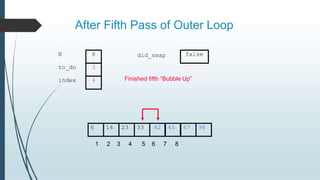
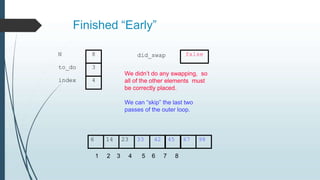
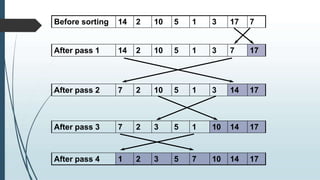
The document discusses sorting algorithms, specifically bubble sort. It provides an overview of sorting, why it is important, and common sorting algorithms like bubble sort, selection sort, and insertion sort. It then goes into detail on how bubble sort works, providing pseudocode and examples to show how it iteratively "bubbles up" the largest values to the end of the array after each pass through the elements.

1. C-Programming
----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
---------
-------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
Sorting

2. TOPICS TO BE COVERED
 Introduction to Sorting
 Bubble Sort
 Selection Sort
 Insertion Sort

3. Sortin
g

4. Sorting…
…
A fundamental application for computers
Done to make finding data (searching) faster
Many different algorithms for sorting
One of the difficulties with sorting is working with a fixed
size storage container (array)
if resize, that is expensive (slow)
The "simple" sorts run in quadratic time O(N2)
bubble sort
selection sort
insertion sort
4

5. Sorting…
…
To arrange a set of items in sequence.
It is estimated that 25~50% of all
computing power is used for sorting
activities.
Possible reasons:
Many applications require sorting;
Many applications perform sorting when they
don't have to;
Many applications use inefficient sorting
algorithms.

6. Sorting
Applications
To prepare a list of student ID, names, and
scores in a table (sorted by ID or name) for
easy checking.
To prepare a list of scores before letter grade
assignment.
To produce a list of horses after a race (sorted
by the finishing times) for payoff calculation.
To prepare an originally unsorted array for
ordered binary searching.

7. Bubble
Sort

8. Bubble
Sort……
Bubble sort examines the array from start to finish,
comparing elements as it goes.
Any time it finds a larger element before a smaller
element, it swaps the two.
In this way, the larger elements are passed towards the
end.
The largest element of the array therefore "bubbles" to
the end of the array.
Then it repeats the process for the unsorted portion of the
array until the whole array is sorted.

9. Bubble
Sort……
Bubble sort works on the same general principle
as shaking a soft drink bottle.
Right after shaking, the contents are a mixture of
bubbles and soft drink, distributed randomly.
Because bubbles are lighter than the soft drink,
they rise to the surface, displacing the soft drink
downwards.
This is how bubble sort got its name, because the
smaller elements "float" to the top, while
the larger elements "sink" to the bottom.

10. "Bubbling Up" the Largest Element
77 42 35 12 101 5
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6

11. "Bubbling Up" the Largest Element
5
12 101
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6
77
S
w
ap
42
42 77 35

12. "Bubbling Up" the Largest Element
5
12 101
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6
77
S
w
ap35
42 35 77

13. "Bubbling Up" the Largest Element
42 101
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6
77
S
w
ap12
35 12 77 5

14. "Bubbling Up" the Largest Element
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6
42 35 12 77 101 5
No need to swap

15. "Bubbling Up" the Largest Element
35
42
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6
101
S
w
ap 5
12 77
5
101

16. "Bubbling Up" the Largest Element
Traverse a collection of elements
Move from the front to the end
“Bubble” the largest value to the end using pair-wise
comparisons and swapping
1 2 3 4 5 6
42 35 12 77 5 101
Largest value correctly placed

17. An Animated Example
98 23 45 14 6 67 33 42
to_do
index
7
N
1 2 3 4 5 6 7 8
8 did_swap true

18. An Animated Example
98 23 45 14 6 67 33 42
to_do
index
7
1
N 8 did_swap
1 2 3 4 5 6 7 8
false

19. An Animated Example
98 23 45 14 6 67 33 42
to_do
index
7
1
N 8
Swap
1 2 3 4 5 6 7 8
did_swap false

20. An Animated Example
23 98 45 14 6 67 33 42
to_do
index
7
1
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

21. An Animated Example
23 98 45 14 6 67 33 42
to_do
index
7
2
N 8 did_swap
1 2 3 4 5 6 7 8
true

22. An Animated Example
23 98 45 14 6 67 33 42
to_do
index
7
2
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

23. An Animated Example
23 45 98 14 6 67 33 42
to_do
index
7
2
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

24. An Animated Example
23 45 98 14 6 67 33 42
to_do
index
7
3
N 8 did_swap
1 2 3 4 5 6 7 8
true

25. An Animated Example
23 45 98 14 6 67 33 42
to_do
index
7
3
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

26. An Animated Example
23 45 14 98 6 67 33 42
to_do
index
7
3
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

27. An Animated Example
23 45 14 98 6 67 33 42
to_do
index
7
4
N 8 did_swap
1 2 3 4 5 6 7 8
true

28. An Animated Example
23 45 14 98 6 67 33 42
to_do
index
7
4
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

29. An Animated Example
23 45 14 6 98 67 33 42
to_do
index
7
4
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

30. An Animated Example
23 45 14 6 98 67 33 42
to_do
index
7
5
N 8 did_swap
1 2 3 4 5 6 7 8
true

31. An Animated Example
23 45 14 6 98 67 33 42
to_do
index
7
5
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

32. An Animated Example
23 45 14 6 67 98 33 42
to_do
index
7
5
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

33. An Animated Example
23 45 14 6 67 98 33 42
to_do
index
7
6
N 8 did_swap
1 2 3 4 5 6 7 8
true

34. An Animated Example
23 45 14 6 67 98 33 42
to_do
index
7
6
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

35. An Animated Example
23 45 14 6 67 33 98 42
to_do
index
7
6
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

36. An Animated Example
23 45 14 6 67 33 98 42
to_do
index
7
7
N 8 did_swap
1 2 3 4 5 6 7 8
true

37. An Animated Example
23 45 14 6 67 33 98 42
to_do
index
7
7
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

38. An Animated Example
23 45 14 6 67 33 42 98
to_do
index
7
7
N 8
Swap
1 2 3 4 5 6 7 8
did_swap true

39. After First Pass of Outer Loop
23 45 14 6 67 33 42 98
to_do
index
7
8
N 8
Finished first “Bubble Up”
1 2 3 4 5 6 7 8
did_swap true

40. The Second “Bubble Up”
23 45 14 6 67 33 42 98
to_do
index
6
1
N 8 did_swap
1 2 3 4 5 6 7 8
false

41. The Second “Bubble Up”
23 45 14 6 67 33 42 98
to_do
index
6
1
N 8 did_swap
1 2 3 4 5 6 7 8
false
No Swap

42. The Second “Bubble Up”
23 45 14 6 67 33 42 98
to_do
index
6
2
N 8 did_swap
1 2 3 4 5 6 7 8
false

43. The Second “Bubble Up”
23 45 14 6 67 33 42 98
to_do
index
6
2
N 8 did_swap
1 2 3 4 5 6 7 8
false
Swap

44. The Second “Bubble Up”
23 14 45 6 67 33 42 98
to_do
index
6
2
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

45. The Second “Bubble Up”
23 14 45 6 67 33 42 98
to_do
index
6
3
N 8 did_swap
1 2 3 4 5 6 7 8
true

46. The Second “Bubble Up”
23 14 45 6 67 33 42 98
to_do
index
6
3
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

47. The Second “Bubble Up”
23 14 6 45 67 33 42 98
to_do
index
6
3
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

48. The Second “Bubble Up”
23 14 6 45 67 33 42 98
to_do
index
6
4
N 8 did_swap
1 2 3 4 5 6 7 8
true

49. The Second “Bubble Up”
23 14 6 45 67 33 42 98
to_do
index
6
4
N 8 did_swap
1 2 3 4 5 6 7 8
true
No Swap

50. The Second “Bubble Up”
23 14 6 45 67 33 42 98
to_do
index
6
5
N 8 did_swap
1 2 3 4 5 6 7 8
true

51. The Second “Bubble Up”
23 14 6 45 67 33 42 98
to_do
index
6
5
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

52. The Second “Bubble Up”
23 14 6 45 33 67 42 98
to_do
index
6
5
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

53. The Second “Bubble Up”
23 14 6 45 33 67 42 98
to_do
index
6
6
N 8 did_swap
1 2 3 4 5 6 7 8
true

54. The Second “Bubble Up”
23 14 6 45 33 67 42 98
to_do
index
6
6
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

55. The Second “Bubble Up”
23 14 6 45 33 42 67 98
to_do
index
6
6
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

56. After Second Pass of Outer Loop
23 14 6 45 33 42 67 98
to_do
index
6
7
N 8 did_swap
1 2 3 4 5 6 7 8
true
Finished second “Bubble Up”

57. The Third “Bubble Up”
23 14 6 45 33 42 67 98
to_do
index
5
1
N 8 did_swap
1 2 3 4 5 6 7 8
false

58. The Third “Bubble Up”
23 14 6 45 33 42 67 98
to_do
index
5
1
N 8 did_swap
1 2 3 4 5 6 7 8
false
Swap

59. The Third “Bubble Up”
14 23 6 45 33 42 67 98
to_do
index
5
1
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

60. The Third “Bubble Up”
14 23 6 45 33 42 67 98
to_do
index
5
2
N 8 did_swap
1 2 3 4 5 6 7 8
true

61. The Third “Bubble Up”
14 23 6 45 33 42 67 98
to_do
index
5
2
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

62. The Third “Bubble Up”
14 6 23 45 33 42 67 98
to_do
index
5
2
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

63. The Third “Bubble Up”
14 6 23 45 33 42 67 98
to_do
index
5
3
N 8 did_swap
1 2 3 4 5 6 7 8
true

64. The Third “Bubble Up”
14 6 23 45 33 42 67 98
to_do
index
5
3
N 8 did_swap
1 2 3 4 5 6 7 8
true
No Swap

65. The Third “Bubble Up”
14 6 23 45 33 42 67 98
to_do
index
5
4
N 8 did_swap
1 2 3 4 5 6 7 8
true

66. The Third “Bubble Up”
14 6 23 45 33 42 67 98
to_do
index
5
4
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

67. The Third “Bubble Up”
14 6 23 33 45 42 67 98
to_do
index
5
4
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

68. The Third “Bubble Up”
14 6 23 33 45 42 67 98
to_do
index
5
5
N 8 did_swap
1 2 3 4 5 6 7 8
true

69. The Third “Bubble Up”
14 6 23 33 45 42 67 98
to_do
index
5
5
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

70. The Third “Bubble Up”
14 6 23 33 42 45 67 98
to_do
index
5
5
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

71. After Third Pass of Outer Loop
14 6 23 33 42 45 67 98
to_do
index
5
6
N 8 did_swap
1 2 3 4 5 6 7 8
true
Finished third “Bubble Up”

72. The Fourth “Bubble Up”
14 6 23 33 42 45 67 98
to_do
index
4
1
N 8 did_swap
1 2 3 4 5 6 7 8
false

73. The Fourth “Bubble Up”
14 6 23 33 42 45 67 98
to_do
index
4
1
N 8 did_swap
1 2 3 4 5 6 7 8
false
Swap

74. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
1
N 8 did_swap
1 2 3 4 5 6 7 8
true
Swap

75. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
2
N 8 did_swap
1 2 3 4 5 6 7 8
true

76. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
2
N 8 did_swap
1 2 3 4 5 6 7 8
true
No Swap

77. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
3
N 8 did_swap
1 2 3 4 5 6 7 8
true

78. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
3
N 8 did_swap
1 2 3 4 5 6 7 8
true
No Swap

79. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
4
N 8 did_swap
1 2 3 4 5 6 7 8
true

80. The Fourth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
4
4
N 8 did_swap
1 2 3 4 5 6 7 8
true
No Swap

81. After Fourth Pass of Outer Loop
6 14 23 33 42 45 67 98
to_do
index
4
5
N 8 did_swap
1 2 3 4 5 6 7 8
true
Finished fourth “Bubble Up”

82. The Fifth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
3
1
N 8 did_swap
1 2 3 4 5 6 7 8
false

83. The Fifth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
3
1
N 8 did_swap
1 2 3 4 5 6 7 8
false
No Swap

84. The Fifth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
3
2
N 8 did_swap
1 2 3 4 5 6 7 8
false

85. The Fifth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
3
2
N 8 did_swap
1 2 3 4 5 6 7 8
false
No Swap

86. The Fifth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
3
3
N 8 did_swap
1 2 3 4 5 6 7 8
false

87. The Fifth “Bubble Up”
6 14 23 33 42 45 67 98
to_do
index
3
3
N 8 did_swap
1 2 3 4 5 6 7 8
false
No Swap

88. After Fifth Pass of Outer Loop
6 14 23 33 42 45 67 98
to_do
index
3
4
N 8 did_swap
1 2 3 4 5 6 7 8
false
Finished fifth “Bubble Up”

89. Finished “Early”
1 2 3 4 5 6 7 8
6 14 23 33 42 45 67 98
to_do
index
3
4
N 8 did_swap false
We didn’t do any swapping, so
all of the other elements must
be correctly placed.
We can “skip” the last two
passes of the outer loop.

90. Example:
#include <stdio.h>
void bubble_sort(long [], long); int main()
{
long array[100], n, c, d, swap; printf("Enter
number of elements:"); scanf("%ld", &n);
printf("Enter %ld longegersn", n); for (c = 0; c
< n; c++)
scanf("%ld", &array[c]);
bubble_sort(array, n);
printf("Sorted list in ascending order:n"); for (
c = 0 ; c < n ; c++ )
printf("%ldn", array[c]);
return 0;
}

91. void bubble_sort(long list[], long n)
{
long c, d, t;
for (c = 0 ; c < ( n - 1 ); c++)
{
for (d = 0 ; d < n - c - 1; d++)
{
if (list[d] > list[d+1])
{
t = list[d];
list[d] = list[d+1]; list[d+1]= t;
}
}
}
}

92. Selection
Sort……

93. Selection
Sort……
Idea:
Find the largest element in the array
Exchange it with the element in the
rightmost position
Find the second largest element and
exchange it with the element in the second
rightmost position
Continue until the array is sorted

94. Before sorting 14 2 10 5 1 3 17 7
After pass 1 14 2 10 5 1 3 7 17
After pass 2 7 2 10 5 1 3 14 17
After pass 3 7 2 3 5 1 10 14 17
After pass 4 1 2 3 5 7 10 14 17

95. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

96. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

97. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

98. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

99. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

100. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

101. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

102. Selection Sort
5 1 3 4 6 2
Comparison
Data Movement
Sorted

Largest

103. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

104. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

105. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

106. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

107. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

108. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

109. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

110. Selection Sort
5 1 3 4 2 6
Comparison
Data Movement
Sorted

Largest

111. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

112. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

113. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

114. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

115. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

116. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

117. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

Largest

118. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

119. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

120. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

121. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

122. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

123. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

Largest

124. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

125. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

126. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

127. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

128. Selection Sort
2 1 3 4 5 6
Comparison
Data Movement
Sorted

Largest

129. Selection Sort
1 2 3 4 5 6
Comparison
Data Movement
Sorted

130. Selection Sort
1 2 3 4 5 6
Comparison
Data Movement
Sorted
DONE!

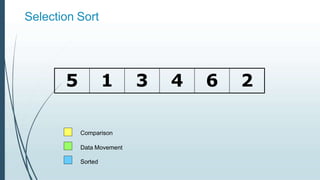
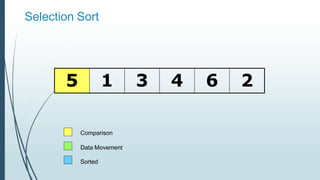
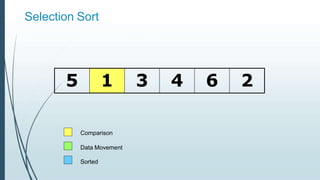
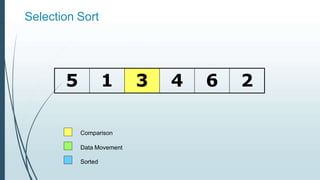
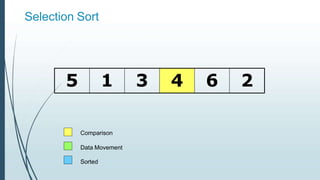
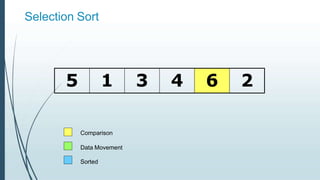
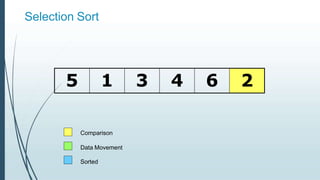
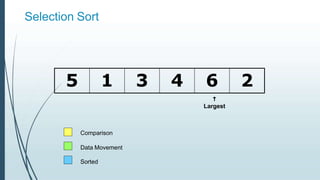
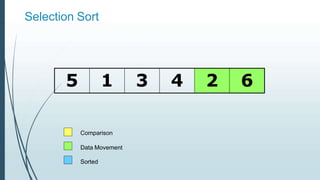
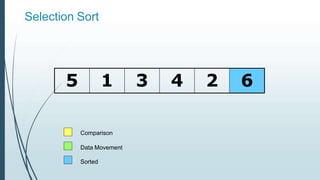
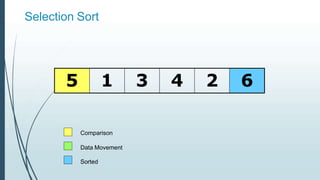
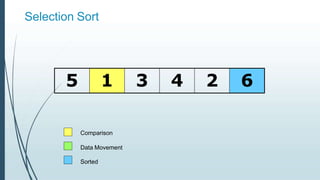
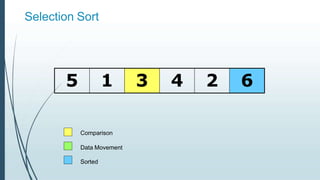
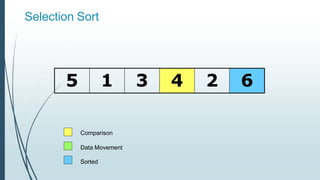
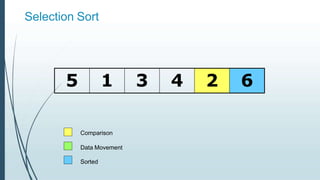
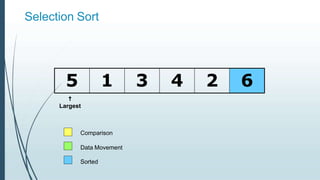
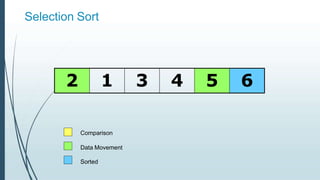
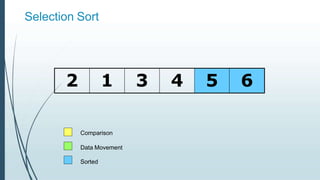
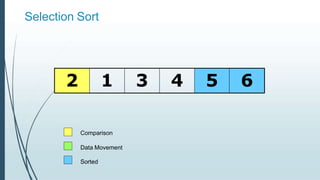
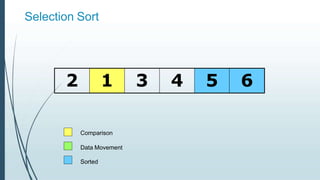
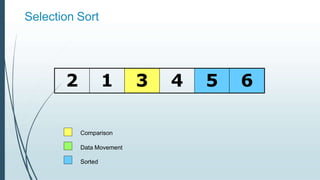
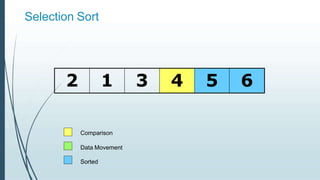
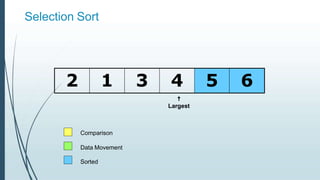
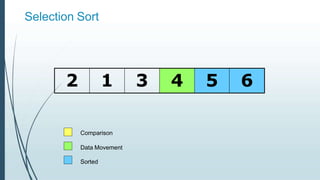
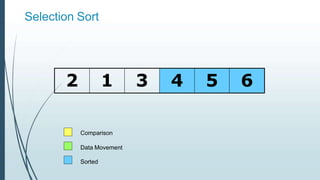
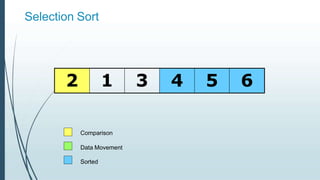
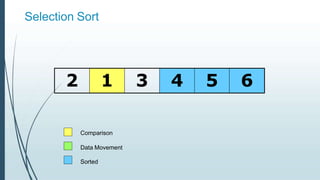
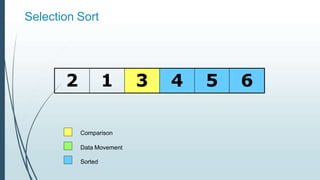
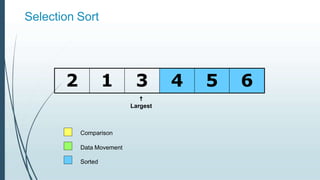
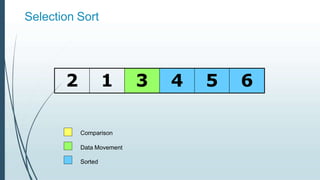
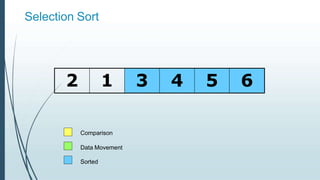
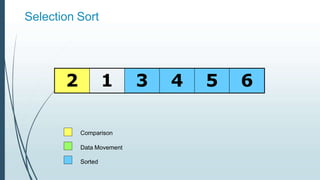
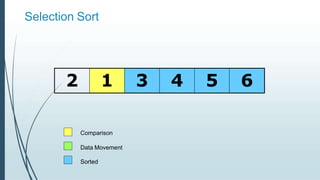
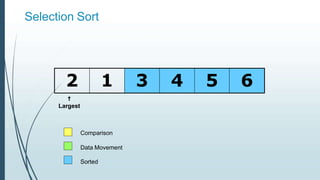
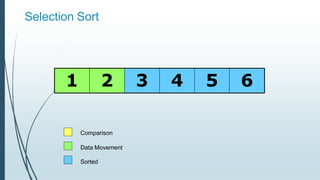
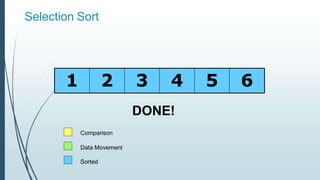
131. Example:
#include <stdio.h> main()
{
int A[20], N, Temp, i, j;
printf(" ENTER THE NUMBER OF TERMS...: ");
scanf("%d",&N);
printf("n ENTER THE ELEMENTS OF THE
ARRAY...:");
for(i=1; i<=N; i++)
{
scanf("ntt%d", &A[i]);
}

132. for(i=1; i<=N-1; i++) for(j=i+1; j<=N;j++)
if(A[i]>A[j])
{
Temp = A[i]; A[i] = A[j];
A[j] = Temp;
}
printf("THE ASCENDING ORDER LIST IS...:n");
for(i=1; i<=N; i++) printf("n %d",A[i]);
}

133. Insertion
Sort……

134. Insertion
Sort……
134
 Idea: like sorting a hand of playing cards
Start with an empty left hand and the cards facing
down on the table.
Remove one card at a time from the table, and insert it into
the correct position in the left hand
compare it with each of the cards already in the hand, from
right to left
The cards held in the left hand are sorted
these cards were originally the top cards of the pile on the
table

135. To insert 12, we need to
make room for it by
moving first 36 and then 24.
Insertion Sort
135

136. Insertion Sort
136

137. Insertion Sort
137

138. Insertion Sort
left sub-array
138
right sub-array
input array
5 2 4 6 1 3
at each iteration, the array is divided in two sub-arrays:
sorted unsorted

139. Insertion Sort
139

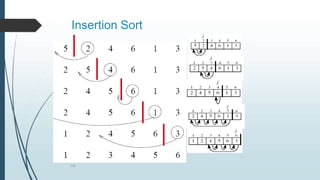
140. #include<stdio.h> void main()
{
int A[20], N, Temp, i, j;
printf("ENTER THE NUMBER OF TERMS...: ");
scanf("%d", &N);
printf("n ENTER THE ELEMENTS OF THE ARRAY...:");
for(i=0; i<N; i++)
{
scanf("ntt%d",&A[i]);
}
Example:

141. for(i=1; i<N; i++)
{
Temp = A[i];
j = i-1;
while(Temp<A[j] && j>=0)
{
A[j+1] = A[j];
j = j-1;
}
A[j+1] = Temp;
}
printf("nTHE ASCENDING ORDER LIST IS...:n");
for(i=0; i<N; i++) printf("n%d", A[i]);
}

142. THANK
YOU
FOR
LISTENIN