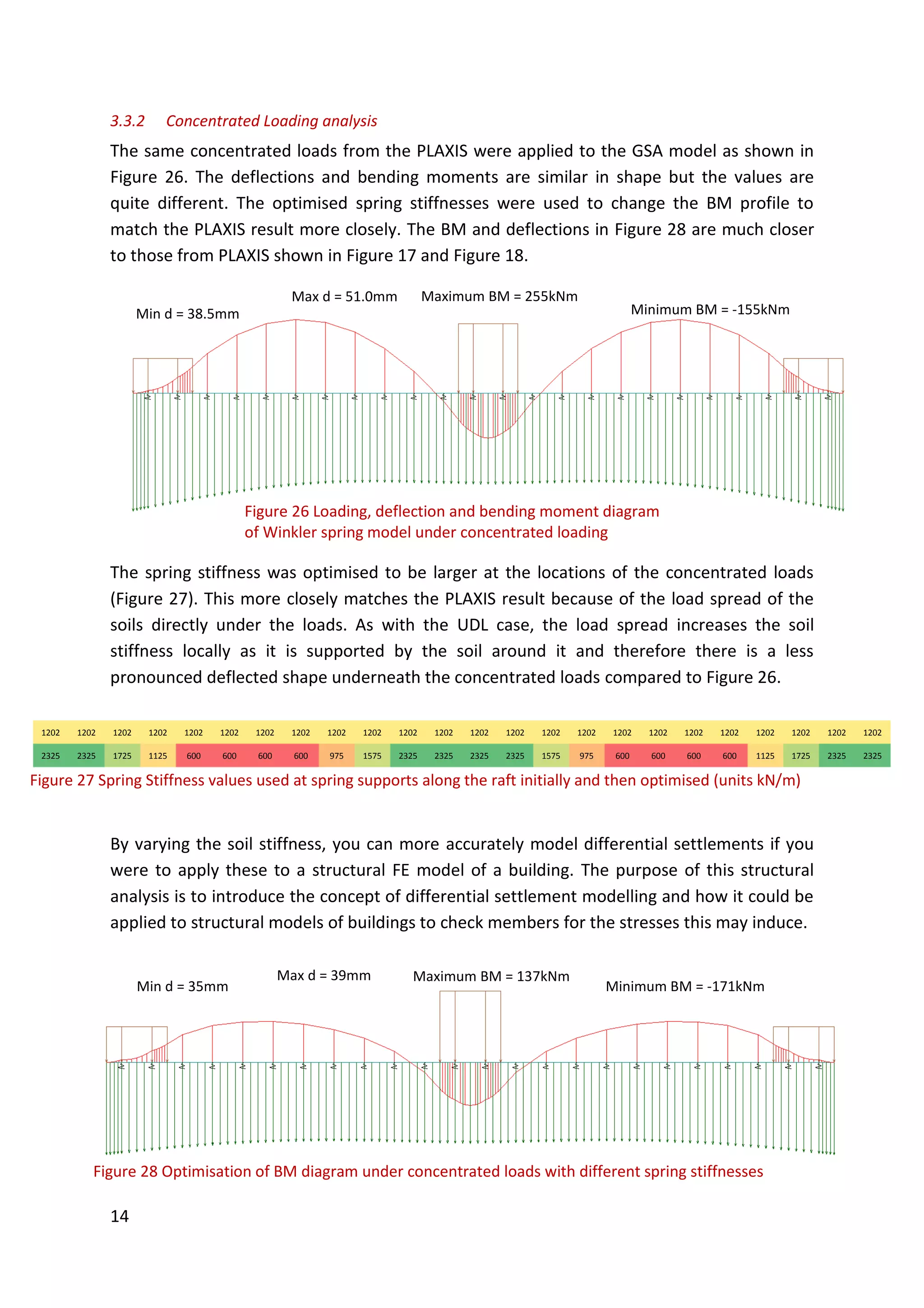
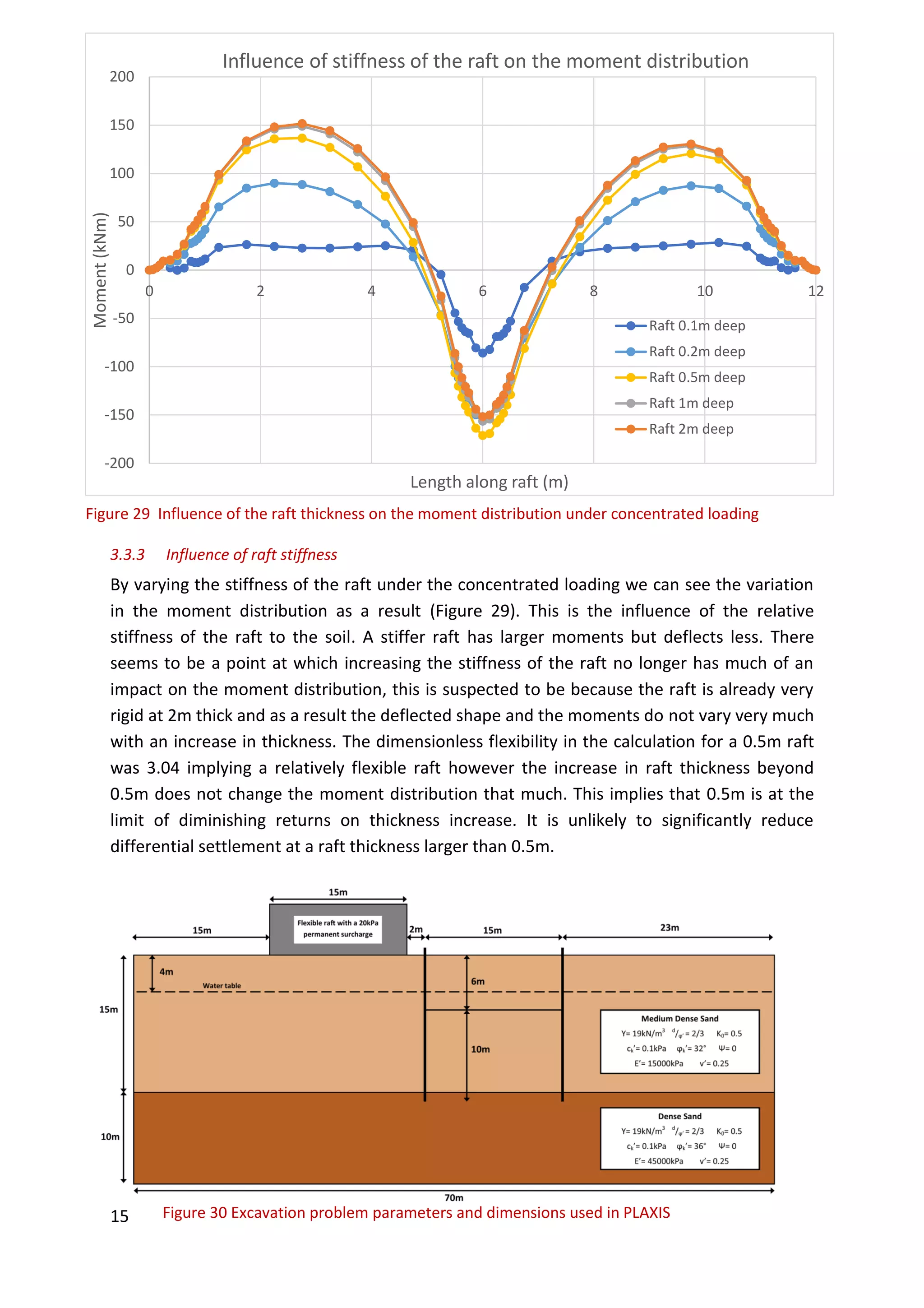
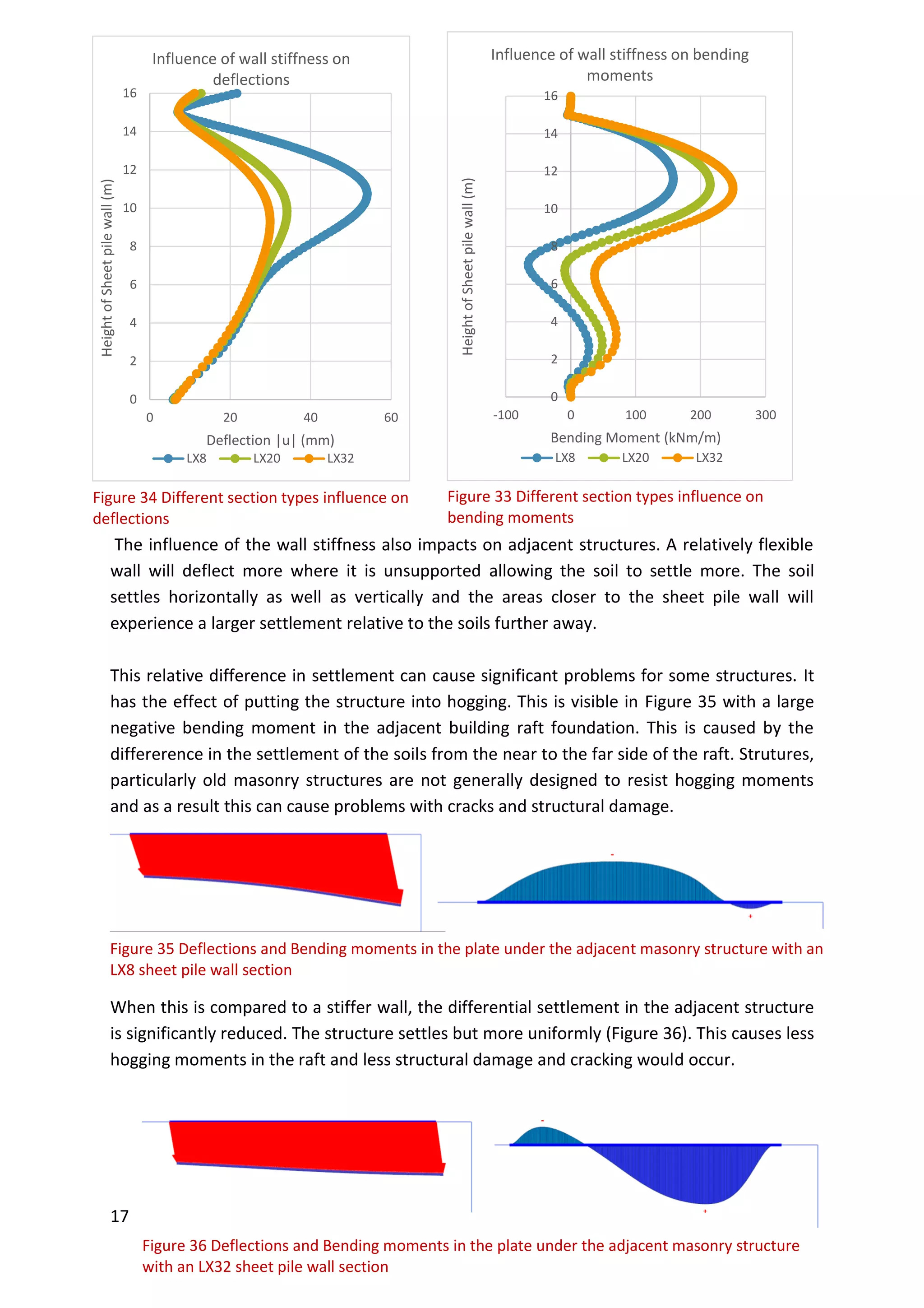
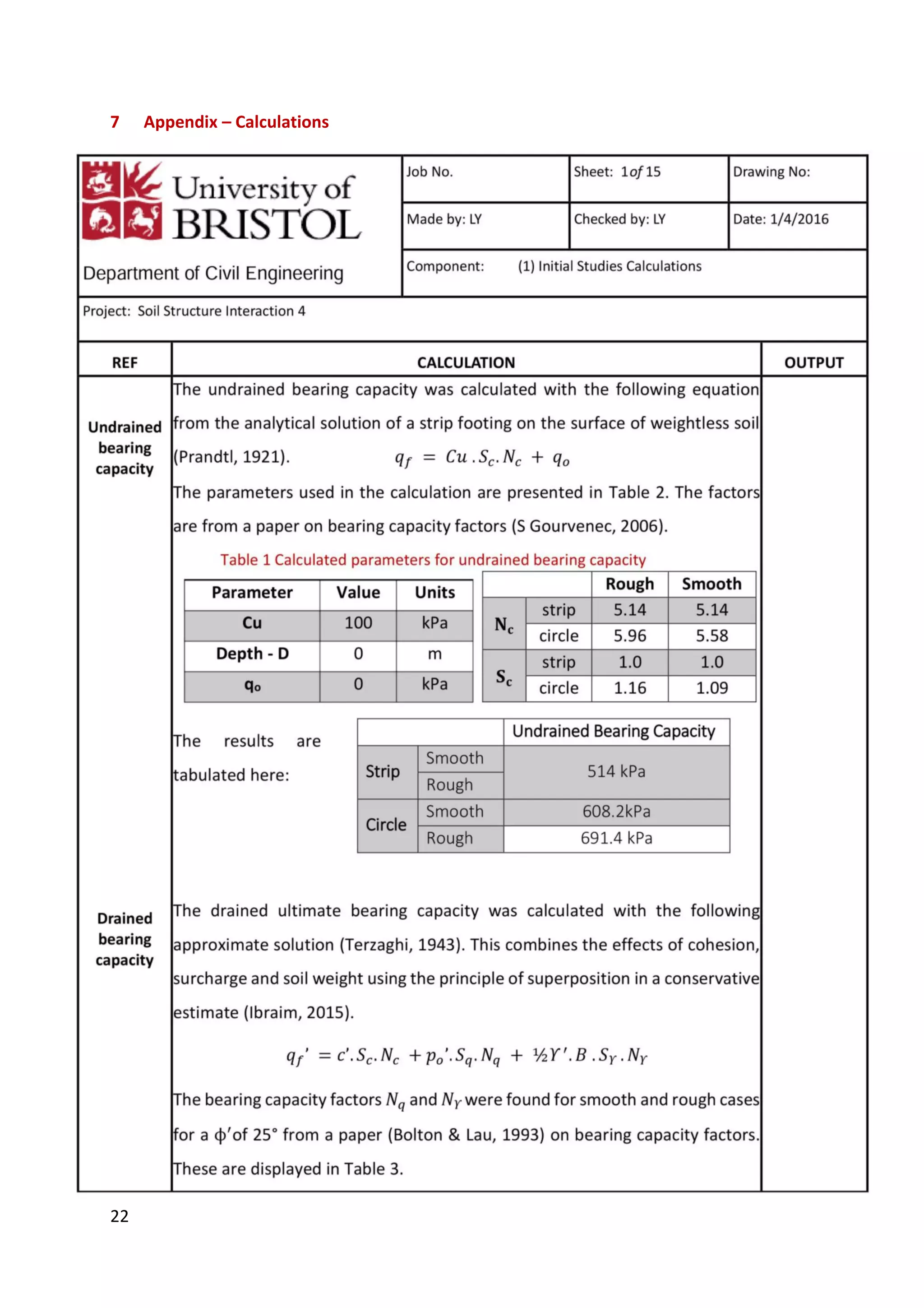
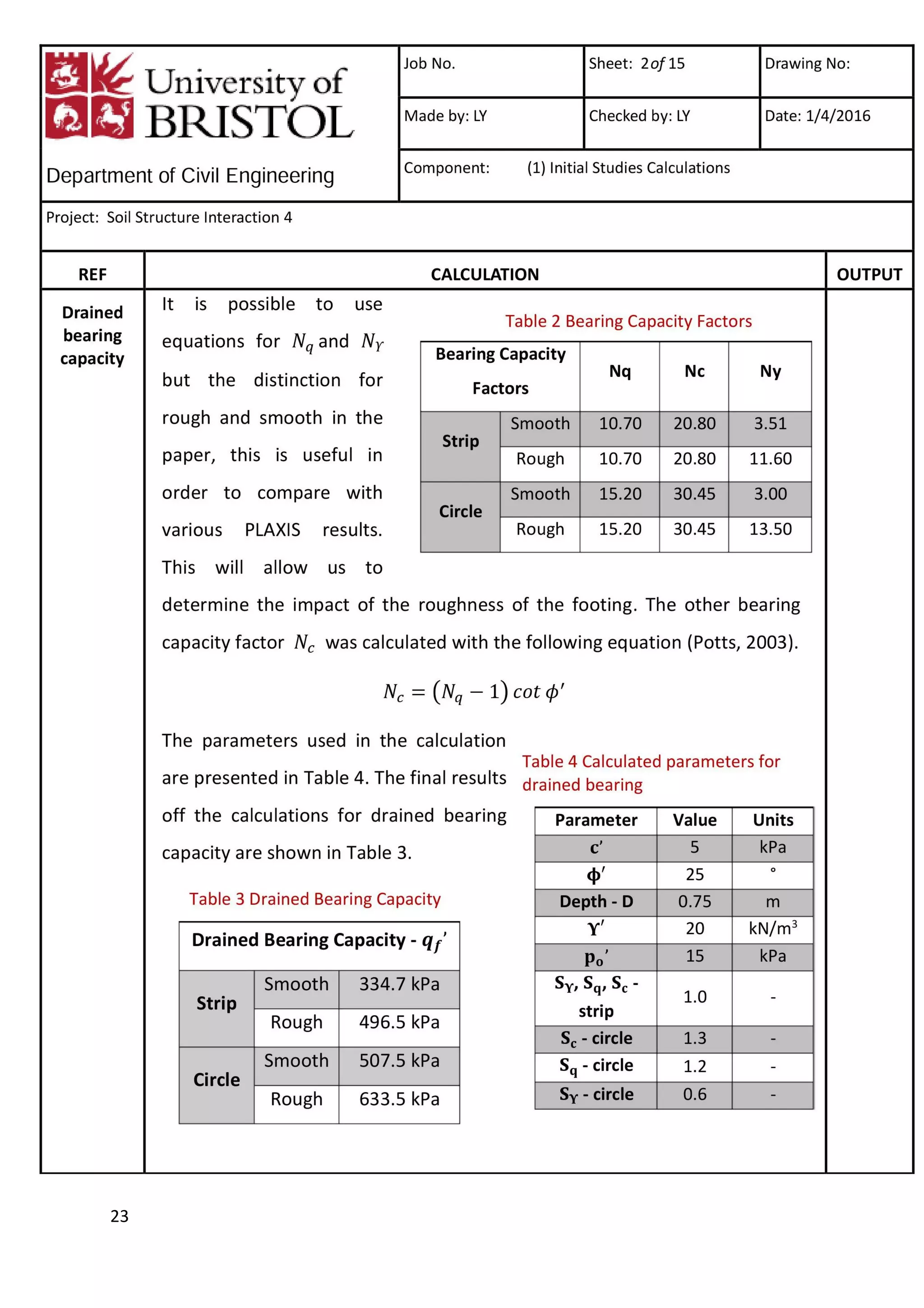
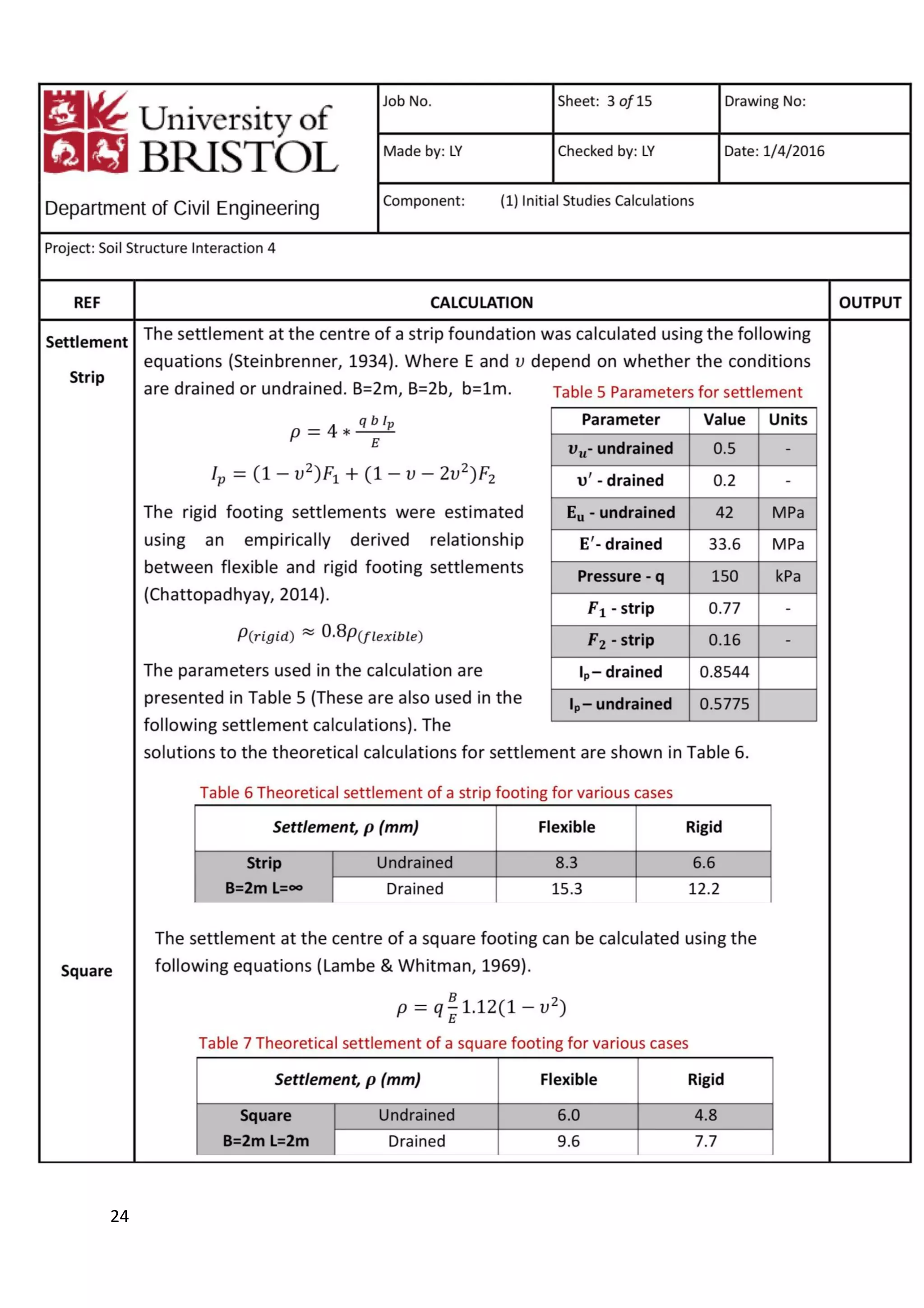
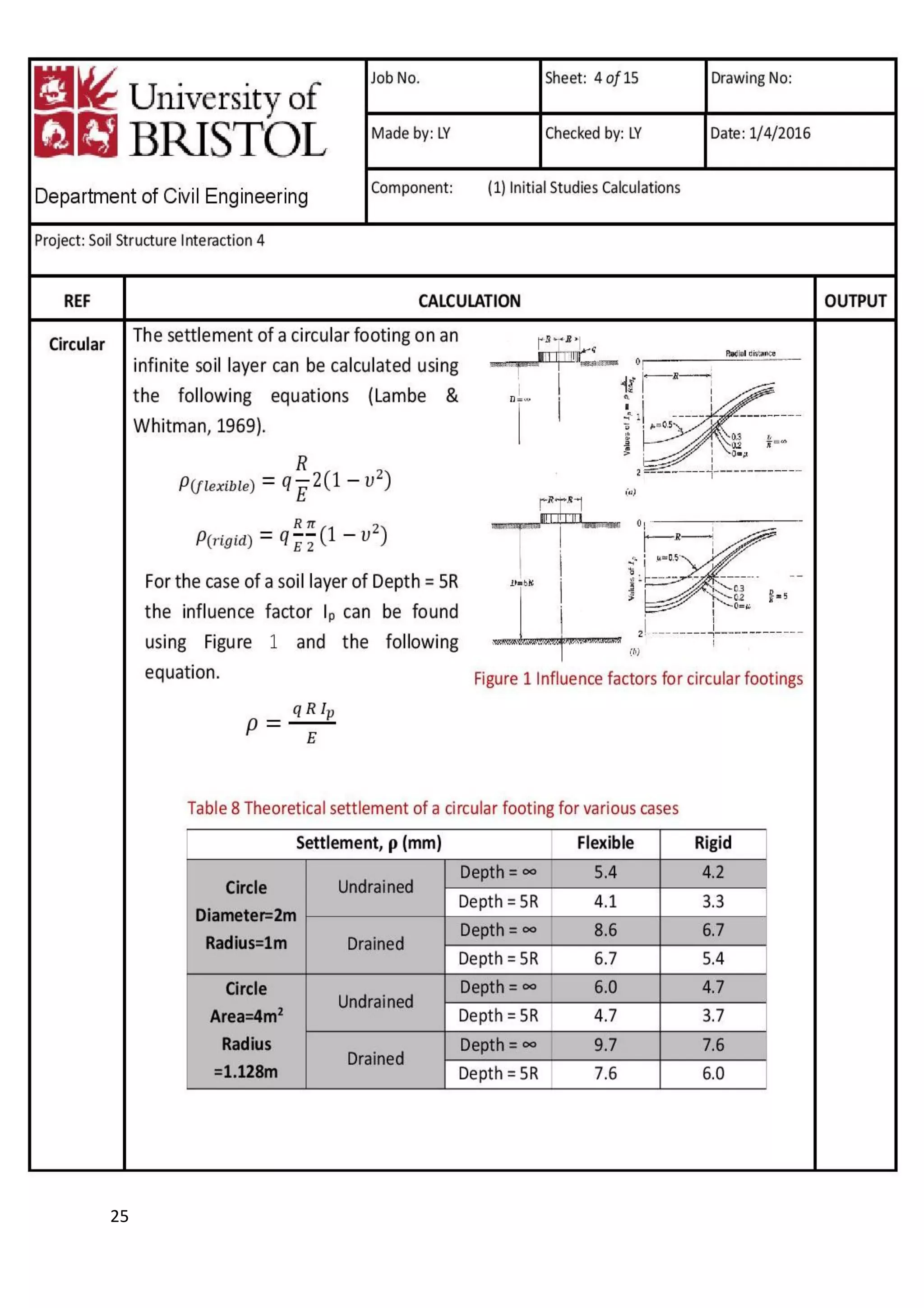
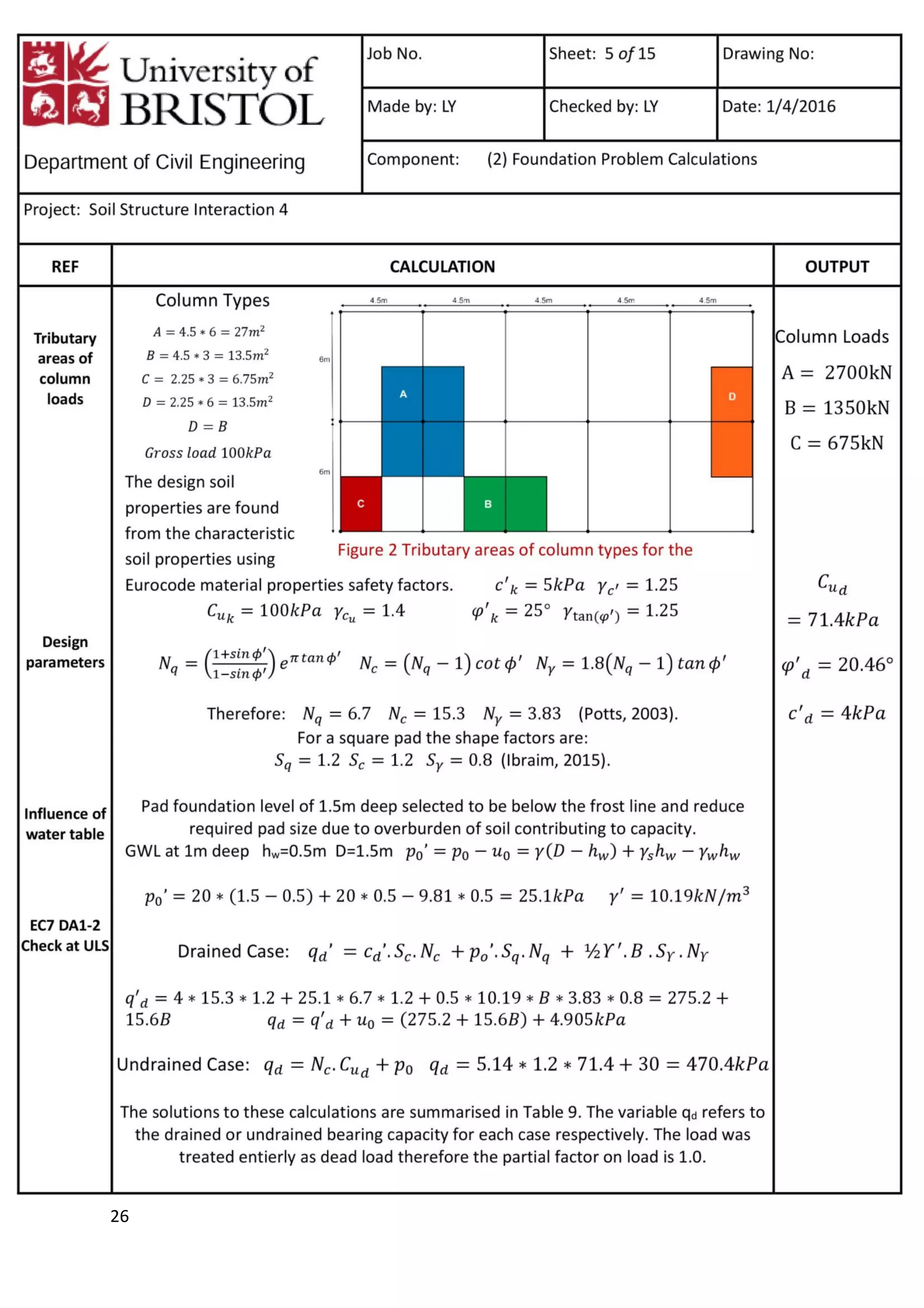
This document is a study report on using finite element modeling (PLAXIS) to analyze soil-structure interaction. The report contains initial studies comparing PLAXIS results to hand calculations on bearing capacity and settlement of foundations. Key findings from the initial studies include: 1) Mesh refinement near the footing improves accuracy more than general refinement; 2) Boundaries should be at least 1-2 times the footing width away; 3) PLAXIS predicts undrained capacity and settlement well but overestimates drained capacity. The report then analyzes a foundation problem and excavation problem in PLAXIS.