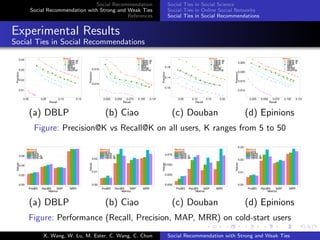
This document summarizes a paper on social recommendation with strong and weak ties. It begins by introducing social recommendation and techniques like rating prediction and top-N item recommendation. It then discusses how social ties have been studied in social science, defined in online social networks, and how they can be incorporated into recommendation models. Specifically, it presents methods to classify social ties as strong or weak based on metrics like Jaccard's coefficient. It also categorizes items based on whether they were consumed by a user's strong ties, weak ties, or neither, and proposes models like TBPR that integrate this social tie information to improve recommendations.



![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Social Rating Networks
Social network, where users are associated with item ratings.
Item ratings can be numeric [1..5]
or Boolean (bookmark url, like article, watch TV series . . .).
Social action: create social relationship, rating action: rate an
item.
Martin Ester: Recommendation in Social Networks, Tutorial at RecSys 2013
13
Social Rating Networks
0.8
0.7
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-4-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Matrix Factorization
Rating Prediction
A matrix factorization model [6] assumes the rating matrix R can
be approximated by a multiplication of d-rank factors,
R ≈ PT
Q, (1)
where P ∈ Rd×|U| and Q ∈ Rd×|I|. Normally d is far less than
both |U| and |I|. Thus given a user u and an item i, the rating
Rui of u for i can be approximated by the dot product of user
latent feature vector Pu and item latent feature Qi ,
Rui ≈ PT
u Qi = Pu, Qi , (2)
where Pu ∈ Rd×1 is the uth column of P and Qi ∈ Rd×1 is the ith
column of Q.
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-5-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Probabilistic Matrix Factorization
Rating Prediction
Social Networks, Tutorial at RecSys 2013
46
el based approaches
at minimize
)()
222
),
VURR ui
iu
ui ++− λ
)
ks, Tutorial at RecSys 2013
47
SoRec
a et al. 2008]
n model
gs and links together.
a binary matrix.
or items.
for users:
or,
er.
or both contexts (rating
actions). Martin Ester: Recommendation in Social Networks, Tutorial at RecSys 2013
50
Social Trust Ensemble
• Graphical model
Martin Ester: Recommendation in Social Networks, Tutorial at RecSys 2013
SocialMF
)((((
)()(
,,
222
),(
v
vvuu
v
vvu
u
u
ui
iuobservedall
ui
UTUUTU
VURR
∑∑∑
∑
−−+
++−
β
λ
)
(a) PMF[9] (b) SoRec[8] (c) STE[7] (d) SMF[5]
Figure: Graphical Models of Several Social Recommendation Models
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-6-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Bayesian Personalized Ranking (BPR)
Top-N Item Recommendation
BPR [10] categorizes items into two groups:
1 Consumed Items. For all u ∈ U, let Cself
u ⊆ I denote the set
of items consumed by u itself.
2 Non-Consumed Items. This category contains the rest of
the items (not consumed by u ): Cnone
u = {i : i ∈ I Cself
u }.
Clearly, for all u ∈ U, Cself
u ∪ Cnone
u = I.
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-7-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Intuitively, each user u should prefer the consumed items to
non-consumed items, i.e., the consumed items should be ranked
ahead of the non-consumed ones. Mathematically,
i u j, if i ∈ Cself
u ∧ j ∈ Cnone
u . (3)
The likelihood function can be expressed as:
L(Θ) =
u∈U i∈Cself
u
j∈Cnone
u
Pr[i u j] , (4)
where the probability that consumed items are preferred over
non-consumed items is as follows:
Pr[i u j] = δ(ˆxui − ˆxuj ) =
1
1 + exp(−(ˆxui − ˆxuj ))
=
1
1 + exp(− Pu, Qi + Pu, Qj )
.
(5)
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-8-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Social Bayesian Personalized Ranking (SBPR)
Top-N Item Recommendation
SBPR [11] categorizes items into three groups:
1 Consumed Items. For all u ∈ U, let Cself
u ⊆ I denote the set
of items consumed by u itself.
2 Social-Consumed Items. Any item i ∈ I Cself
u that has
been consumed by at least one of u’s social ties i.e., Tu,
belongs to this category. We denote this set by
Ctie
u = {i ∈ I Cself
u : ∃v ∈ Tu s.t. i ∈ Cself
v }
3 Non-Consumed Items. This category contains the rest of
the items (not consumed by u or any of u’s social ties):
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-9-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Rating Networks
Rating Prediction
Top-N Item Recommendation
Social Bayesian Personalized Ranking (SBPR)
Top-N Item Recommendation
With the new categorization, Social-Consumed Items are
assumed to lie between Consumed Items and Non-Consumed
Items for each user u :
i u j, if
i ∈ Cself
u ∧ j ∈ Ctie
u or
i ∈ Ctie
u ∧ j ∈ Cnone
u .
(6)
And the likelihood function is:
L(Θ) =
u∈U i∈Cself
u j∈Ctie
u
Pr[i u j]
j∈Ctie
u k∈Cnone
u
Pr[j u k] . (7)
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-10-320.jpg)

![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Getting a job: A study of contacts and careers
by Granovetter
Statements from Granovetter’s influential work [3, 2]:
Three different types of social ties, measured in terms of how
often they saw the contact person during the period of the job
transition:
Strong : at least once a week
Weak : more than once a year but less than twice a week
Absent : less than once a year
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-12-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Getting a job: A study of contacts and careers
by Granovetter
Statements from Granovetter’s influential work [3, 2]:
Three different types of social ties, measured in terms of how
often they saw the contact person during the period of the job
transition:
Strong : at least once a week
Weak : more than once a year but less than twice a week
Absent : less than once a year
Weak ties are actually the most important reason for new
information or innovations to spread over social networks.
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-13-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Getting a job: A study of contacts and careers
by Granovetter
Statements from Granovetter’s influential work [3, 2]:
Three different types of social ties, measured in terms of how
often they saw the contact person during the period of the job
transition:
Strong : at least once a week
Weak : more than once a year but less than twice a week
Absent : less than once a year
Weak ties are actually the most important reason for new
information or innovations to spread over social networks.
Late 1960s and early 1970s — no online social networks.
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-14-320.jpg)

![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Solutions
Social Ties in Online Social Networks
Utilizing features intrinsic to the network topology:
Jaccard’s Coefficient
Adamic-Adar
Katz score
In a recent work [1] on how strong ties and weak ties relate to job
finding on Facebook’s social network, Gee et.al use both mutual
interactions and node similarity (similar to Jaccard’s coefficient) to
measure tie strength and find results to be similar for both kinds of
measures, which provides support for using Jaccard’s coefficient as
tie strength measure.
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-16-320.jpg)
![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Jaccard’s Coefficient and Thresholding
Social Ties in Online Social Networks
Jaccard’s Coefficient [4]:
strength(u, v) =def
|Nu ∩ Nv |
|Nu ∪ Nv |
(Jaccard), (8)
where Nu ⊆ U (resp. Nv ⊆ U) denotes the set of ties of u
(resp. v).
For a given social network graph G, let θG ∈ [0, 1) denote the
threshold of tie strength such that
(u, v) is
strong, if strength(u, v) > θG;
weak, if strength(u, v) ≤ θG.
(9)
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-17-320.jpg)


![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Likelihood Function
Social Ties in Social Recommendations
L(Θ) =
u∈U i∈Cself
u j∈C
joint
u
Pr[i u j]
j∈C
joint
u
w∈Cweak
u
Pr[j u w]
w∈Cweak
u s∈C
strong
u
Pr[w u s]
s∈C
strong
u
k∈Cnone
u
Pr[s u k] , (12)
where for instance, the probability that consumed items are
preferred over JTC items can be written as follows.
Pr[i u j] = δ(ˆxui − ˆxuj ) =
1
1 + exp(−(ˆxui − ˆxuj ))
=
1
1 + exp(− Pu, Qi + Pu, Qj )
.
(13)
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-20-320.jpg)

![Social Recommendation
Social Recommendation with Strong and Weak Ties
References
Social Ties in Social Science
Social Ties in Online Social Networks
Social Ties in Social Recommendations
Incorporating the Tie Strength Threshold
Social Ties in Social Recommendations
To incorporate the threshold into the objective function so that our
TBPR model is able to learn it in a principled manner, we add a
coefficient 1/g(θG) into the probability that WTC items are
preferred over STC items. More specifically, we define:
Pr[w u s] = δ
ˆxuw − ˆxus
1 + 1/g(θG)
=
1
1 + exp − ˆxuw −ˆxus
1+1/g(θG )
=
1
1 + exp − Pu,Qw + Pu,Qs
1+1/g(θG )
, (15)
where we use 1 + 1/g(θG) to discount (ˆxuw − ˆxus), the difference
between u’s predicted score for w and s. The intuition is that, if
the current threshold θG does not separate the strong and weak
ties well enough, the likelihood that user prefers w (an WTC item
given the current threshold) to s (an STC items given the current
threshold) should be discounted.
X. Wang, W. Lu, M. Ester, C. Wang, C. Chun Social Recommendation with Strong and Weak Ties](https://image.slidesharecdn.com/cikm2016slides-170421054129/85/Social-Recommendation-with-Strong-and-Weak-Ties-22-320.jpg)