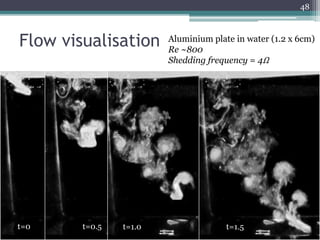
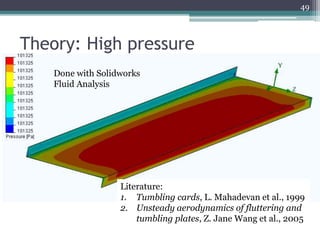
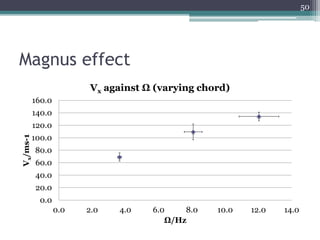
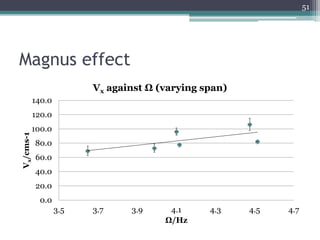
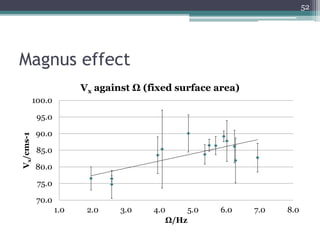
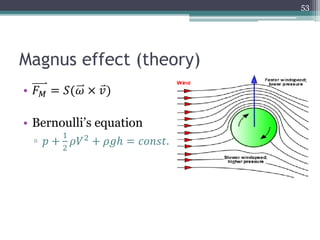
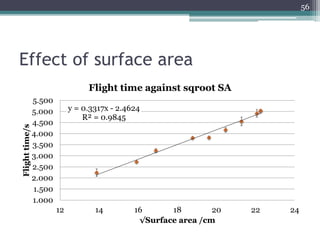
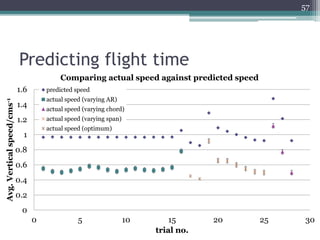
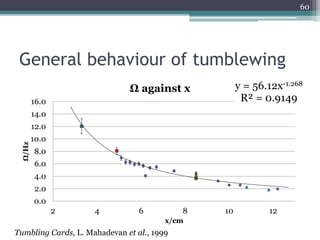
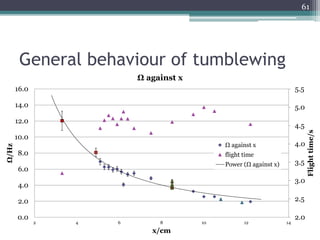
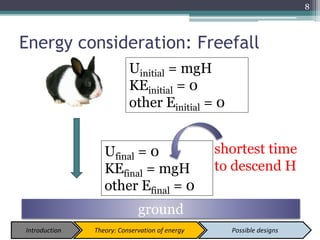
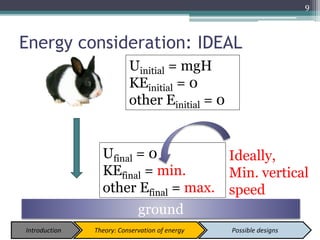
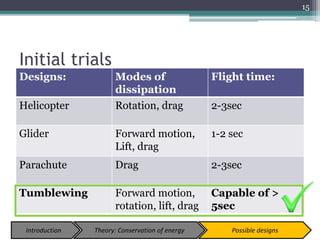
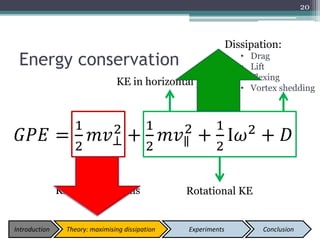
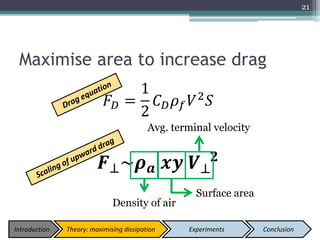
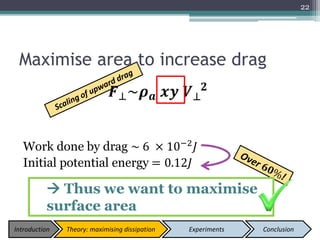
The document describes experiments to design a paper device that falls slowly through the air. It summarizes that a tumblewing design, which rotates and moves horizontally, works best by maximizing surface area for drag. Testing showed flight time increased with higher aspect ratio around 4.5, smaller edge width, and moderate launch angles between 10-60 degrees. The optimum design had an aspect ratio of 4.1, surface area of 573.5 cm^2, and edge width of 0.5 cm, achieving a maximum flight time of 6.5 seconds.

1. Q15. SLOW DESCENT
International Young Physicists’
Tournament 2011
Republic of Singapore
Zhang Nuda

2. Overview
2
Introduction
• Interpretation of question
• Preliminary data
Theory
• Conservation of energy
• Possible designs

3. Content: Chosen design
Theory
• How it works
• Energy dissipation model
Experiments
• Factors affecting flight time
• Making the best device
Conclusions
• Characteristics of optimum device
3

4. Question 15:
• Design and make a device, using one sheet of A4
80-gram-per-square-metre paper that will take
the longest possible time to fall to the ground
through a vertical distance of 2.5 m. A small
amount of glue may be used.
• Investigate the influence of various parameters.
4
Introduction Theory: Conservation of energy Possible designs

5. Interpretation of question
• “… make a device, using one sheet of A4 80 gsm
paper…”
▫ Must consume entire paper
▫ Can cut into different pieces but entire paper is put
together
• “… longest possible time to fall to the ground…”
▫ Release from rest
▫ No assisted launch, e.g., throwing, etc
5
Introduction Theory: Conservation of energy Possible designs

6. Preliminary data
• Plain 80gsm A4 paper allow to fall
▫ Time to drop 2.5 m approx. 2.4±0.4 s
 A successful device must fall
slower than a piece of paper
6
Introduction Theory: Conservation of energy Possible designs

7. Falling paper
• Back and forth & from side-
to-side
▫ i.e. fluttering
• Rotates end over end
▫ i.e. tumbling
• Chaotic behavior
(A. Belmonte et al., 1998)
7
Introduction Theory: Conservation of energy Possible designs
flutter tumble

8. Energy consideration: Freefall
shortest time
to descend H
Uinitial = mgH
KEinitial = 0
other Einitial = 0
Ufinal = 0
KEfinal = mgH
other Efinal = 0
8
ground
Introduction Theory: Conservation of energy Possible designs

9. ground
Energy consideration: IDEAL
Uinitial = mgH
KEinitial = 0
other Einitial = 0
Ufinal = 0
KEfinal = min.
other Efinal = max.
Ideally,
Min. vertical
speed
9
Introduction Theory: Conservation of energy Possible designs

10. Energy considerations
• Possibly convert energy to:
▫ Rotational KE
▫ Horizontal motion
▫ Heat
• Introduction of upward forces
▫ Lift
▫ Drag
10
Introduction Theory: Conservation of energy Possible designs

11. Possible design: Paper helicopter
• Concepts:
▫ Rotation
▫ Drag
11
Introduction Theory: Conservation of energy Possible designs

12. Possible design: Flying wing/glider
• Concepts:
▫ Lift
▫ Drag
▫ Forward velocity
12
Introduction Theory: Conservation of energy Possible designs

13. Possible design: Parachute
• Concepts:
▫ Drag
13
Introduction Theory: Conservation of energy Possible designs

14. Possible design: Tumblewing
• Concepts
▫ Rotation
▫ Forward velocity
▫ Lift
▫ Drag
• Pros:
• Most modes of
dissipation
• Largest area for drag
14
Introduction Theory: Conservation of energy Possible designs

15. Introduction Theory: Conservation of energy Possible designs
Designs: Modes of
dissipation
Flight time:
Helicopter Rotation, drag 2-3sec
Glider Forward motion,
Lift, drag
1-2 sec
Parachute Drag 2-3sec
Tumblewing Forward motion,
rotation, lift, drag
Capable of >
5sec
15
Initial trials

16. 16
Optimising flight time
Introduction Theory: maximising dissipation Experiments Conclusion

17. y
x
e
Design
17
𝒜ℛ =
𝑦
𝑥
𝑆 = 𝑥𝑦
‘leading edge’
‘trailing edge’
Introduction Theory: maximising dissipation Experiments Conclusion

18. Flight
18

19. Theory: The Magnus Effect
19
Lift
Rotation
Translational
velocity
Traps air;
high pressure
o

20. Energy conservation
20
𝐺𝑃𝐸 =
1
2
𝑚𝑣⊥
2
+
1
2
𝑚𝑣∥
2
+
1
2
I𝜔2
+ 𝐷
KE in vertical axis
KE in horizontal plane
Rotational KE
Dissipation:
• Drag
• Lift
• Flexing
• Vortex shedding
Introduction Theory: maximising dissipation Experiments Conclusion

21. Maximise area to increase drag
𝐹 𝐷 =
1
2
𝐶 𝐷 𝜌 𝑓 𝑉2
𝑆
𝑭⊥~𝝆 𝒂 𝒙𝒚 𝑽⊥
𝟐
21
Avg. terminal velocity
Density of air
Surface area
Introduction Theory: maximising dissipation Experiments Conclusion

22. Maximise area to increase drag
𝑭⊥~𝝆 𝒂 𝒙𝒚 𝑽⊥
𝟐
Work done by drag ~ 6 × 10−2
𝐽
Initial potential energy = 0.12𝐽
22
 Thus we want to maximise
surface area
Introduction Theory: maximising dissipation Experiments Conclusion

23. Experimental design
• LEGO® launcher with quick release cable for
consistent unbiased release
• Conducted in enclosed room without winds
23
Introduction Theory: maximising dissipation Experiments Conclusion

24. [1] Effect of aspect ratio
• Independent variable: Aspect ratio y/x
• Dependent variable
▫ Flight time
• Constants:
▫ Area, xy (450±3)cm2
▫ Edge width (1.00±0.05)cm
▫ Mass (4.990±0.005)g
▫ Launch angle (45.0±0. 5)deg
24
x
y
3.0 4.1 4.5 5.0 6.2 8.0 10.0
11.0 11.7 12.1 12.9 13.9 14.9 16.0 17.2
Introduction Theory: maximising dissipation Experiments Conclusion

25. [1] Effect of aspect ratio
25
4.00
4.20
4.40
4.60
4.80
5.00
5.20
1.0 6.0 11.0 16.0
Flighttime/s
Aspect ratio
Flight time against AR
Introduction Theory: maximising dissipation Experiments Conclusion

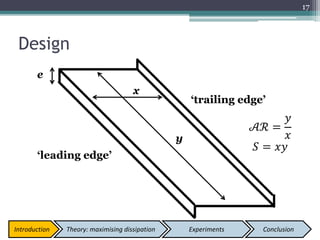
26. • Variable: edge width, e
▫ 0.3 0.6 0.9 1.0 1.2 1.5 1.8 2.1cm
• Constants:
▫ Span, y (45.00±0.05)cm
▫ Chord, x (10.00±0.05)cm
▫ Launch angle (45.0±0. 5)deg
• Assumption:
▫ Change in mass will not affect
flight time
[2] Effect of edge width
26
e
x
y
Introduction Theory: maximising dissipation Experiments Conclusion

27. [2] Effect of edge width
27
3.00
3.50
4.00
4.50
5.00
5.50
6.00
0.0 0.5 1.0 1.5 2.0 2.5
Flighttime/s
Edge width /cm
Flight time against edge width
Introduction Theory: maximising dissipation Experiments Conclusion

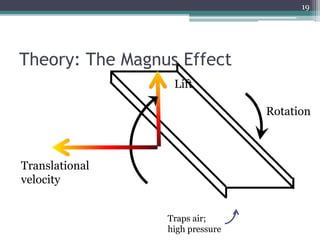
28. [3] Effect of launch angle
• Variable: Launch angle θ
▫ 0 – 120deg, at 10deg intervals
• Dependent variable:
▫ time
• Constants:
▫ Span, y (45.00±0.05)cm
▫ Chord, x (10.00±0.05)cm
▫ Edge width (1.00±0.05)cm
28
θ
Direction of flight
Introduction Theory: maximising dissipation Experiments Conclusion

29. [3] Effect of launch angle
29
Introduction Theory: maximising dissipation Experiments Conclusion
“Dead
Zone”
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
0.0 20.0 40.0 60.0 80.0
Flighttime/s
θ/deg
Flight time against launch angle

30. [4] The best tumblewing
• Characteristics:
▫ AR of 4.5
▫ Maximum surface area
▫ Small edge width
▫ Moderate launch angle
• Optimum model:
30
Span/cm Chord/cm AR SA/cm2 Edge/cm
48.6 11.8 4.1 573.5 0.5
Introduction Theory: maximising dissipation Experiments Conclusion

31. [4] The best tumblewing
31
2.00
2.50
3.00
3.50
4.00
4.50
5.00
5.50
6.00
6.50
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Flighttime/s
Wing no.
Comparing flight times optimum
varying aspect ratio
varying chord
varying span
Introduction Theory: maximising dissipation Experiments Conclusion

32. Conclusion
• Device with longest flight time: Tumblewing
▫ Rotation
▫ Forward velocity
▫ Lift
▫ Drag
 Makes maximum use of drag as entire area
of paper is exposed.
32
Introduction Theory: maximising dissipation Experiments Conclusion

33. Conclusion
• Flight time determined by:
▫ Surface area
 The larger the better
▫ Aspect ratio
 Best AR = 4.5
▫ Edge width
 As small as possible
▫ Launch angle
 Moderate angle between 10-60deg
33
Introduction Theory: maximising dissipation Experiments Conclusion

34. Thank you
34

35. [blank]
35

36. [blank]
36

37. [blank]
37

38. Possible designs
Concepts: (1) Rotation
(2) drag
Pro
• Stable due to rotation
Con
• Hard to scale to A4
• Long wingspan - flimsy
Paper helicopter
38

39. Possible designs
Concepts: (1) Lift
(2) drag
(3) forward velocity
Pro
• Large surface area for drag &
lift
• Dihedral wings can ensure
stability
Con
• Stall state when dropped
from rest
Flying
wing/glider
39

40. Possible designs
Concepts: (1) drag
Pro
• Maximum use of drag
Con
• Paper parachute is top
heavy  flips over
parachute
40

41. Concepts: (1) Rotation
(2) forward velocity
(3) Lift
(4) Drag
Possible designs
Pro
• Most modes of dissipation
• Large area for drag
Con
• Very flimsy
tumblewing
41

42. Expt. details: helicopter
•Approx. 70% of paper as blades
•Varied angle of attack and
measure flight time
•Timing increases over falling
paper by 10 – 20%
Angle of attack / o Time in air / s
0 2.30 ± 0.13
7 2.71 ± 0.13
10 2.91 ± 0.13
15 2.85 ± 0.13
20 2.81 ± 0.13
2.0
2.2
2.4
2.6
2.8
3.0
0 20
Timeinair/s
α / °

43. Expt. details: glider
• 15 models of paper gliders with initial launching
angles 0̊, 20̊, 40̊, 60̊ and 80̊.
• Bank and pitch corrections made via ailerons
and elevators.
43
 Flight times barely
exceed 2sec

44. Expt. details: parachute
44
Parachute Avg time: 2.28s
Blunt head Avg time: 2.58s

45. Measurements & calculations
• Flight time
• Tumbling frequency, Ω
• Horizontal velocity, 𝑉∥
• Vertical velocity, 𝑉⊥
• Energy lost via dissipation = 𝑀𝑔ℎ −
1
2
𝐼𝜔2
−
1
2
𝑀𝑉∥
2
−
1
2
𝑀𝑉⊥
2
• Reynolds number =
𝜌 𝑓Ω𝑥2
𝜇
(Mahadevan et al., 1999)
▫ Re ranged between 1000 -2000
45
Introduction Theory: maximising dissipation Experiments Conclusion

46. Launcher
46

47. Vorticity
• Kármán vortex street (R. Mittal et al., 2003)
▫ Periodic vortex shedding
• Strength and frequency of vortex shedding and
rotation rate interacts in complex and unknown
manners.
47

48. Flow visualisation
48
Aluminium plate in water (1.2 x 6cm)
Re ~800
Shedding frequency = 4Ω
t=0 t=0.5 t=1.0 t=1.5

49. Theory: High pressure
49
Done with Solidworks
Fluid Analysis
Literature:
1. Tumbling cards, L. Mahadevan et al., 1999
2. Unsteady aerodynamics of fluttering and
tumbling plates, Z. Jane Wang et al., 2005

50. Magnus effect
50
0.0
20.0
40.0
60.0
80.0
100.0
120.0
140.0
160.0
0.0 2.0 4.0 6.0 8.0 10.0 12.0 14.0
Vx/ms-1
Ω/Hz
Vx against Ω (varying chord)

51. Magnus effect
51
0.0
20.0
40.0
60.0
80.0
100.0
120.0
140.0
3.5 3.7 3.9 4.1 4.3 4.5 4.7
Vx/cms-1
Ω/Hz
Vx against Ω (varying span)

52. Magnus effect
52
70.0
75.0
80.0
85.0
90.0
95.0
100.0
1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
Vx/cms-1
Ω/Hz
Vx against Ω (fixed surface area)

53. Magnus effect (theory)
• 𝐹 𝑀 = 𝑆(𝜔 × 𝑣)
• Bernoulli’s equation
▫ 𝑝 +
1
2
𝜌𝑉2
+ 𝜌𝑔ℎ = 𝑐𝑜𝑛𝑠𝑡.
53

54. Drag equation applied to tumblewing
Drag Equation: 𝐹 𝐷 =
1
2
𝐶 𝐷 𝜌 𝑓 𝑉2 𝑆
𝐹⊥ = −𝐴 𝜌 𝑓 𝑥𝑦 𝑉⊥
2
|𝑐𝑜𝑠𝜃|
0
𝜋
2
𝑐𝑜𝑠𝜃 𝑑𝜃
𝜋
2
= 0.64
𝑭⊥~𝝆 𝒇 𝒙𝒚𝑽⊥
𝟐
54
θ

55. Drag equation applied to tumblewing
𝐹⊥~𝜌 𝑓 𝑥𝑦𝑉⊥
2
𝑚𝑔~𝜌 𝑓 𝑥𝑦𝑉2
𝑽⊥~
𝒎𝒈
𝝆 𝒇 𝒙𝒚
𝟏
𝟐
𝒕 𝜶 𝒙𝒚
55

56. Effect of surface area
56
y = 0.3317x - 2.4624
R² = 0.9845
1.000
1.500
2.000
2.500
3.000
3.500
4.000
4.500
5.000
5.500
12 14 16 18 20 22 24
Flighttime/s
√Surface area /cm
Flight time against sqroot SA

57. Predicting flight time
57
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0 5 10 15 20 25 30
Avg.Verticalspeed/cms-1
trial no.
Comparing actual speed against predicted speed
predicted speed
actual speed (varying AR)
actual speed (varying chord)
actual speed (varying span)
actual speed (optimum)

58. Comparing skin & form drag
• 𝐹⊥ = 𝐴⊥ 𝜌 𝑥𝑦 𝑉2
▫ 𝐴⊥ = 4.1 ± 0.1
• 𝐹∥ = 𝐴∥ 𝜌 𝑥𝑦 𝑉2
▫ 𝐴∥ = 0.88 ± 0.03
(From Flutter to Tumble: Inertial Drag and Froude
Similarity in Falling Paper, A. Belmonte et al., 1998)
58

59. Small edge width indeed better
• For the optimum tumblewing 2 models were
actually tested.
59
Edge width AR Flight time
1.0 cm 4.5 5.546 ± 0.008
0.5 cm 4.1 6.049 ± 0.008

60. General behaviour of tumblewing
60
y = 56.12x-1.268
R² = 0.9149
0.0
2.0
4.0
6.0
8.0
10.0
12.0
14.0
16.0
2 4 6 8 10 12
Ω/Hz
x/cm
Ω against x
Tumbling Cards, L. Mahadevan et al., 1999

61. 61
General behaviour of tumblewing
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
0.0
2.0
4.0
6.0
8.0
10.0
12.0
14.0
16.0
2 4 6 8 10 12 14
Flighttime/s
Ω/Hz
x/cm
Ω against x
Ω against x
flight time
Power (Ω against x)

62. Properties of A4 paper
Property Values
Mass: 4.990 x 10-3 kg
Dimensions: 0.211m by 0.298 m
(0.0629m2)
Volume: 6.917 x 10-6 m2
Density 730 kg·m-3
62

63. Data sheet
rho_air (kg m-3) 1.1644
mu_air (kg m-1 s-1) 1.98E-05
mass of paper (kg) =
0.00499
initial mgh 0.12238
mgh error 0.000367
thickness 0.00011
MOI (kg m2) 10−6
63