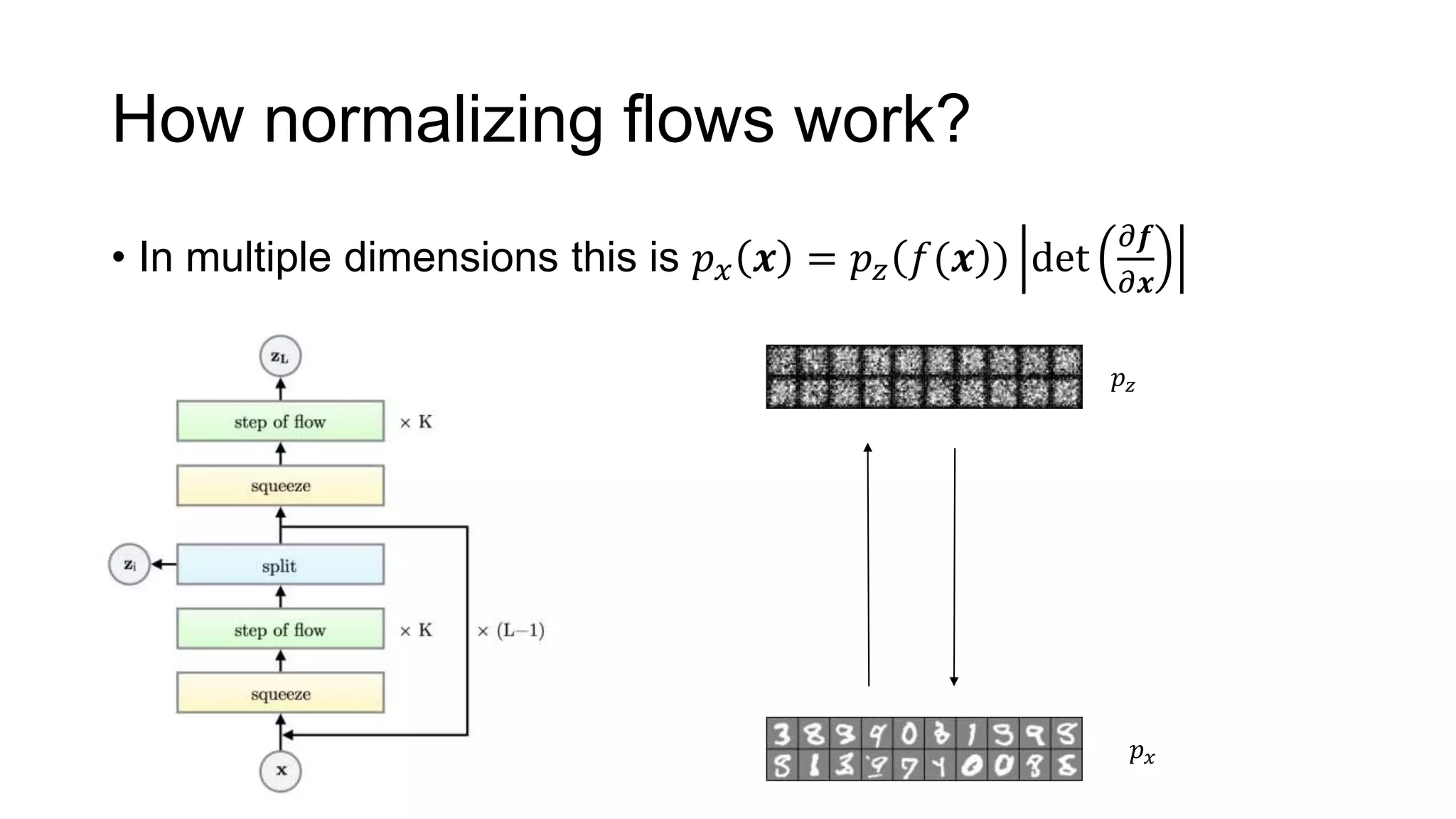
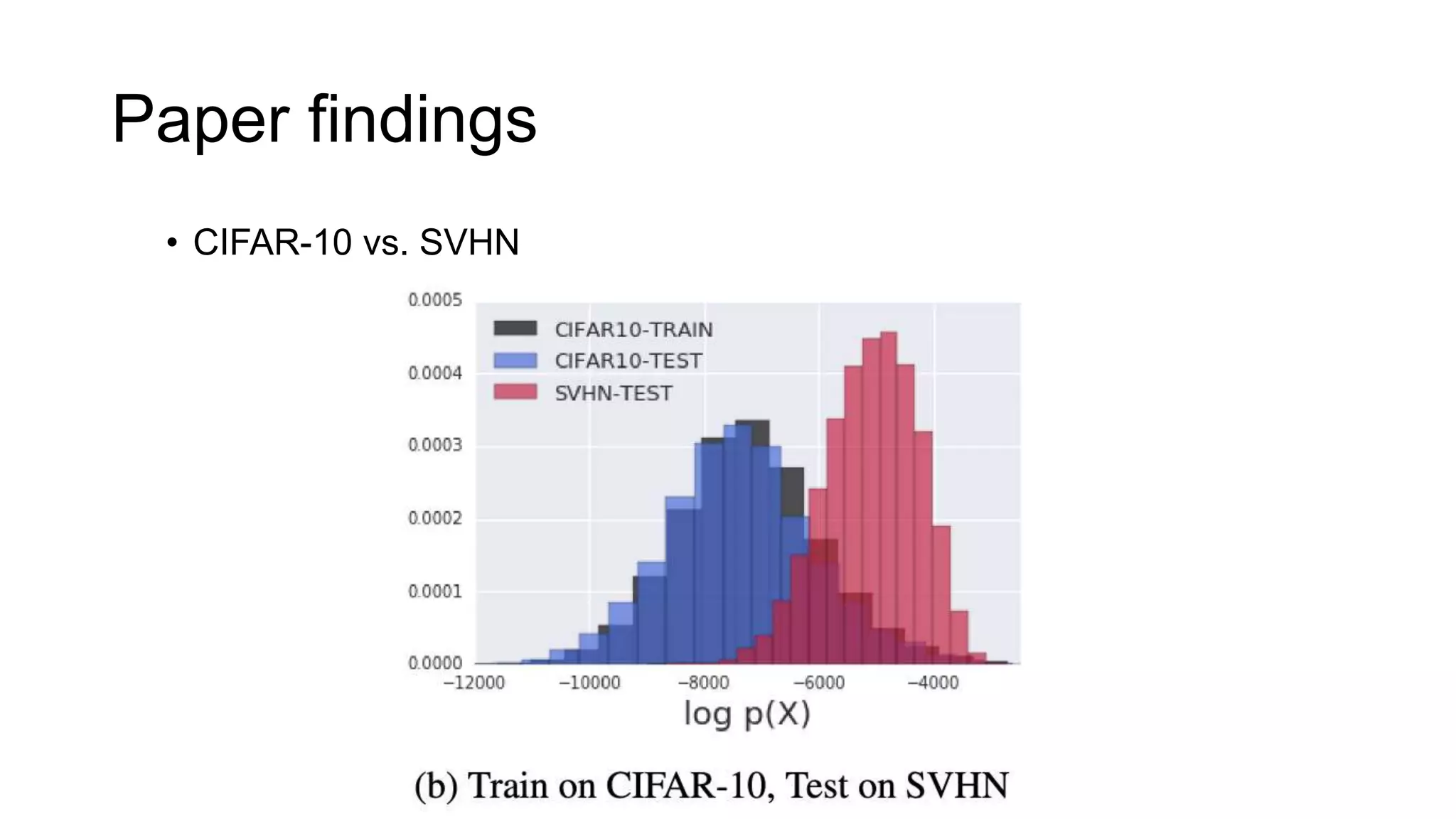
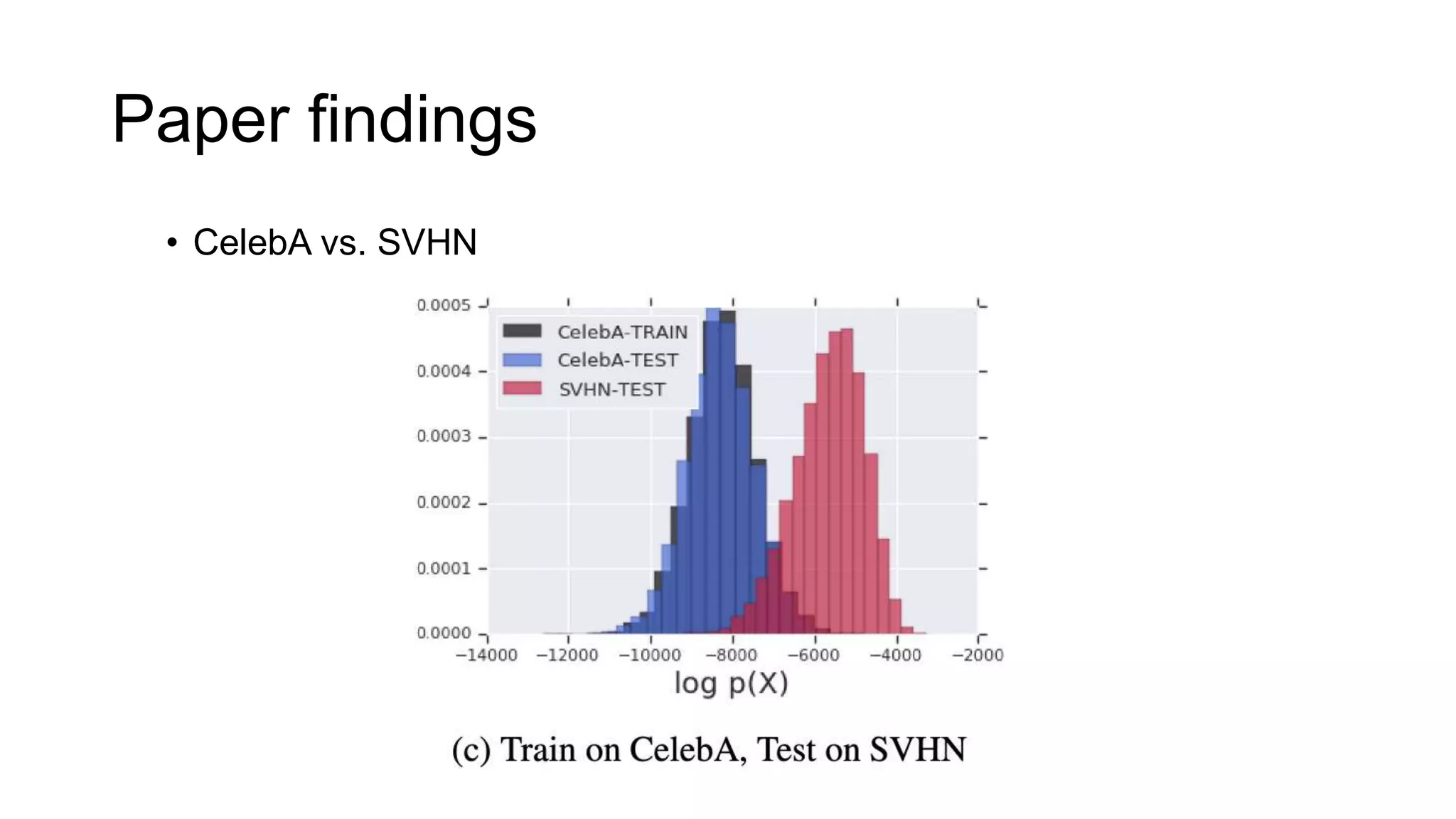
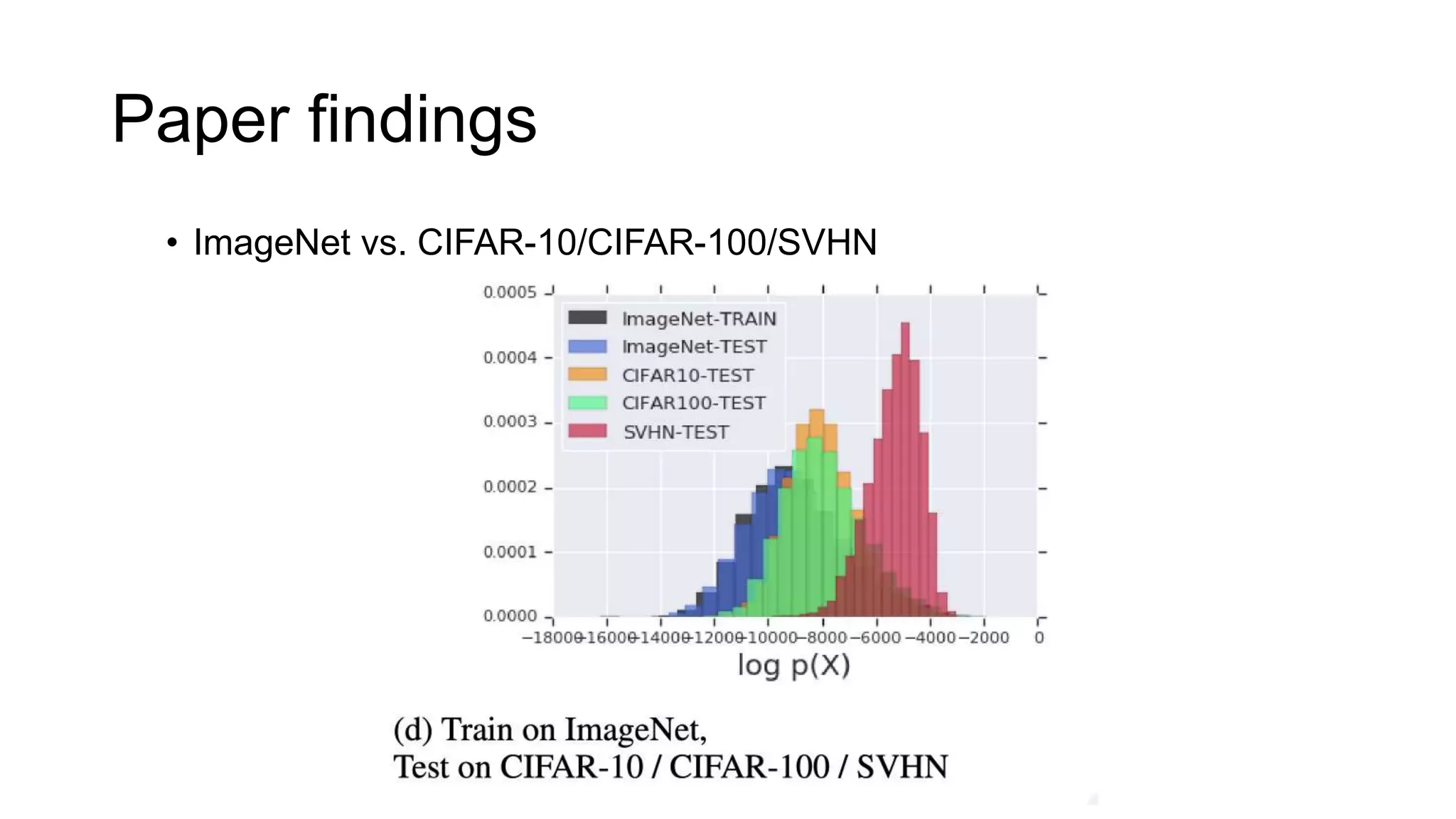
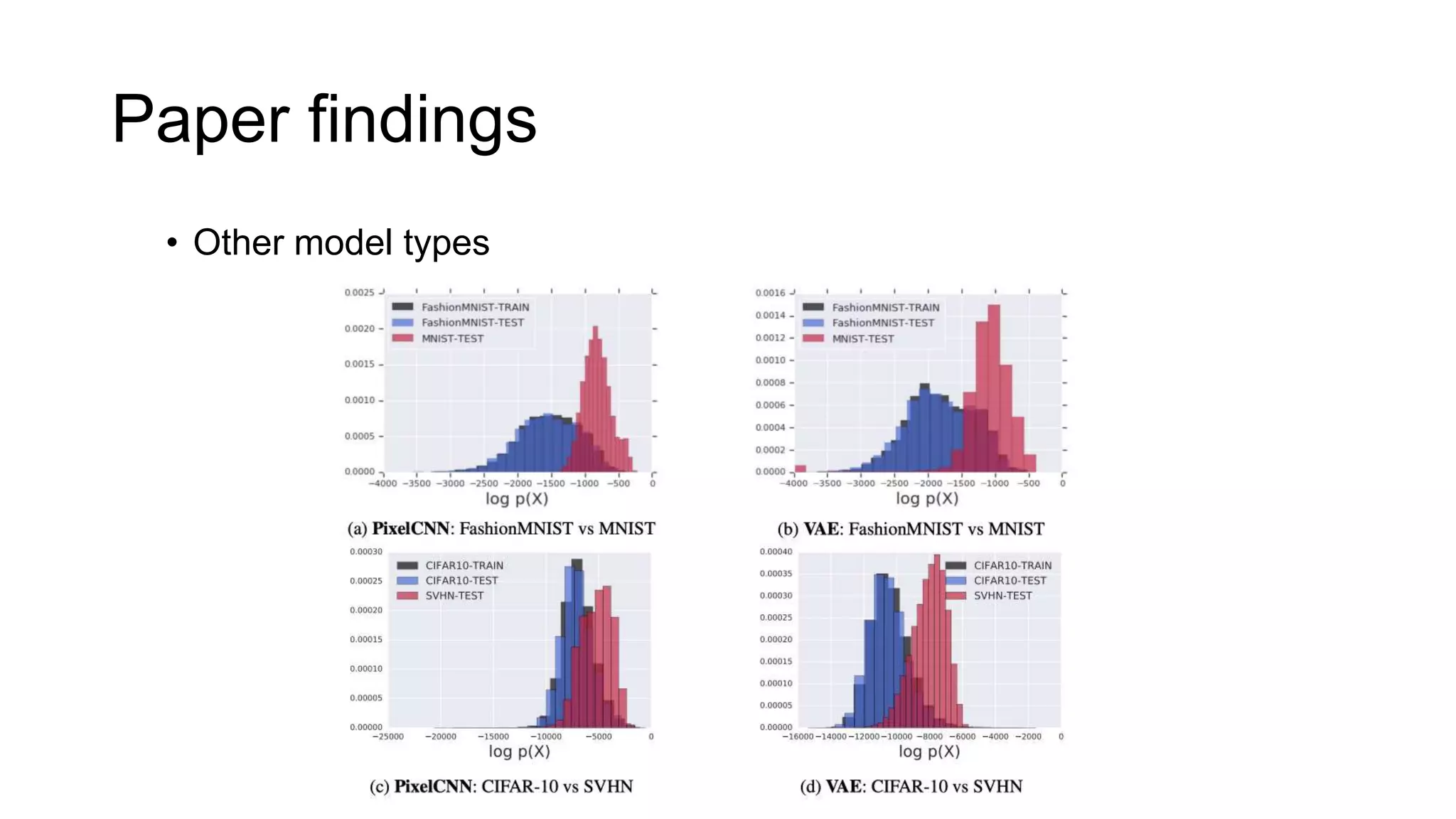
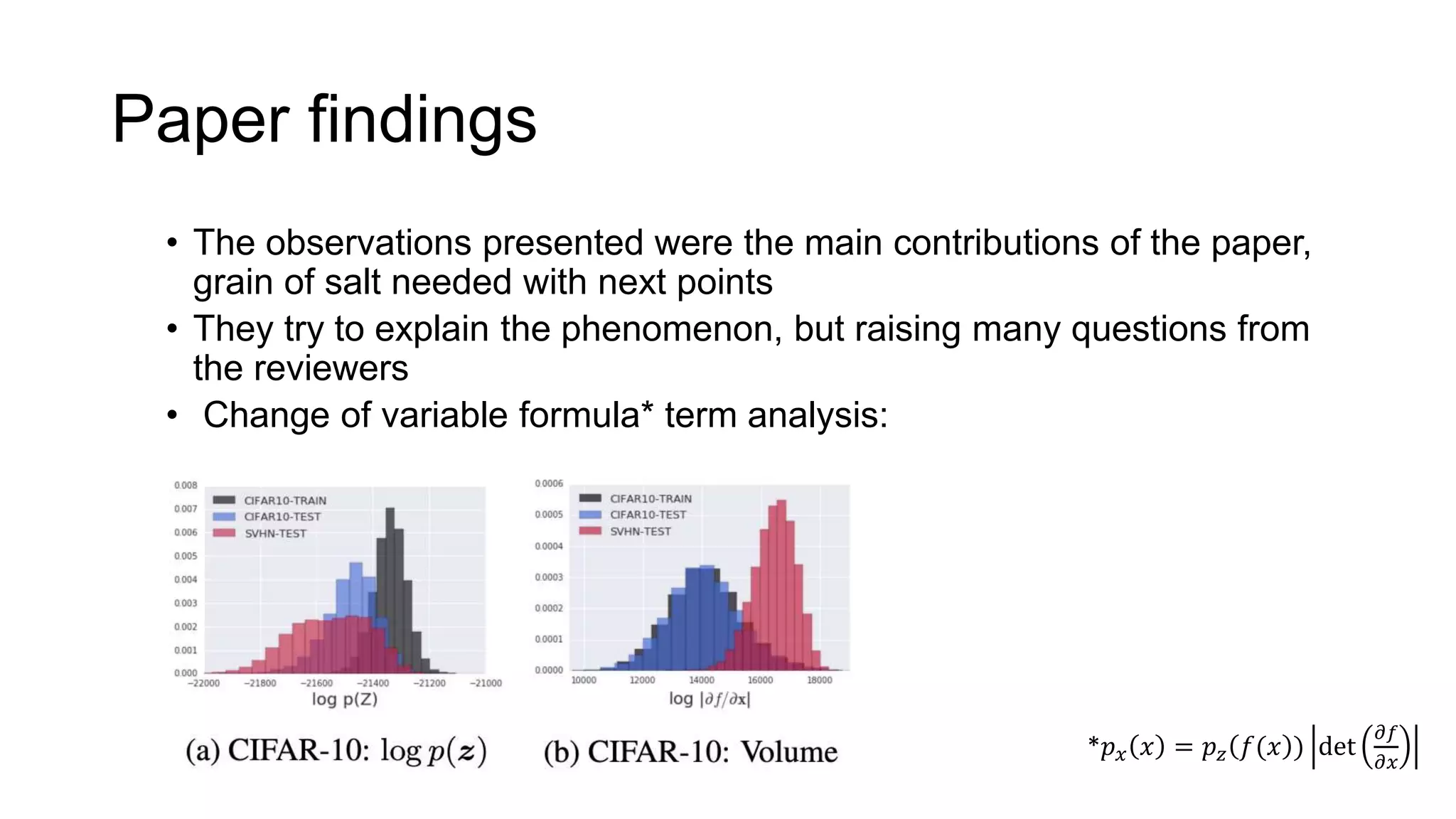
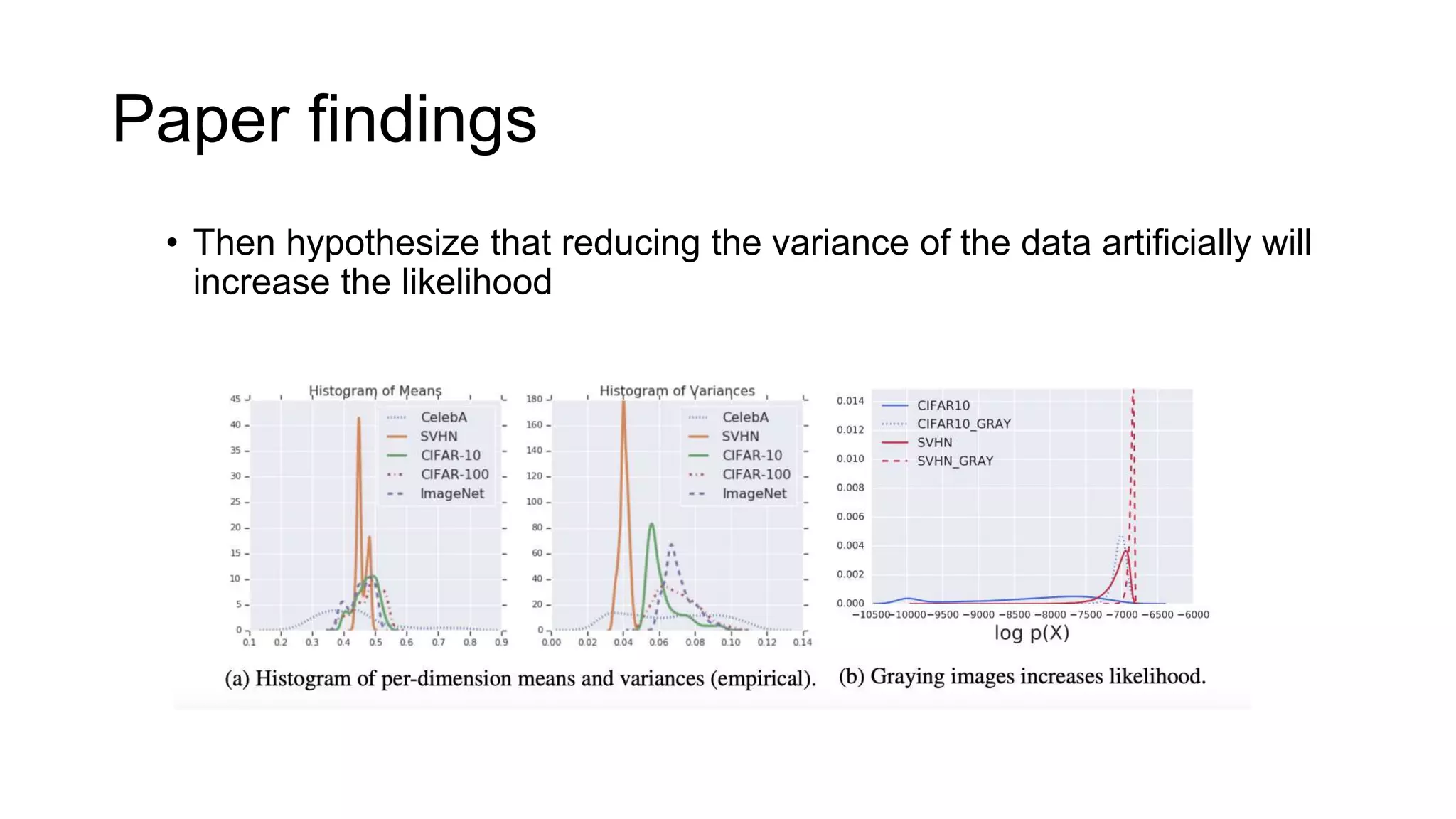
The paper examines the reliability of deep generative models, particularly normalizing flows, in detecting out-of-distribution data, raising concerns about their effectiveness in anomaly detection. The authors conduct experiments comparing several datasets and find that high likelihoods can occur for out-of-distribution data, which may lead to misleading results. The findings suggest a need for caution and further investigation regarding the use of generative models in this context.