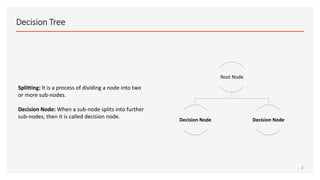
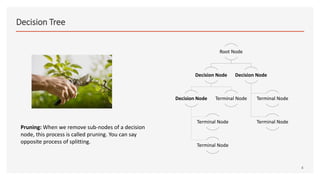
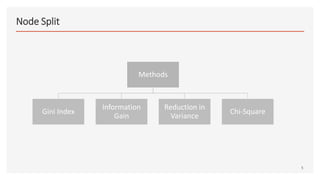
This document provides an overview of decision trees, including the key components and concepts. It defines the root node, decision nodes, terminal nodes, branches, and the relationships between parent and child nodes. It describes the processes of splitting nodes and pruning trees. Finally, it explains several common methods for splitting nodes, including Gini index, information gain, reduction in variance, and chi-square.

1. Decision Tree
1
Root Node
Root Node: It represents entire population or
sample and this further gets divided into two or
more homogeneous sets.

2. Decision Tree
2
Root Node
Decision Node Decision Node
Splitting: It is a process of dividing a node into two
or more sub-nodes.
Decision Node: When a sub-node splits into further
sub-nodes, then it is called decision node.

3. Decision Tree
3
Root Node
Decision Node
Decision Node
Terminal Node
Terminal Node
Terminal Node
Decision Node
Terminal Node
Terminal Node
Leaf/ Terminal Node: Nodes do not split is called
Leaf or Terminal node.
Branch / Sub-Tree: A sub section of entire tree is
called branch or sub-tree.
Parent and Child Node: A node, which is divided into
sub-nodes is called parent node of sub-nodes where
as sub-nodes are the child of parent node.

4. Decision Tree
4
Root Node
Decision Node
Decision Node
Terminal Node
Terminal Node
Terminal Node
Decision Node
Terminal Node
Terminal Node
Pruning: When we remove sub-nodes of a decision
node, this process is called pruning. You can say
opposite process of splitting.

5. Node Split
5
Methods
Gini Index
Information
Gain
Reduction in
Variance
Chi-Square

6. Gini Index - Formula
6
Gini Index = 1 – P2(Class 1) – P2(Class 2) - … - P2(Class N)
Or

7. Gini Index - Example
Target Count %
Yes 346 74%
No 124 26%
Total 470 100%
Gini Index = 1 - 0.742 - 0.262
= 1-0.5476 -0.0676
= 0.3848

8. Entropy
• Which node can be described easily ?
• Which is purest group ?

9. Entropy
9
Entropy = - p log2 p – q log2 q
If the sample is completely
homogeneous the entropy is zero
and if the sample is an equally
divided it has entropy of one.
Degree of disorganization in a system

10. Entropy - Example
10
Play Golf
Yes No
Outlook
Sunny 3 2 5
Overcast 4 0 4
Rainy 2 3 5
9 5 14
Entropy (Play Golf, Outlook) = 5/14 * [ - 3/5 log 3/5 – 2/5 log 2/5] + 4/14 [ - 4/4 log 4/4] + 5/14 [- 2/5 log 2/5 – 3/5 log
3/5]
= 0.46 * 0.971 + 0.28 * 0.0 + 0.56 * 0.971
= 0.693
Entropy (Play Golf) = Entropy (9/14, 5/14)
= - 9/14 log 9/14 – 5/14 log 5/14
= 0.95

11. Information Gain
• Decrease in randomness
• Decrease in entropy
• More information
• More homogeneity

12. Reduction in Variance
1. Calculate variance for each node.
2. Calculate variance for each split as weighted average of each node
variance.

13. Chi-Square
• It works with categorical target
variable “Success” or “Failure”.
• It can perform two or more splits.
• Higher the value of Chi-Square
higher the statistical significance
of differences between sub-node
and Parent node.
• Chi-Square of each node is
calculated using formula, Chi-
square = ((Actual – Expected)^2 /
Expected)^1/2
• It generates tree called CHAID
(Chi-square Automatic Interaction
Detector)

14. Chi-Square
1.Calculate Chi-
square for individual
node by calculating
the deviation for
Success and Failure
both
1.Calculated Chi-
square of Split using
Sum of all Chi-square
of success and
Failure of each node
of the split