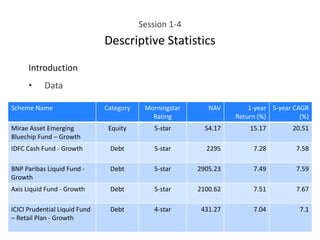
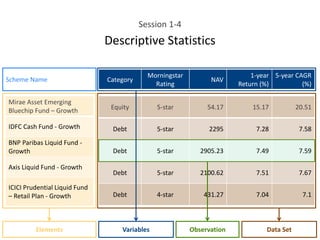
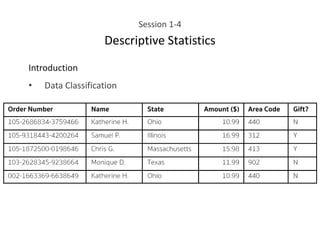
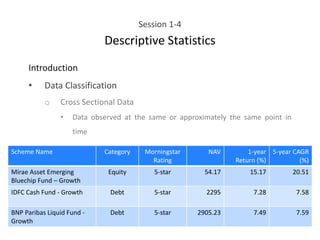
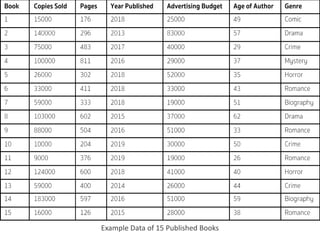
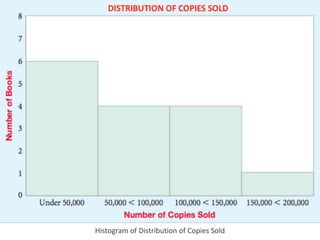
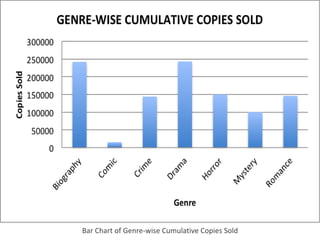
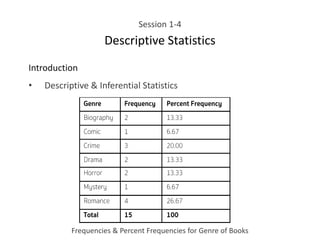
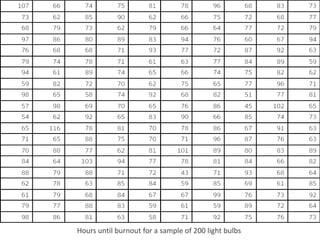
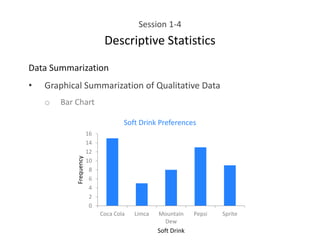
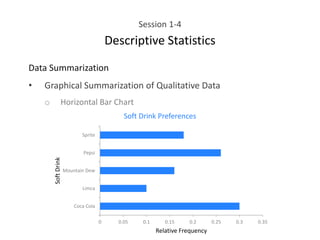
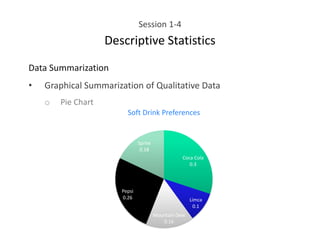
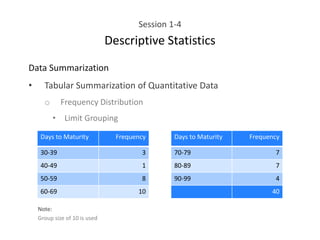
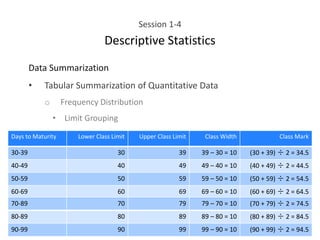
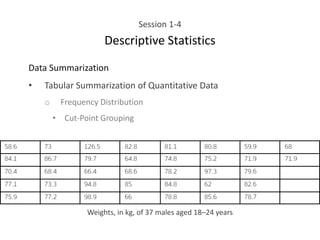
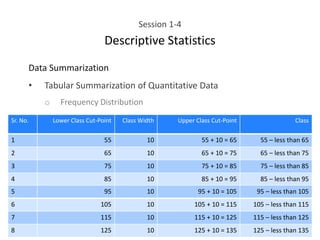
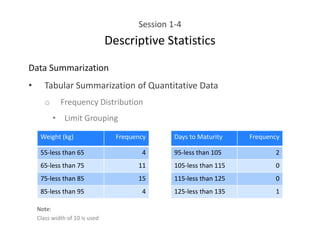
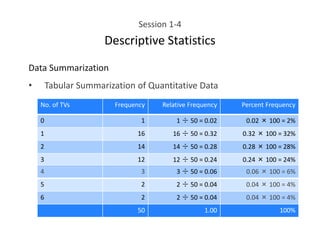
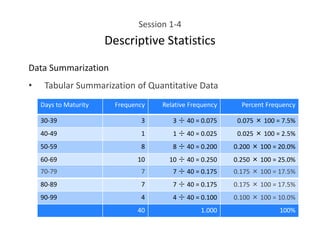
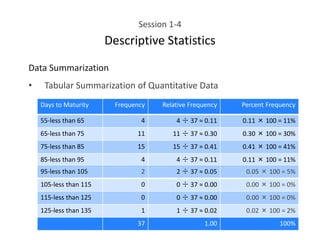
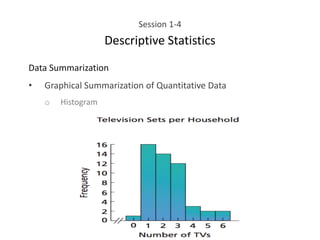
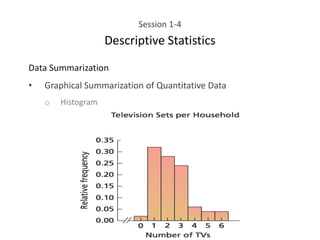
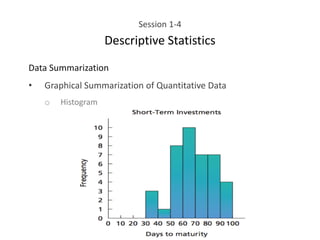
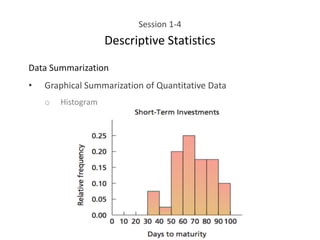
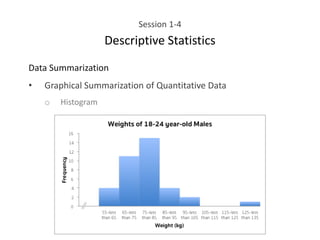
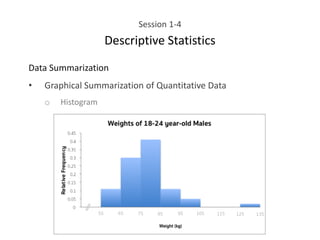
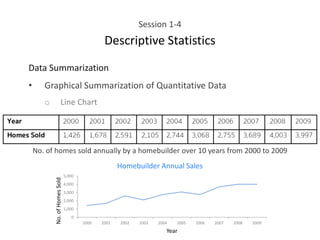
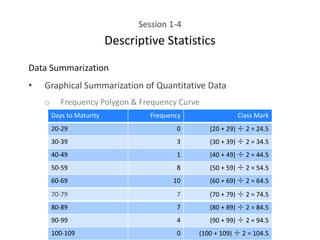
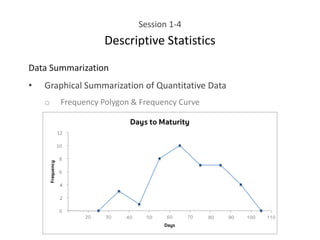
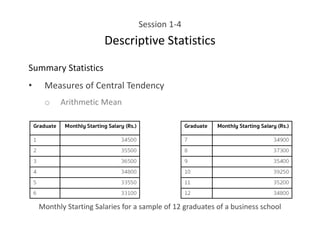
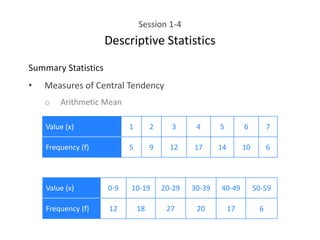
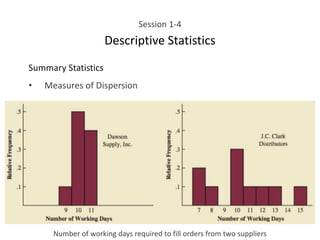
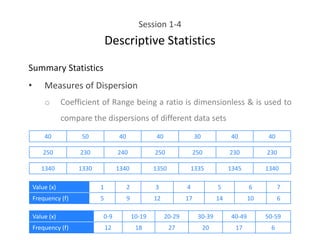
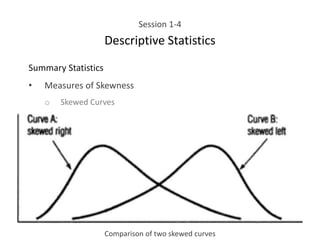
This document provides an overview of descriptive statistics concepts including data, scales of measurement, data classification, and descriptive versus inferential statistics. It discusses how qualitative and quantitative data can be summarized numerically through measures like mean and variation, and visually through charts, graphs, and distributions. Tabular and graphical techniques for summarizing both qualitative and quantitative data are introduced.